
- •Министерство образования и науки российской федерации
- •ТюмГнгу
- •Введение
- •Общие требования к выполнению практических занятий
- •1 Порядок проведения занятий
- •2 Предварительная подготовка
- •3 Содержание отчета
- •Критерии оценки практических занятий
- •Практическое занятие №1 расчет спектра периодических сигналов
- •Теоретический материал
- •Практическое занятие №2 расчет и построение временных и спектральных диаграмм амплитудно-модулированных сигналов
- •Теоретический материал
- •Алгоритм выполнения
- •Практическое занятие №3 расчет и построение временных и спектральных диаграмм частотно-модулированных сигналов
- •Теоретический материал
- •Алгоритм выполнения
- •Практическое занятие №4 преобразование непрерывного сигнала в дискретный сигнал
- •Теоретический материал
- •Практическое занятие №5 квантование непрерывного сигнала
- •Теоретический материал
- •Практическое занятие №6 регенерация цифрового сигнала
- •Теоретический материал
- •Алгоритм выполнения
- •Контрольные вопросы
- •Сборник практических занятий
Практическое занятие №5 квантование непрерывного сигнала
Цель занятия: формирование навыков квантования непрерывного сигнала
Теоретический материал
Квантование
(англ. quantization) - в информатике разбиение
диапазона значений непрерывной или
дискретной величины на конечное число
интервалов. Существует также векторное
квантование - разбиение пространства
возможных значений векторной величины
на конечное число областей. Квантование
часто используется при обработке
сигналов, в том числе при сжатии звука
и изображений. Простейшим видом
квантования является деление целочисленного
значения на натуральное число, называемое
коэффициентом квантования. Однородное
(линейное) квантование - разбиение
диапазона значений на отрезки равной
длины. Его можно представлять как деление
исходного значения на постоянную
величину (шаг квантования) и взятие
целой части от частного:
![]() .
.

Рисунок 5.1- Квантованный сигнал

Рисунок 5.2-Неквантованный сигнал с дискретным временем
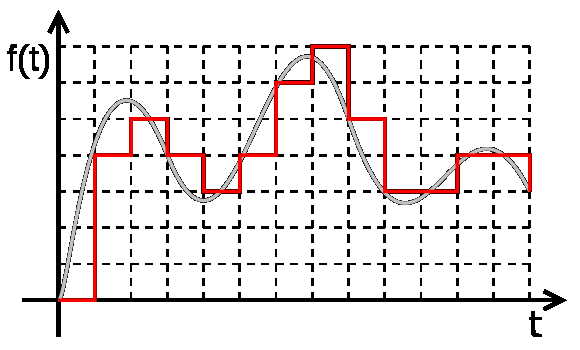
Рисунок 5.3 - Цифровой сигнал
Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации). При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике - по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть, разбивает по уровню сигнала (на графике - по вертикали). Сигнал, к которому применены дискретизация и квантование, называется цифровым. При оцифровке сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ 6 дБ).Квантование по уровню - представление величины отсчётов цифровыми сигналами. Для квантования в двоичном коде диапазон напряжения сигнала от Umin до Umax делится на 2n интервалов. Величина получившегося интервала (шага квантования):
![]() 5.1
5.1
Каждому интервалу присваивается n-разрядный двоичный код - номер интервала, записанный двоичным числом. Каждому отсчёту сигнала присваивается код того интервала, в который попадает значение напряжения этого отсчёта. Таким образом, аналоговый сигнал представляется последовательностью двоичных чисел, соответствующих величине сигнала в определённые моменты времени, то есть цифровым сигналом. При этом каждое двоичное число представляется последовательностью импульсов высокого (1) и низкого (0) уровня.
Алгоритм выполнения
Пример №1. Величина отсчета исходного сигнала в некоторый момент равна –238,2 мВ. Шаг квантования равен 2,5 мВ. Определить разрядность кода и кодовую группу, соответствующую этому отсчету, при использовании симметричного кода при равномерном квантовании. Решение:
Разрядность определяем по квантованному значению Uкв:
![]() мВ,
округляем до 95, так как код симметричный,
то может быть Uкв=±95
мВ.Число уровней квантования Nкв.
будет 190 (2Uкв
Для этого количества уровней m-разрядность
находится:
мВ,
округляем до 95, так как код симметричный,
то может быть Uкв=±95
мВ.Число уровней квантования Nкв.
будет 190 (2Uкв
Для этого количества уровней m-разрядность
находится:
![]() ;
;
![]() ;
;
![]() .
.
Так как Nкв. =190, то m=8.
Находим кодовую группу для квантованного значения +95. Пусть положительный отсчет кодируется как 1.
![]()
![]()
Находим кодовую группу для квантованного значения -95. Пусть отрицательный отсчет кодируется как 0.
![]()
![]() Пример
№2. На вход
декодера поступает кодовая группа,
записанная симметричным кодом 10111010.
Шаг квантования D=1,0 мВ. Определить
амплитуду АИМ-сигнала на выходе декодера.
Квантование равномерное. Решение:
Пример
№2. На вход
декодера поступает кодовая группа,
записанная симметричным кодом 10111010.
Шаг квантования D=1,0 мВ. Определить
амплитуду АИМ-сигнала на выходе декодера.
Квантование равномерное. Решение:
Первая посылка знаковая, пусть 1 положительный знак амплитуды АИМ-сигнала.
 мВ.
мВ.
Задание №1. Величина отсчета исходного сигнала в некоторый момент равна... U.(мВ). Шаг квантования равен .... d(мВ). Определить разрядность кода и кодовую группу, соответствующую этому отсчету, при использовании симметричного кода при равномерном квантовании.
Задание №2. На вход декодера поступает кодовая группа, записанная симметричным кодом ….. Шаг квантования d =1,0 мВ. Определить амплитуду АИМ-сигнала на выходе декодера. Квантование равномерное.
Таблица 5.1
Данные для выполнения заданий
|
№ варианта |
Задача 1, величина сигнала в мВ |
Задача 2, код |
|
1 |
U-150,d-1,5 |
10011010 |
|
2 |
U-170,d-1,7 |
00110011 |
|
3 |
U-250,d-2,5 |
00100010 |
|
4 |
U-180,d-1,5 |
10001000 |
|
5 |
U-150,d-1,5 |
11001100 |
|
6 |
U-120,d-2 |
10101010 |
|
7 |
U-150,d-1 |
01010101 |
|
8 |
U-240,d-2,4 |
01100110 |
|
9 |
U-200,d-2,0 |
11000011 |
|
10 |
U-170,d-1,7 |
00110011 |
|
11 |
U-250,d-2,5 |
00100010 |
|
12 |
U-180,d-1,5 |
10001000 |
|
13 |
U-150,d-1,5 |
11001100 |
|
14 |
U-120,d-2 |
10101010 |
|
15 |
U-150,d-1 |
01010101 |
|
16 |
U-240,d-2,4 |
01100110 |
|
17 |
U-200,d-2,0 |
11000011 |
|
18 |
U-230,d-2,3 |
10100011 |
|
19 |
U-170,d-1,7 |
00110011 |
|
20 |
U-250,d-2,5 |
00100010 |
|
21 |
U-180,d-1,5 |
10001000 |
|
22 |
U-150,d-1,5 |
11001100 |
|
23 |
U-120,d-2 |
10101010 |
|
24 |
U-150,d-1 |
01010101 |
|
25 |
U-240,d-2,4 |
01100110 |
|
26 |
U-200,d-2,0 |
11000011 |
|
27 |
U-230,d-2,3 |
10100011 |
|
28 |
U-170,d-1,7 |
00110011 |
|
29 |
U-250,d-2,5 |
00100010 |
|
30 |
U-180,d-1,5 |
10001000 |
Контрольные вопросы:
1.Какое преобразование сигнала называется квантованием?
2.Что такое шаг квантования?
3.Какие сигналы называются дискретными (цифровыми)?
4.Что называют ошибкой квантования (помехой квантования)?
