
- •«Тюменский государственный нефтегазовый университет»
- •Физика, часть 3
- •Волновая оптика
- •Световой вектор. Уравнение плоской световой волны
- •Интерференция световых волн. Условия, необходимые для осуществления интерференции
- •Условия максимумов и минимумов при интерференции световых волн
- •Интерференция в тонких пленках
- •Кольца Ньютона
- •Контрольные вопросы
- •Дифракция света. Принцип Гюйгенса-Френеля
- •Дифракция от одной щели.
- •Дифракция на одномерной дифракционной решётке
- •Угловая дисперсия и разрешающая способность дифракционной решетки
- •Угловая дисперсия равна:
- •Дифракция рентгеновских лучей на пространственной решетке
- •Поглощение света
- •Поляризация света. Естественный и поляризованный свет
- •1.Явления квантовой оптики
- •1.1. Тепловое излучение и его характеристики. Закон Кирхгофа
- •1.2.Законы излучения абсолютно черного тела. Законы Стефана-Больцмана и Вина
- •1.3.Формула Релея-Джинса. Ультрафиолетовая катастрофа. Квантовая гипотеза и формула Планка
- •1.4.Оптическая пирометрия
- •1.5.Квантовая природа света. Фотон и его характеристики.
- •1.6. Виды фотоэффекта. Внешний фотоэффект и его законы.
- •1.7. Эффект Комптона
- •1.8. Коpпускуляpно-волновой дуализм свойств света
- •1.9. Контрольные вопросы и задачи к разделу «Явления квантовой оптики»
- •2.Элементы квантовой механики
- •2.1. Гипотеза де Бройля. Корпускулярно-волновой дуализм микрочастиц
- •2.2. Соотношение неопределенностей
- •2.3. Волновая функция
- •2.4. Уравнение Шредингера
- •2.5.Задача квантовой механики о движении свободной частицы
- •2.6. Задача квантовой механики о частице в одномерной прямоугольной потенциальной яме
- •1. Пусть размер ямы соизмерим с размерами атома, то есть м. Тогда
- •2. Пусть размер ямы велик, то есть м (свободные электроны в металле). Тогда
- •2.7. Понятие о туннельном эффекте.
- •1.8. Атом водорода в квантовой механике. Квантовые числа
- •Здесь и совпадает с формулой радиуса первой боровской орбиты; численное значение этого параметра равно;a – множитель, который можно определить из условия нормировки волновой функции:
- •2.10. Спин электрона. Принцип Паули
- •2.11. Спектр атома водорода
- •2.12. Распpеделение электpонов в атоме по энеpгетическим состояниям. Пеpиодическая система элементов д.И.Менделеева
- •2.13. Рентгеновское излучение
- •2.14. Поглощение света, спонтанное и вынужденное излучения
- •2.15. Лазеры
- •1. Инверсия населенностей
- •2. 16. Способы создания инверсии населенностей
- •2.17. Положительная обратная связь. Резонатор
- •2.18. Принципиальная схема лазера
- •2.17. Линейный гаpмонический осциллятоp
- •3.6. Понятие о квантовой теории электропроводности металлов
- •3.7. Явление сверхпроводимости. Свойства сверхпроводников
- •Критические температуры перехода для некоторых сверхпроводников
- •4.Зонная теория твёрдых тел
- •4.1. Энергетические зоны электронов в кристалле
- •4.2. Металлы, полупроводники, диэлектрики в зонной теории твёрдых тел
- •4.3.Полупроводники. Собственная проводимость полупроводников
- •4.4. Примесная проводимость полупроводников
- •4.5. Равновесные концентрации носителей заряда в полупроводнике
- •4.6. Зависимость электропроводности полупроводников от температуры
- •Электронно-дырочный переход
- •Внутренний фотоэффект
- •Воздействие излучения на полупроводник. Фоторезистивный эффект
- •Устройство и характеристики фоторезисторов
- •Применение фоторезисторов
- •Фотоэффект в электронно-дырочном переходе. Фото-э.Д.С.
- •Применение вентильного фотоэффекта
- •Биполярный транзистор
- •Характеристики атомного ядра
- •Ядерные силы
- •Понятие об обменном характере ядерных сил. Кванты ядерного поля
- •Радиоактивность
- •Ядерные реакции
- •Деление атомных ядер
- •Элементарные частицы
- •2 Кристаллические решетки твердых тел представляют собой периодические структуры и являются естественными трехмерными дифракционными решетками.
4.5. Равновесные концентрации носителей заряда в полупроводнике
Рассмотрим собственный
полупроводник в условиях равновесия.
Обозначим символами:
![]() - концентрацию электронов,
- концентрацию электронов,
![]() - концентрацию дырок,
- концентрацию дырок,
![]() и
и
![]() -
эффективные массы электронов и дырок
соответственно.
-
эффективные массы электронов и дырок
соответственно.
Концентрация
электронов, энергия которых находится
в интервале
![]() ,
определится выражением:
,
определится выражением:
![]() .
(4.2)
.
(4.2)
В этом выражении:
![]() - вероятность заполнения энергетического
уровня,
- вероятность заполнения энергетического
уровня,
![]() - число квантовых состояний в единице
объёма в интервале энергий
- число квантовых состояний в единице
объёма в интервале энергий![]() .
Оно определится формулой:
.
Оно определится формулой:
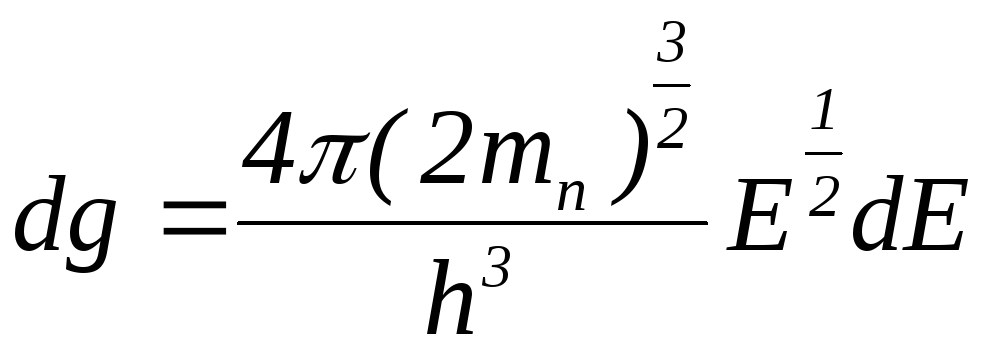 .
.
Вероятность заполнения электроном энергетического уровня определится функцией Ферми-Дирака
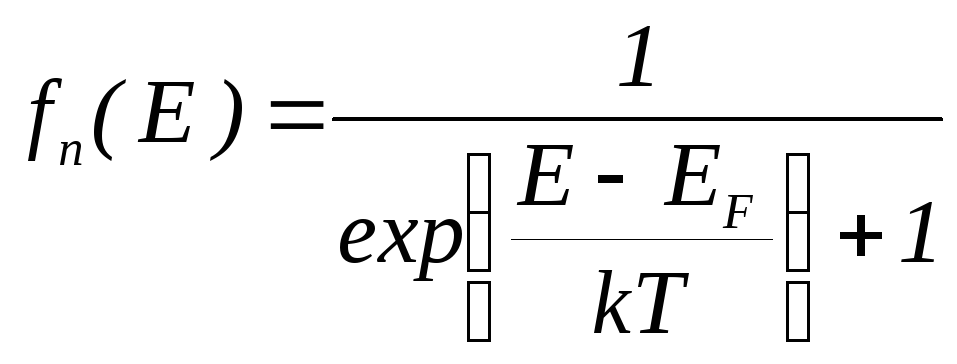 .
(4.3)
.
(4.3)
Вероятность того, что уровень не занят электроном будет равна:
![]() .
.
Если рассматривать
энергетические уровни вблизи потолка
валентной зоны, то
![]() - вероятность того, что энергетический
уровень занят дыркой.
- вероятность того, что энергетический
уровень занят дыркой.
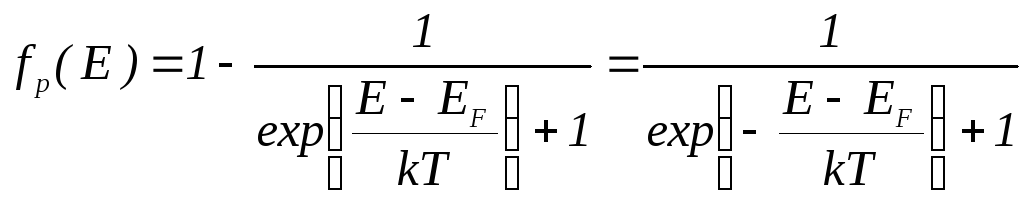 .
(4.4)
.
(4.4)
Так
как ширина запрещённой зоны в полупроводнике
![]() ,
то в знаменателе выражений (4.3) и (4.4)
можно пренебречь
единицей по сравнению
с экспоненциальным слагаемым. Тогда
выражения (4.3) и (4.4) приобретают вид:
,
то в знаменателе выражений (4.3) и (4.4)
можно пренебречь
единицей по сравнению
с экспоненциальным слагаемым. Тогда
выражения (4.3) и (4.4) приобретают вид:
![]()
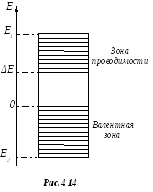 ,(4.5)
,(4.5)
![]() .(4.6)
.(4.6)
Из формул (4.5) и (4.6) следует, что электроны в полупроводнике подчиняются статистике Максвелла-Больцмана, то есть электронный газ в полупроводнике не вырожден.
Выберем за начало отсчёта энергии потолок валентной зоны (рис.4.14). Число энергетических состояний в нижней части зоны проводимости определится формулой:
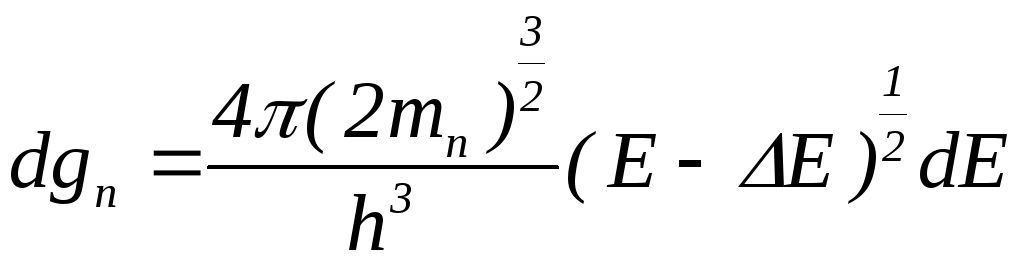 .
(4.7)
.
(4.7)
Подставим выражения (4.5) и (4.7) в (4.2), получим:
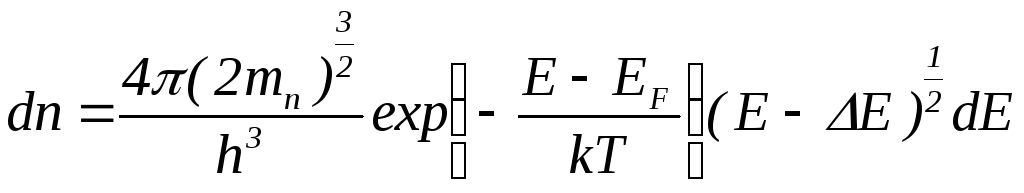 .
(4.8)
.
(4.8)
Концентрация электронов в зоне проводимости собственного полупроводника определится интегралом:
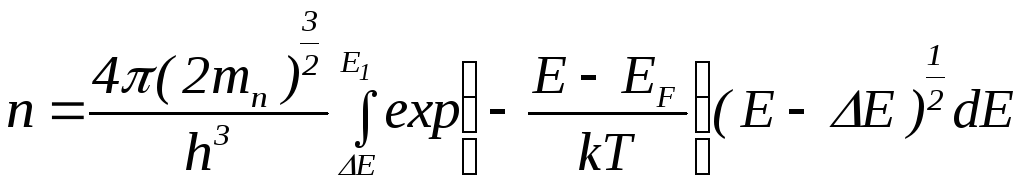 (4.9)
(4.9)
Произведём замену переменных
в уравнении (4.9):
![]() ,
,![]() ,
получим:
,
получим:
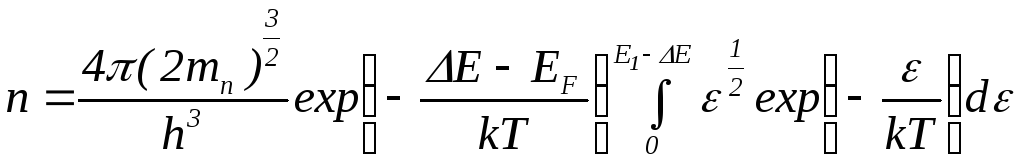 . (4.10)
. (4.10)
Рассмотрим интеграл в выражении (4.10). Так как вероятность заполнения верхних энергетических уровней зоны проводимости практически равна нулю, то верхний предел интегрирования можно заменить на ∞. Тогда
![]() ,
(4.11)
,
(4.11)
и концентрация электронов в зоне проводимости определится выражением:
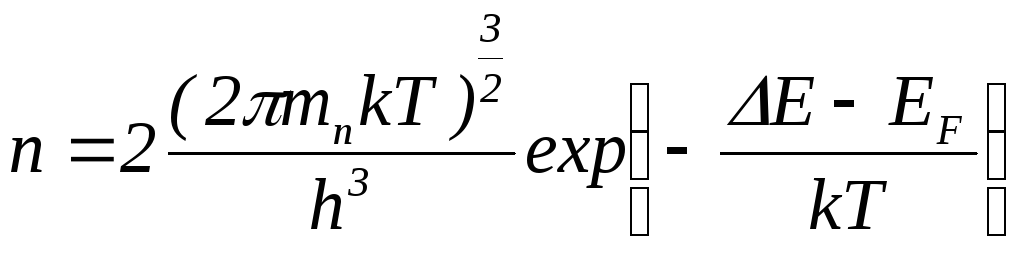 ,
(4.12)
,
(4.12)
Аналогично, для концентрации дырок в валентной зоне можно получить выражение:
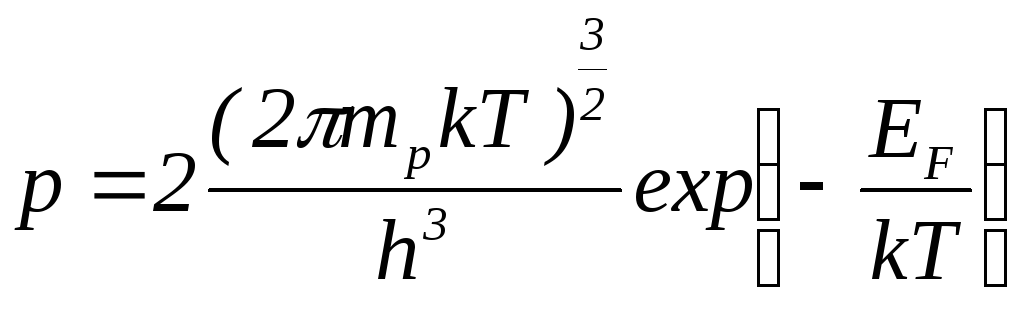 .(4.13)
.(4.13)
В
собственном полупроводнике
концентрации электронов и дырок
одинаковы:
![]() .
Приравнивая правые части выражений
(4.12) и (4.13), получим:
.
Приравнивая правые части выражений
(4.12) и (4.13), получим:
![]() ,
,
![]() ,
,
![]() .
(4.14)
.
(4.14)
Из выражения (4.14) следует, что уровень Ферми в собственном полупроводнике при Т=0 проходит точно посередине запрещённой зоны.
Так как эффективные массы
электронов и дырок не равны (![]() )
то при повышении температурыуровень
Ферми смещается вверх.
)
то при повышении температурыуровень
Ферми смещается вверх.
Подставим формулу (4.14) в выражения для концентрации (4.12) или (4.13), получим:
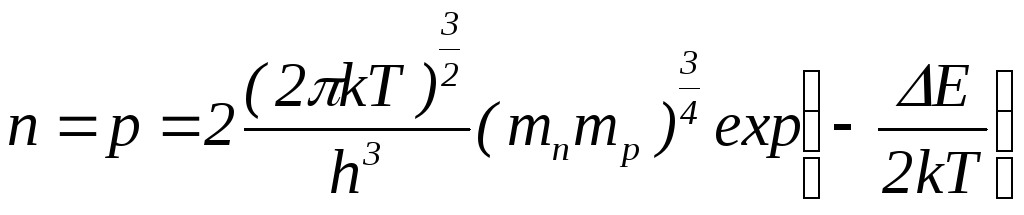 .
(4.15)
.
(4.15)
Пренебрегая слабой
зависимостью от температуры в первом
сомножителе выражения (4.15) (![]() по сравнению с экспоненциальной),
зависимость концентрации носителей в
собственном полупроводнике от температуры
можно представить в простой форме:
по сравнению с экспоненциальной),
зависимость концентрации носителей в
собственном полупроводнике от температуры
можно представить в простой форме:
![]() .
(4.16)
.
(4.16)
Рассмотрим примесный полупроводник. В этом случае расчёт равновесных концентраций и положения уровня Ферми – задача очень сложная, поэтому приведём результаты этих расчётов для двух случаев.
Пусть температура полупроводника сравнительно низкая и примесные атомы ионизированы лишь частично. Тогда концентрация основных носителей заряда определится выражениями:
в электронном полупроводнике:
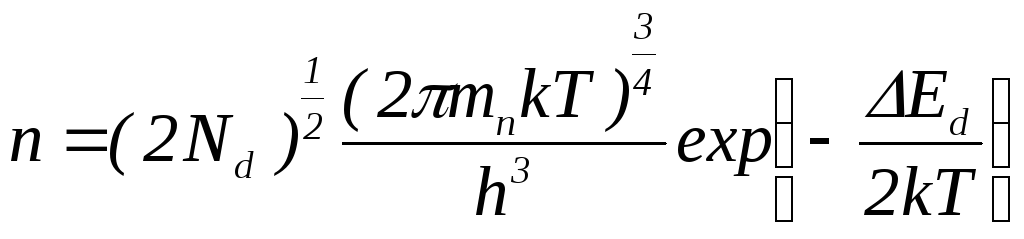 (4.17)
(4.17)
в дырочном полупроводнике:
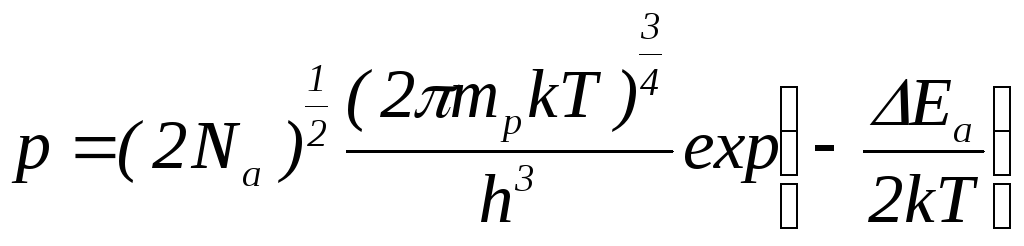 (4.18)
(4.18)
В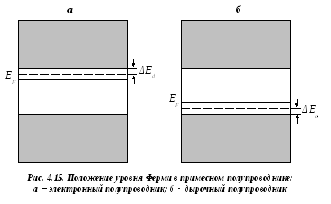 этих выражениях
этих выражениях![]() и
и![]() - концентрации доноров и акцепторов
соответственно;
- концентрации доноров и акцепторов
соответственно;
![]() - расстояние донорного уровня от дна
зоны проводимости,
- расстояние донорного уровня от дна
зоны проводимости,![]() - расстояние акцепторного уровня от
потолка валентной зоны. Величины
- расстояние акцепторного уровня от
потолка валентной зоны. Величины![]() и
и![]() называются энергией активации примесной
проводимости(рис.4.15).
называются энергией активации примесной
проводимости(рис.4.15).
Уровень Ферми в электронном полупроводнике находится в верхней части запрещённой зоны, а в дырочном полупроводнике - в нижней части запрещённой зоны (рис 4.15).
При высоких температурах
атомы примеси ионизированы полностью,
и если собственная проводимость мала,
то можно считать, что
![]() и
и![]() .
.
