
- •«Тюменский государственный нефтегазовый университет»
- •Физика, часть 3
- •Волновая оптика
- •Световой вектор. Уравнение плоской световой волны
- •Интерференция световых волн. Условия, необходимые для осуществления интерференции
- •Условия максимумов и минимумов при интерференции световых волн
- •Интерференция в тонких пленках
- •Кольца Ньютона
- •Контрольные вопросы
- •Дифракция света. Принцип Гюйгенса-Френеля
- •Дифракция от одной щели.
- •Дифракция на одномерной дифракционной решётке
- •Угловая дисперсия и разрешающая способность дифракционной решетки
- •Угловая дисперсия равна:
- •Дифракция рентгеновских лучей на пространственной решетке
- •Поглощение света
- •Поляризация света. Естественный и поляризованный свет
- •1.Явления квантовой оптики
- •1.1. Тепловое излучение и его характеристики. Закон Кирхгофа
- •1.2.Законы излучения абсолютно черного тела. Законы Стефана-Больцмана и Вина
- •1.3.Формула Релея-Джинса. Ультрафиолетовая катастрофа. Квантовая гипотеза и формула Планка
- •1.4.Оптическая пирометрия
- •1.5.Квантовая природа света. Фотон и его характеристики.
- •1.6. Виды фотоэффекта. Внешний фотоэффект и его законы.
- •1.7. Эффект Комптона
- •1.8. Коpпускуляpно-волновой дуализм свойств света
- •1.9. Контрольные вопросы и задачи к разделу «Явления квантовой оптики»
- •2.Элементы квантовой механики
- •2.1. Гипотеза де Бройля. Корпускулярно-волновой дуализм микрочастиц
- •2.2. Соотношение неопределенностей
- •2.3. Волновая функция
- •2.4. Уравнение Шредингера
- •2.5.Задача квантовой механики о движении свободной частицы
- •2.6. Задача квантовой механики о частице в одномерной прямоугольной потенциальной яме
- •1. Пусть размер ямы соизмерим с размерами атома, то есть м. Тогда
- •2. Пусть размер ямы велик, то есть м (свободные электроны в металле). Тогда
- •2.7. Понятие о туннельном эффекте.
- •1.8. Атом водорода в квантовой механике. Квантовые числа
- •Здесь и совпадает с формулой радиуса первой боровской орбиты; численное значение этого параметра равно;a – множитель, который можно определить из условия нормировки волновой функции:
- •2.10. Спин электрона. Принцип Паули
- •2.11. Спектр атома водорода
- •2.12. Распpеделение электpонов в атоме по энеpгетическим состояниям. Пеpиодическая система элементов д.И.Менделеева
- •2.13. Рентгеновское излучение
- •2.14. Поглощение света, спонтанное и вынужденное излучения
- •2.15. Лазеры
- •1. Инверсия населенностей
- •2. 16. Способы создания инверсии населенностей
- •2.17. Положительная обратная связь. Резонатор
- •2.18. Принципиальная схема лазера
- •2.17. Линейный гаpмонический осциллятоp
- •3.6. Понятие о квантовой теории электропроводности металлов
- •3.7. Явление сверхпроводимости. Свойства сверхпроводников
- •Критические температуры перехода для некоторых сверхпроводников
- •4.Зонная теория твёрдых тел
- •4.1. Энергетические зоны электронов в кристалле
- •4.2. Металлы, полупроводники, диэлектрики в зонной теории твёрдых тел
- •4.3.Полупроводники. Собственная проводимость полупроводников
- •4.4. Примесная проводимость полупроводников
- •4.5. Равновесные концентрации носителей заряда в полупроводнике
- •4.6. Зависимость электропроводности полупроводников от температуры
- •Электронно-дырочный переход
- •Внутренний фотоэффект
- •Воздействие излучения на полупроводник. Фоторезистивный эффект
- •Устройство и характеристики фоторезисторов
- •Применение фоторезисторов
- •Фотоэффект в электронно-дырочном переходе. Фото-э.Д.С.
- •Применение вентильного фотоэффекта
- •Биполярный транзистор
- •Характеристики атомного ядра
- •Ядерные силы
- •Понятие об обменном характере ядерных сил. Кванты ядерного поля
- •Радиоактивность
- •Ядерные реакции
- •Деление атомных ядер
- •Элементарные частицы
- •2 Кристаллические решетки твердых тел представляют собой периодические структуры и являются естественными трехмерными дифракционными решетками.
1.7. Эффект Комптона
Корпускулярные свойства света наиболее
отчётливо проявляются в явлении, которое
получило название «эффект Комптона».
Эффект Комптона имеет место при
рассеивании рентгеновского (или γ- излучения) веществом, содержащим лёгкие
атомы. Он заключается в том, что в
рассеянном излучении наряду с излучением
первоначальной длины волны![]() содержится
излучение большей длины волны
содержится
излучение большей длины волны![]() .
.
С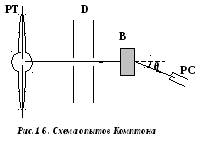 хема
опытов Комптона приведена на рисунке
1.6 . Приведём его описание.
хема
опытов Комптона приведена на рисунке
1.6 . Приведём его описание.
Монохроматическое рентгеновское излучение из рентгеновской трубки (РT) проходит через диафрагмы (D) и узким пучком направляется на рассеивающее вещество (В). Излучение, рассеянное на уголθ,регистрируется рентгеновским спектрографом (РС).
Опыты показали, что разность длин волн рассеянного и падающего излучения связана с углом рассеивания соотношением:
![]() .
(1.39)
.
(1.39)
Постоянная
![]() называется комптоновской длиной волны
электрона; её экспериментальное значение
равно
называется комптоновской длиной волны
электрона; её экспериментальное значение
равно![]() м.
м.
Эффект Комптона нельзя объяснить с позиций классической волновой теории света. В электромагнитной теории рассеивание света рассматривается следующим образом: под влиянием падающей электромагнитной волны в веществе возникают вторичные электромагнитные волны с такой же длиной волны.
Все особенности эффекта Комптона объясняются с квантовой точки зрения: рассеивание рассматривается как процесс упругого столкновения рентгеновского фотона с электронами атомов и молекул.
У лёгких атомов энергия связи внешних
электронов с атомом значительно меньше
энергии рентгеновского фотона (![]() )
и эти электроны можно считать свободными.
)
и эти электроны можно считать свободными.
Р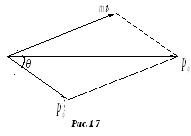 ассмотрим
теорию эффекта Комптона. Пусть на
первоначально покоящийся свободный
электрон падает фотон с энергией
ассмотрим
теорию эффекта Комптона. Пусть на
первоначально покоящийся свободный
электрон падает фотон с энергией![]() и импульсом
и импульсом![]() .
Электрон до столкновения покоится, его
импульс равен нулю, а энергия равна
энергии покоя:
.
Электрон до столкновения покоится, его
импульс равен нулю, а энергия равна
энергии покоя:
![]() .
После столкновения электрон будет
обладать энергией
.
После столкновения электрон будет
обладать энергией
![]() и импульсом
и импульсом
![]() .
Энергия и импульс фотона будут равны
.
Энергия и импульс фотона будут равны![]() и
и![]() .
.
Из законов сохранения энергии и импульса следуют два соотношения:
![]() , (1.40)
, (1.40)
![]() .
(1.41)
.
(1.41)
Рассмотрим взаимную ориентацию векторов
![]() ,
,![]() и
и![]() (рис.1.7 ). Применяя теорему косинусов,
получим связь между модулями этих
векторов:
(рис.1.7 ). Применяя теорему косинусов,
получим связь между модулями этих
векторов:
![]() .
(1.42)
.
(1.42)
Масса электрона отдачи связана с его скоростью соотношением:
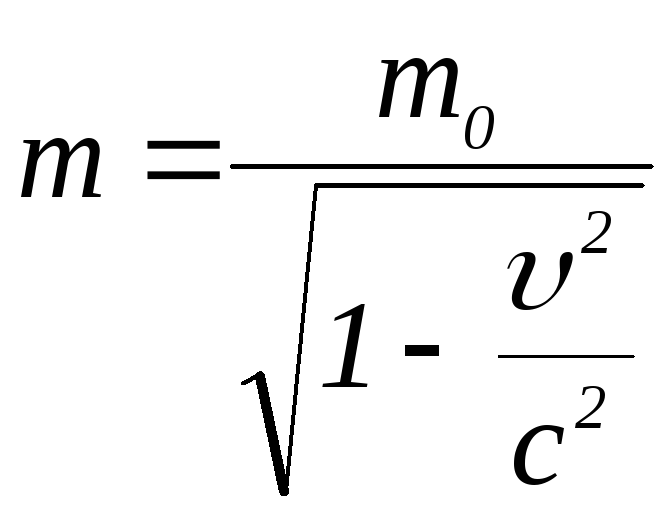 .
(1.43)
.
(1.43)
Объединяя выражения (1.40), (1.42) и (1.43)
получим систему трёх уравнений, содержащую
три неизвестных:
![]() ,
,
![]() и
и
![]() .
Решая эту систему относительно
.
Решая эту систему относительно![]() ,
можно получить:
,
можно получить:
![]() .
(1.44)
.
(1.44)
Разделим обе части уравнения (1.44) на
![]() ,
получим:
,
получим:
![]() (1.45)
(1.45)
Так как
![]() и
и![]() ,
то
,
то
![]() ,
(1.46)
,
(1.46)
или
![]() . (1.47)
. (1.47)
Сравним выражения (1.39) и (1.47). Они совпадают, если
![]() .
(1.48)
.
(1.48)
Подставим значения h,
m0 и
cв формулу (1.46),
получим: ![]() .
Это означает, что теоретическое значение
величины
.
Это означает, что теоретическое значение
величины![]() с большой точностью совпадает с
экспериментальным.
с большой точностью совпадает с
экспериментальным.
Существование в рассеянном излучении
излучения с первоначальной длиной волны
![]() объясняется его рассеиванием на
внутренних, сильно связанных с атомом
электронах. В этом случае электрон
передаёт свою энергию и импульс не
электрону, а атому в целом. Так как масса
атома много больше массы электрона, то
ему передаётся лищь незначительная
часть энергии фотона, и длина волны
рассеянного фотона мало отличается от
длины волны падающего фотона (
объясняется его рассеиванием на
внутренних, сильно связанных с атомом
электронах. В этом случае электрон
передаёт свою энергию и импульс не
электрону, а атому в целом. Так как масса
атома много больше массы электрона, то
ему передаётся лищь незначительная
часть энергии фотона, и длина волны
рассеянного фотона мало отличается от
длины волны падающего фотона (![]() ).
).
