2.1. Періодичні розв’язки диференціальних рівнянь із запізненням

Розглянемо систему диференціальних рівнянь із запізненням вигляду:

, (2.1.1)

з крайовими умовами вигляду

, (2.1.2)

Задача (2.1.1) - (2.1.2) за допомогою замін зводиться до задачі про відшукання періодичного розв’язку з періодом для системи диференціальних рівнянь

, . (2.1.3)

Заміною змінних задача (2.1.3) зводиться до задачі знаходження 2- періодичних розв’язків неавтономної системи вигляду

, (2.1.45)

з додатковою умовою існування періодичного розв’язку

. (2.1.56)

Позначатимемо через розв’язок рівняння (2.1.6) відносно , а через— розв’язок рівняння. Припустимо, що для значеньіз деякого відрізка, виконуються такі умови

1) обмеженості;

2) Ліпшица:

3) власні значення матриці лежать в одиничному крузі;

4) множина точок , що знаходяться в області разом із своїм околом, не порожня.

При виконанні цих припущень періодичний розв’язок системи (2.1.45) будемо шукати як границю рівномірно збіжної послідовності періодичних функцій, що визначаються рекурентними співвідношеннями:

,

,

, (2.1. 67)

, .

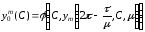Теорема 2.2.1. Якщо система (2.1.45) має періодичний розв’язок , який лежить на поверхні (2.1.56) і виконуються умови 1) - 4), тоді має місце співвідношення

,

визначений рівностями (7).

2.2 Умови існування асимптотичних систем для рівнянь із запізненням

Розглянемо систему диференціальних рівнянь із запізненням:

.

Як відомо, розв'язок задачі Коші для системи (2.2.1) полягає в знаходженні неперервно диференційованої векторної функції, що задовольняє початковим умовам y (t ) = φ(t ) 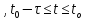і при підстановці обертає систему (2.2.1) в тотожність. Або, потрібно знайти інтегральну криву системи (2.2.1), що починається з деякого відрізка заданої кривої.

Таким чином простір розв'язків системи із запізненням (2.2.1) можна розглядати, як нескінченовимірний простір неперервно диференційованих функцій

Побудуємо систему звичайних диференціальних рівнянь:

до розв'язків якої прямують всі розв'язки вихідної системи із запізненням, тобто яка володіє асимптотичними властивостями щодо системи (2.2.1) [1, c. 739–749].

Слід зазначити, що розв'язок задачі Коші для системи без запізнення (2.2.2) полягає в знаходженні неперервно диференційованої векторної функції z (t ) , що задовольняє початковим умовам , яка при підстановці обертає систему (2.2.2) в тотожність, тобто потрібно знайти інтегральну криву, що починається в заданій точці. І простір розв'язків системи без запізнення (2.2.2) є скінченовимірним.

Означення 2.2.1. Система звичайних диференціальних рівнянь (2.2.2) називається асимптотичною для системи рівнянь із запізненням (2.2.1), якщо довільний розв'язок z (t ) системи (2.2.2) є розв'язком системи (2.2.1) і довільний розв'язок y (t ) системи із запізненням (2.2.1) прямує y (t ) → z(t ) при

t → +∞ до деякого розв'язку системи без запізнення (2.2.2).

Таким чином, система із запізненням (2.2.1) є асимптотичною, якщо в нескінченовимірному просторі Ω існує скінченовимірний многовид, до якого при t → +∞ прямують розв'язки системи (2.2.1) [2, c. 153–167].

Має місце наступна теорема [3, c.].

Теорема 2.2.1. Щоб система із запізненням (2.2.1) мала асимптотичну систему без запізнення (2.2.2), необхідно, щоб існувала векторна функція , при якій всі розв'язки системи звичайних диференціальних рівнянь (2.2.2) задовольняли систему інтегральних рівнянь:

Доведення.

◄Запишемо систему без запізнення (2.2.2) і систему із запізненням (2.2.1) в інтегральному вигляді:

Перепишемо інтегральне рівняння (2.2.4) у вигляді:

і підберемо функцію таким чином, щоб всі розв'язкиz (t ) інтегрального рівняння (2.2.4) були розв'язками інтегрального рівняння (2.2.5). Для цього потрібно, щоб для розв'язків z (t ) рівняння без запізнення (2.2.2) при виконувалася тотожність:

Якщо початкові умови при співпадають, то тотожність (2.2.6) виконується при

де z(s) – розв'язки рівняння без запізнення, визначені при .

Таким чином, всі розв'язки z(t ) системи (2.2.2) є розв'язками системи (2.2.1)►.

Розглянемо систему лінійних диференціальних рівнянь з сталим запізненням

Асимптотичне рівняння шукатимемо також у вигляді системи лінійних диференціальних рівняння першого порядку

з невідомою сталою матрицею Λ . Підставивши в інтегральне рівняння (2.2.3), отримуємо співвідношення

Оскільки розв'язок z (t ) системи без запізнення (2.2.8) має вигляд

,

де – нормована фундаментальна матриця розв'язків, що називається матричним експоненціалом, то підставивши його в інтегральне рівняння (2.2.3), і обчисливши інтеграли, отримаємо

Звідси випливає, що