4. Методичні рекомендації до розв’язання задач

Вправа 1. Дано 2 точки і. Обчислити координати.

Розв’язання. Оскільки і , то

Вправа 2. Обчисліть довжину вектора (із попередньої вправи).

Розв’язання. Оскільки довжина вектора обчислюється за формулою; то

Вправа 3. Чи колінеарні вектори та.

Розв’язання. Оскільки вектор = – вектор вдалося виразити через вектор , то вектори колінеарні.

Вправа 4. Визначити напрямки і довжини колінеарних векторів та.

Розв’язання. Оскільки вектор =, коефіцієнт пропорційності – вектори протилежно напрямлені: ;

довжини: вектор в довший за вектор , а тому – .

Вправа 5. Використовуючи властивості скалярного добутку, обчисліть скалярний добуток векторів та, де.

Розв’язання. =

, оскільки

Вправа 6. Використовуючи властивості векторного добутку, обчисліть векторний добуток векторів та, якщо.

Розв’язання.

.

Наведемо зразки розв’язання задач.

Задача 1. На площині дано 2 вектори ,. Довести, що векториіутворюють базис площини і знайти координати векторау базисі.

Розв’язання. Оскільки координати векторів непропорційні: , то вектори і не колінеарні, а тому утворюють базис площини.

Будь-який вектор однозначно зображається у вигляді лінійної комбінації базисних векторів, а тому і вектор може бути однозначно виражений через вектори та : , або 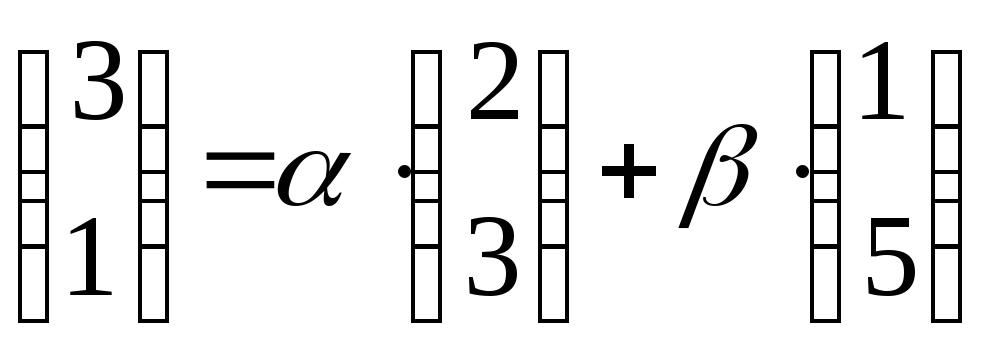; коефіцієнти лінійної комбінації і є координатами вектора у базисі.

Маємо систему двох лінійних рівнянь з двома невідомими: Виразимо з першого рівняння і підставимо в друге рівняння, маємо , звідки аботоді . Отже,

Перевірка: – вірно, співпадає з умовою.

Відповідь: координати вектора у базисі.

Задача 2. Чи колінеарні вектори і, побудовані за векторамиі, якщо

Розв’язання. І спосіб.

Вектори і не колінеарні (оскільки координати векторів непропорційні: ), а тому утворюють базис площини, що визначається векторами і . Оскільки вектори і виражаються через вектори і , то вони лежать у цій площині. Координати векторів іу базисі, відповідно: ,.Так як координати векторів інепропорційні: , то вектори іне колінеарні.

Якщо вектори і – колінеарні (їхні координати пропорційні), то тоді вектори і , відповідно, колінеарні до векторів і , а тому і колінеарні між собою.

ІІ спосіб.

Обчислимо координати векторів іу вихідному базисі (у якому задані координати векторів і ):

, ,

оскільки координати векторів інепропорційні: , то вектори іне колінеарні.

Відповідь: вектори іне колінеарні.

Задача 3. Обчислити кут між векторами і, побудовані за векторамиі, якщоі- одиничні взаємно-ортогональні вектори,

Розв’язання. Вектори утворюють ортонормований базис площини, координати векторів і у цьому базисі: . Із означення скалярного добутку випливає: . Скалярний добуток , модулі векторів тоді ;

Відповідь: кут між векторами

Задача 4. Чи компланарні три вектори ?

Розв’язання. Умовою компланарності трьох векторів є рівність нулю мішаного добутку цих векторів. Відомо, що мішаний добуток трьох векторів в ортонормованому базисі обчислюється як визначник, складений із координат цих векторів:

Оскільки визначник не дорівнює нулю, то вектори не компланарні.

Відповідь: вектори не компланарні.

Задача 5. Знайти довжини ідіагоналей і площу паралелограма, побудованого на векторахі, як на сторонах, якщо, ,

Розв’язання. Площа паралелограма дорівнює модулю векторного добутку векторів, що є сторонами, тобто і : . Обчислимо векторний добуток двох векторів і , використаємо властивості векторного добутку – антикомутативність та властивість сталого множника:

,

=(кв. од.).

Із означення додавання і віднімання векторів маємо наступні векторні рівності (діагоналі паралелограма є (векторними) сумою та різницею (векторів) сторін): ,.

Діагоналі є модулями відповідних векторів та.

;

;

(лін.од.).

;

;

(лін.од.).

Відповідь: площа паралелограма (кв. од.), діагоналі =(лін.од.) і =(лін.од.).

Задача 6. Довести, що вектори ,,утворюють базис і знайти координати векторау цьому базисі, якщо.

Розв’язання. Так як будь-які три некомпланарні вектори утворюють базис простору, то достатньо показати, що вектори ,, – некомпланарні, для цього покажемо, що мішаний добуток не дорівнює нулю:

отже, вектори {,,} утворюють базис простору. Знайдемо координати вектора у цьому базисі: ;

.

Маємо систему трьох лінійних рівнянь з трьома невідомими:

розв’яжемо її за формулами Крамера: де визначники отримані заміною, відповідно, 1-го, 2-го та 3-го стовпців у визначникові стовпцем вільних членів:

,

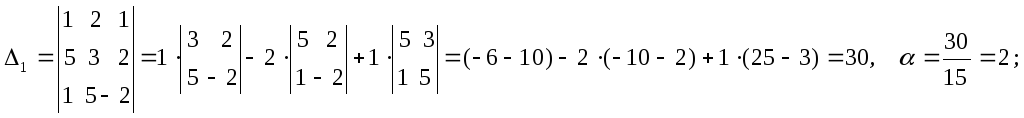
Перевірка: – вірно, співпадає з умовою.

Відповідь: координати вектора у базисі{,,}.

Задача 7. Дано дві суміжні вершини А(-2;5) і В(1;4) паралелограма ABCD і точку O(-4;3) перетину його діагоналей. Знайти:

а) дві його інші вершини;

б) площу S паралелограма;

в) довжини висот паралелограма;

г) внутрішні кути паралелограма;

Скласти рівняння:

д) діагоналей паралелограма;

е) висот паралелограма, проведених із вершини A.

Розв’язання.

Як відомо, діагоналі AC і BD паралелограма точкою перетину діляться навпіл; координати середини відрізка пов’язані з координатами кінців співвідношенням: звідси визначимо координати точокC і D: ,.,, отже координати точкиС(-6;1). О – середина відрізка BD: ,, отже координати точкиD(-9;2).

Внутрішній кут паралелограма – це кут між векторами, що виходять із вершини . Обчислимо ці вектори: ;(від координат кінця вектора віднімаємо координати початку). Тоді .

Скалярний добуток ; довжини векторів (сторін);,

звідки , і кут =. А тоді внутрішній кут =.

Оскільки , то тоді площа паралелограма (кв.од). З іншого боку, , звідки висота, опущена на сторону BA, дорівнює: (лін.од.). Аналогічно, висота, опущена на сторону BC, дорівнює (лін.од.).

Інший спосіб обчислення площі та висот (перевірка). Площа паралелограма дорівнює модулю векторного добутку векторів, що є сторонами, тобто і : = (кв.од).

Склавши рівняння сторін таза двома точками, знайдемо відстань від вершини, що їм не належить (наприклад, вершиниС), до цих сторін, це і є висоти паралелограма. Рівняння прямої за двома точками має вигляд:. Відстань від точкидо прямоївиражається формулою:. Рівняння прямої:, після розкриття пропорції маємо:. Висота, про­ведена з вершиниС, дорівнює (од.).

Рівняння прямої :, або. Висота (од.). Маємо абсолютно ті ж результати.

Рівняння діагоналей та складемо за двома точками: для діагоналі є три точки, вибираємо будь-які дві (та перевіряємо, чи належить третя точка):або.

або .

Рівняння висот, проведених з вершини до сторінта, отримаємо, використавши рівняння прямої за точкою і нормальним вектором:;. Зауважимо, що нор­мальним вектором для висоти, проведеної з вершинидо сторони, є саме векторабо. Рівнянняабо. Нормальним вектором для висоти, проведеної з вершинидо сторониє саме векторабо. Рівняння висоти, проведеної до:або.

Відповідь: вершини ; площа (кв.од); довжини висот (лін.од.), (лін.од.); внутрішні кути =, ; рівняння діагоналей,; рівняння висотта.

Задача 8. Дано трикутник АВС координатами його вершин А(3;10), В(-7;12) і С(-5;4). Скласти рівняння:

а) медіан трикутника АВС;

б) висот трикутника АВС;

в) прямих, що проходять через вершини трикутника АВС паралельно до протилежних сторін.

Розв’язання.

а) Обчислимо координати середин сторін трикутника АВС: нехай – середини, відповідно, сторін. Тоді координати цих точок,,, або,,. Складемо рівняння медіан,,, використаємо рівняння прямої за двома точками:.

Рівняння медіани :, після спрощення маємо:;

рівняння медіани :, або;

рівняння медіани :, або.

б) Рівняння висот отримаємо, скориставшись рівнянням прямої за точкою і нормальним вектором: ;. Зауважимо, що нормальним вектором для висоти, проведеної з вершинидо сторони, є вектор . Рівняння висотиабо.

Нормальним вектором для висоти, проведеної з вершини до сторони, є вектор . Рівнянняабо.

Нормальним вектором для висоти, проведеної з вершини до сторони, є вектор . Рівнянняабо.

в) Для прямих, що проходять через вершини паралельно до протилежних сторін, є точка (вершина) і напрямляючий вектор (протилежної сторони):

||:,. Тоді рівнянняабо.

||:,. Тоді рівнянняабо.

||:,. Тоді рівнянняабо.

Відповідь: рівняння медіан – ,,;

рівняння висот – ,,;

рівняння прямих, що проходять через вершини трикутника паралельно до протилежних сторін, – ,,.

Задача 9. Дано дві вершини А(1;5) і), В(7;4) трикутника АВС і точку Н(-3;0) перетину його висот. Скласти рівняння:

а) сторін трикутника АВС;

б) висот трикутника АВС.

Розв’язання. Для сторони АВ та висот АН і ВН є по дві точки, тому скористаємося рівнянням прямої за двома точками:

рівняння сторони :, або;

рівняння висоти :, або;

рівняння висоти :, або.

Оскільки є висотою трикутника АВС, то і векторє нормальним вектором прямої:,. Тоді рівняння сторониабо.

Аналогічно складаємо рівняння сторони :,||. Тоді рівняння сторониабо.

Рівняння висоти отримаємо з тих же міркувань: ,Тоді рівняння висоти, звідки.

Відповідь: рівняння сторін ,,; рівняння висот,,.

Задача 10. Дано пряму (АВ) і точку Р: А(-5;5), В(4;-1), Р(5;7). Знайти:

а) проекцію О точки на пряму ;

б) точку , симетричну до точки відносно прямої .

Розв’язання.

Складемо рівняння прямої за двома точками:або. Якщо точкаО – проекція точки Р на пряму (АВ), то ||, тоді вектор. Складемо рівняння прямоїза точкоюі нормальним вектором–або. ТочкуО знайдемо як перетин двох прямих , для чого розв’яжемо систему двох рівнянь з двома невідомими:

Точка О має координати .

Щоб знайти точку , симетричну до точкиР відносно прямої (АВ), скористаємося тим, що точка О є серединою відрізка , а томузвідси визначимо координати точки:,,,, отже.

Відповідь: проекція точки Р на пряму ; точка, симетрична до точкиР відносно прямої (АВ), – .

Задача 11. Дано рівняння двох сторін прямокутника: , і точку – його вершину. Обчислити площу прямокутника.

Розв’язання.

Перевіримо, чи можуть сторони прямокутника задаватись відповідно рівняннями та. Для цього перевіримо взаємне положення прямихта: оскільки коефіцієнти при змінних непропорційні, то прямі іперетинаються, отже, вони можуть бути лише сусідніми сторонами прямокутника. Для цього вони мають бути перпендикулярними. Умова перпендикулярності двох прямих:, у нас, отже,.

Перевіримо, чи належить точка даним прямим:та, отже, точка. Тоді відстані від точкидо прямихтаі є довжини сторін прямокутника. Відстань від точки до прямої обчислюється за формулою, тому (од.), (од.). Тоді площа прямокутника (кв.од.).

Відповідь: площа прямокутника (кв.од.).

Задача 12. Дано рівняння двох сторін квадрата: ,. Обчислити його площу.

Розв’язання.

Перевіримо, чи можуть сторони квадрата задаватись відповідно рівняннями та. Для цього перевіримо взаємне положення прямихта: оскільки коефіцієнти при змінних пропорційні, а вільні члени – ні: , то прямі іпаралельні, отже, вони можуть бути лише протилежними сторонами квадрата. Тоді відстань між двома паралельними прямими і є довжиною сторони квадрата. Візьмемо точку на одній з прямих і обчислимо відстань від неї до іншої прямої.

Нехай , покладемо, тоді, координати точки. . Тоді площа квадрата (кв.од.).

Відповідь: площа квадрата (кв.од.).

Задача 13. Скласти рівняння бісектрис кутів, утворених прямими: ,.

Розв’язання.

Перевіримо взаємне розташування прямих :та:: оскільки коефіцієнти при змінних непропорційні, то прямі іперетинаються.

Скористаємося тим фактом, що точки, які лежать на бісектрисах кута, рівновіддалені від сторін кута. Нехай точка лежить на бісектрисі кута, утвореного прямимиі, обчислимо відстані від точки до прямих і: ,, тоді з рівності , маємо тоді , або , звідки маємо сукупність двох рівнянь:

або

Отже, рівняння бісектрис кутів, утворених прямими і, відповідно,:та:.

Зауваження 1. Як відомо, прямі тамають бути взаємно перпендикулярними, тобто має виконуватись умова перпендикулярності двох прямих:, у нас, отже,.

Зауваження 2. Очевидно, що всі прямі і,тамають проходити через одну і ту ж точку, для цього має бути сумісною система 4-ох рівнянь з двома невідомими:Очевидно, що координати точкизадовольняють усі 4 рівняння системи, тобто точкає центром жмутка прямих,,та.

Відповідь: рівняння бісектрис кутів, утворених прямими і, відповідно,:та:.

Задача 14. Дано коло і точку , що не належить колу. Обчислити довжини дотичних, проведених з точки до кола.

Розв’язання.

Перевіримо, чи задача має розв’язок, для цього покажемо, що точка по відношенню до колає зовнішньою точкою. Очевидно, достатньо показати, що відстань від центра коладо точкибільша від радіуса кола. З рівняння кола маємо. Тоді векторйого модуль. Очевидно,і точка– зовнішня по відношенню до кола, а тому існує дві дотичні з точкидо кола, що мають однакові довжини. Нехай– одна з дотичних і точка – точка дотику, тоді– прямокутний, тоді (лін.од.).

Відповідь: довжини дотичних 7 лін.од.

Задача 15. Знайти рівняння кола, що концентричне до даного кола і дотикається до даної прямої .

Розв’язання.

Шукане коло має той же центр , що і дане коло, та радіус, що дорівнює відстані від центра кола до даної прямої. Визначимо центрданого кола. Для цього в рівнянні колавиділимо повні квадрати:, або, звідки. Знайдемо відстань від точкидо прямої:

. А тоді для шуканого кола центр та радіус, відповідно, . І рівняння має виглядабо.

Відповідь: рівняння кола .

Задача 16. У жмутку прямих знайти:

а) пряму, паралельну до осі ;

б) пряму, що проходить через початок координат.

Розв’язання.

Перепишемо рівняння жмутка прямих у вигляді. У рівнянні прямої, паралельної до вісі, коефіцієнт придорівнює нулю:; якщо пряма проходить через початок координат, то вільний член дорівнює нулю:.

а) Коефіцієнт при – це, він має бути рівним нулю:. Дане рівняння має дві змінні, а тому має безліч розв’язків, достатньо вибрати будь-який, відмінний від нульового: наприклад, покладемо, тоді. Підставимо у рівняння, маємо, або, після спрощення маємо.

б) Вільний член дорівнює нулю: . Вибираємо будь-який розв’язок, відмінний від нульового: покладемо, тоді. І тоді рівняння шуканої прямої:або,.

Зауваження: очевидно, центр жмутка – : з рівнянняз рівняння; крім того, координати точкизадовольняють рівняння, перетворюючи кожен з двох доданків у нуль.

Відповідь: ,.

Задача 17. Скласти канонічне рівняння еліпса, рівняння директрис, записати координати фокусів еліпса (які лежать на осі ), якщо відомі відстань між фокусами і ексцентриситет еліпса

Розв’язання.

Канонічне рівняння еліпса ; якщо координати фокусів та . Ексцентриситет , рівняння директрис –. Відстань між фокусами, з умови, отже. Так як за умовою ексцентриситеті, тоді. Маючи, обчислимо. Можемо записати канонічне рівняння еліпса ; координати фокусів, рівняння директрис – .

Відповідь: канонічне рівняння еліпса , рівняння директрис, координати фокусів еліпса.

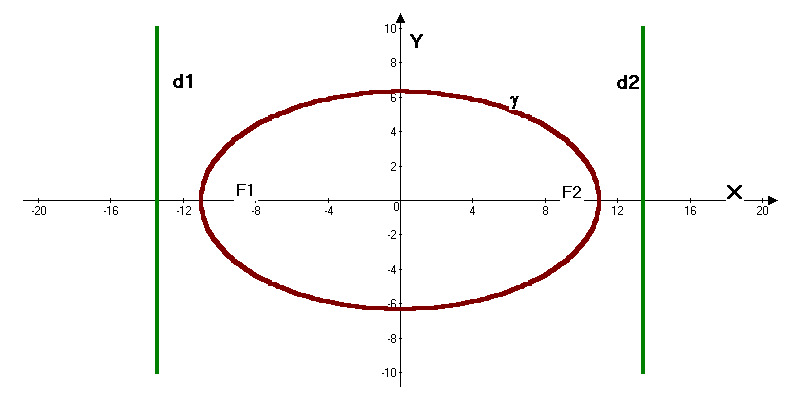
Задача 18. Дано гіперболу своїм рівнянням .Записати рівняння спряженої з нею гіперболи. Знайти координати фокусів, ексцентриситет, рівняння директрис, асимптот даної і спряженої гіпербол.

Розв’язання.

Запишемо канонічне рівняння гіперболи, для цього ліву і праву частини рівняння поділимо на , отримаємо:. Для даної гіперболи дійсною віссю є вісь, отже, фокуси лежать на осіі мають координатиде . У нас , дійсна і уявна півосі гіперболи, відповідно, – , тоді , а тоді координати фокусів для ексцентриситету маємо: . Рівняння директрис –. Рівняння асимптот –.

Канонічне рівняння спряженої гіперболи має вигляд: або. Для даної гіперболи дійсною віссю є вісь, отже, фокуси лежать на осіі мають координатиде . У нас півосі гіперболи: дійсна (на осі ), уявна – тому , а тоді координати фокусів ексцентриситет .

Рівняння директрис – . Рівняння асимптот –виразимо зміннучерез, матимемо те ж рівняння, що і для гіперболиабо.

Відповідь: для даної гіперболи – фокуси, ексцентриситет , директриси, асимптоти;

для спряженої гіперболи – фокуси ексцентриситет , директриси, асимптоти.

Задача 19. Скласти канонічне рівняння параболи, знайти координати фокуса, рівняння директриси, якщо парабола симетрична відносно вісі абсцис і проходить через точку (-2;2).

Розв’язання. Рівняння параболи, що симетрична відносно вісі абсцис, має вигляд , фокуслежить на вісі абсцис і має координати, рівняння директриси. Якщо парабола симетрична відносно вісі ординат, то її рівняння, відповідно,, фокуслежить на вісі ординат і має координати, рівняння директриси.

За умовою, парабола симетрична відносно вісі абсцис, тому її рівняння має вигляд . Відомі координати точки, яка належить параболі (її координати задовольняють рівняння), а тому, підставивши замість зміннихвідповідно-2 та 2, матимемо: , звідки, рівняння параболи. А тоді фокуслежить на вісі абсцис і має координати, рівняння директриси.

Відповідь: канонічне рівняння даної параболи , фокус, рівняння директриси.

Задача 20. Дослідити криву другого порядку (за допомогою перетворення прямокутної системи координат звести рівняння кривої до канонічного виду; записати формули перетворення координат).

Розв’язання. Коефіцієнти рівняння Обчислимо інваріанти перетворень:,. Складаємо характеристичне рівняння,, його коренями є(це є нові значення). Обчислюємо кут поворотусистеми координат:. Маємо(нетабличне значення), тому обчислюємо з формул ,. Тоді,. Матриця перетворення має вигляд:. Відповідно, формули перетворення (повороту системи координат на кут) мають вигляд:.

Запишемо матрицю простіше:та обчислимо нові коефіцієнти при зміннихза формулами:==. Отже,. Записуємо рівняння кривої після повороту на куту вигляді:. З урахуванням наших обчислень, запишемо:, або. Згрупуємо доданки, що містять змінні, та виділимо повні квадрати:;;, виконаємо заміну, звідки– формули перетворення (паралельного перенесення системи координат на вектор). Після цього перетворення рівняння кривої другого порядку набуває вигляду, або– рівняння еліпса в системі координат. Загальні формули перетворення мають вигляд , які після спрощення набувають вигляду:. Координати точки– відносно системи координат.

Таким чином, досліджувана крива другого порядку є еліпс (піввісі якого), побудований в системі координат, де координати точки, а напрями осейвизначають векторита, відповідно.

Відповідь: еліпс , формули перетворення.

Задача 21. Знайти рівняння площини , що проходить через О – початок координат і пряму

Розв’язання. За умовою, точка належить площині. Крім цього, точканалежить прямій, а отже, належить і площині. Векторє напрямляючим вектором прямої, а тому. Таким чином, для шуканої площиниє дві точки і один напрямляючий вектор. Очевидно, і векторСкористаємося рівнянням площини за точкоюі двома напрямляючими векторамита:

маємо . Розкривши визначник за елементами першого рядка , отримаємо або .

Відповідь: рівняння шуканої площини .

Задача 22. Обчислити об’єм тетраедра , площу грані і висоту, опущену з вершини на грань :якщо координати вершин

Розв’язання. Як відомо, об’єм тетраедра (піраміди) дорівнює третині добутку площі основи на висоту, проведену до основи: . З іншого боку, площа трикутника дорівнює половині площі паралелограма:, а площа паралелограма є модуль векторного добутку:, тому. Об’єм паралелепіпеда з сторонамиє модуль мішаного добутку відповідних векторів:.

Обчислимо координати векторів: ,,, векторний добуток:, його модуль:, площу грані:та мішаний добуток:. Тоді об’єм тетраедра:. Висота тетраедра:.

Відповідь: об’єм тетраедра: , площа грані:, висота тетраедра:.

Задача 23. Скласти рівняння площини, якщо точки і симетричні відносно неї. Вказати точку перетину площини з відрізком .

Розв’язання. Із означення симетрії випливає, що середина цього відрізка: належить площині, та відрізокперпендикулярний до шуканої площини. А це означає, що векторє нормальним вектором площини. Складемо рівняння площини за точкою і нормальним вектором:, маємоабо.

Перевірка: вектор має бути колінеарним до нормального вектораплощини: . Середина відрізка – точка– має належати площині:.

Відповідь: рівняння площини , точка перетину відрізказ площиною– точка.

Задача 24. Через точку провести площину, перпендикулярну до двох даних площин: та .

Розв’язання. З умови маємо: нормальні вектори площин та, відповідно,. Оскільки шукана площинаперпендикулярна до площинта, то нормальні вектори цих площин для площиниє напрямляючими векторами. Складемо рівняння площини за точкоюта двома напрямляючими векторами: маємо . Після виконання перетворень, маєм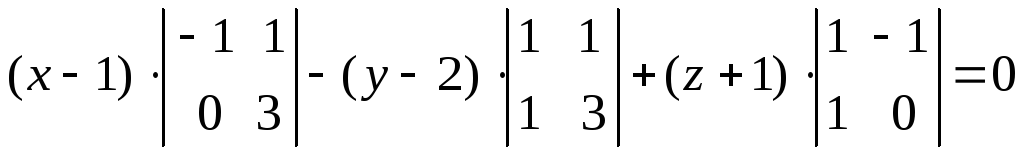о: , або.

Перевірка: координати точки задовольняють рівняння площини:Площинитадо площиниперпендикулярні: умова перпендикулярності площин –, у нас, отже,;, отже,.

Відповідь: рівняння шуканої площини .

Задача 25. Скласти параметричні рівняння прямої , що проходить через дану точку і перетинає дві дані прямі: та . Вказати точки перетину прямої з даними прямими.

Розв’язання. Дослідимо взаємне положення прямих та . З умови маємо: пряма визначається точкою та напрямляючим вектором , пряма – точкою та напрямляючим вектором . Оскільки вектори та неколінеарні (координати не пропорційні), то прямі та або перетинаються, або мимобіжні. Обчислимо мішаний добуток векторів , та . Координати вектора – . Мішаний добуток: , а тому прямі та мимобіжні.

Зауваження: якби прямі та перетиналися, то для розв’язання задачі достатньо було б знайти точку їхнього перетину; шукана пряма з’єднала б тоді цю точку з даною точкою .

Оскільки шукана пряма з прямою та точкою лежить в одній площині , то складемо рівняння цієї площини (за точкою і прямою ). Для площини маємо: , та , а тому . Обчислимо координати вектора , який для площини є другим напрямляючим вектором – : маємоабо , а тоді.

Перевірка: : – вірно, : – вірно, : – вірно. Отже, рівняння складемо вірно.

Аналогічно: так як шукана пряма з прямою та точкою лежить в одній площині , то можемо скласти рівняння цієї площини (за точкою і прямою ). Для площини маємо: , та , а тому . Обчислимо координати вектора , який для площини є другим напрямляючим вектором – : маємо або , а тоді рівняння набуває вигляду або.

Перевірка: : – вірно, : – вірно, : – вірно.

Площина містить прямі та з точкою , площина – прямі з та точкою , а тому шукана пряма є перетином площин та : Складемо параметричні рівняння прямої : точку вже маємо, знайдемо напрямляючий вектор:

.

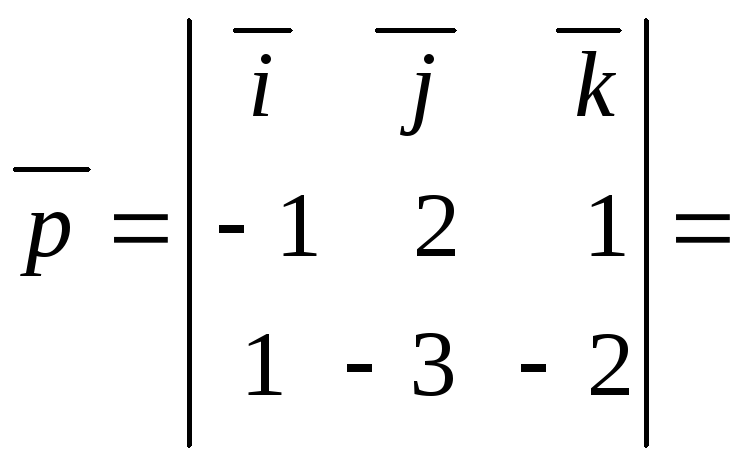
Перевірка: , та– вірно.

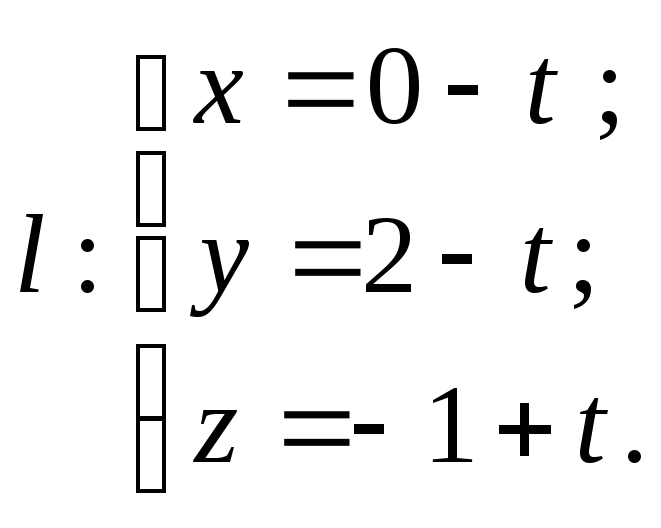Тоді параметричні рівняння прямої набувають вигляду і задача пункту а) розв’язана.

Дослідимо можливість розв’язання задачі пункту б). Прямі та перетинаються, так як вони лежать в одній площині і не паралельні, оскільки їхні напрямляючі вектори та неколінеарні (координати непропорційні). Аналогічно, прямі та перетинаються, бо вони лежать в одній площині і їхні напрямляючі вектори та неколінеарні. А тому знайдемо точки перетину прямої з прямими та .

Спільну точку прямих та можна знайти, розв’язавши систему рівнянь, що містить рівняння та , або ж знайшовши перетин прямої з площиною . Для цього розв’яжемо систему чотирьох рівнянь з чотирма невідомими: Підставивши три останні рівняння у перше, отримаємо:, звідкиабо. Підставимо значення параметрау рівняння прямої , отримаємо координати спільної точки прямих та – Отже,

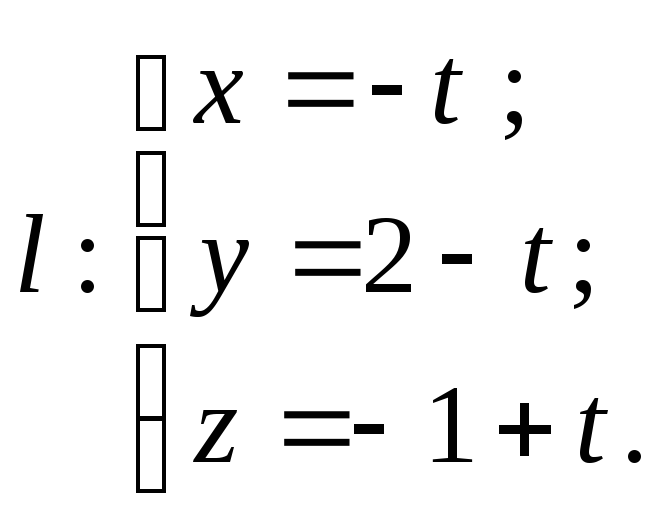Перевірка: точка має належати як прямій, так і прямій : підставимо у рівняння прямої координати точки, маємоабо– точканалежить прямій . Виконаємо другу перевірку: у рівняння підставимо координати точки , маємо . З першого рівняння , з другого –, з третього – теж. Отже, все вірно і точканалежить прямій.

Аналогічно, спільну точку прямих та можна знайти, розв’язавши систему рівнянь, що містить рівняння та , або ж знайшовши перетин прямої з площиною :

Підставивши три останні рівняння у перше, отримаємо: . Підставимо значення параметрау рівняння прямої , отримаємо координати спільної точки прямихта – .

Перевірка: координати точки мають задовольняти рівняння прямих та . Підставимо у рівняння , отримаємо , з кожного рівняння якого маємо: . Отже, точканалежить прямій .

Аналогічно, при підстановці у рівняння маємо: , з кожного рівняння маємо , отже, точканалежить прямій .

Відповідь: рівняння , точки перетину прямої з даними прямими, відповідно, та.

Задача 26. Знайти проекцію точки на площину і точку, симетричну до точки відносно .

Розв’язання. Складемо рівняння прямої , що проходить через дану точкуперпендикулярно даній площині:. Знайдемо точку перетину даної прямої і площини. Для цього розв’яжемо систему чотирьох рівнянь з чотирма невідомими:Підставивши три останні рівняння у перше, отримаємо:, звідкиабо. Підставимо значення параметрау рівняння прямої, отримаємо координати проекції точки на площину–Отже,

Оскільки точка є серединою відрізка, де– точка, симетрична до точкивідносно площини , то координати точок пов’язані співвідношенням:звідси визначимо координати точки:,,, маємо,,. Отже,

Перевірка: вектор має бути колінеарним до нормального вектораплощини: . Середина відрізка – точка– має належати площині:.

Відповідь: проекція точки на площину– точка; точка, симетрична до точкивідносно– точка.

Задача 27. Скласти рівняння проекції прямої на площину .

Розв’язання. Проекція прямоїна площину– це пряма перетину площинита перпендикулярної до неї площини, що проходить через пряму. Оцінимо, що є для рівняння площини: маємо точку, один напрямляючий векторКрім того, нормальний вектор площинидля площинибуде напрямляючим:. Складемо рівняння площиниза точкоюі двома напрямляючими векторами: 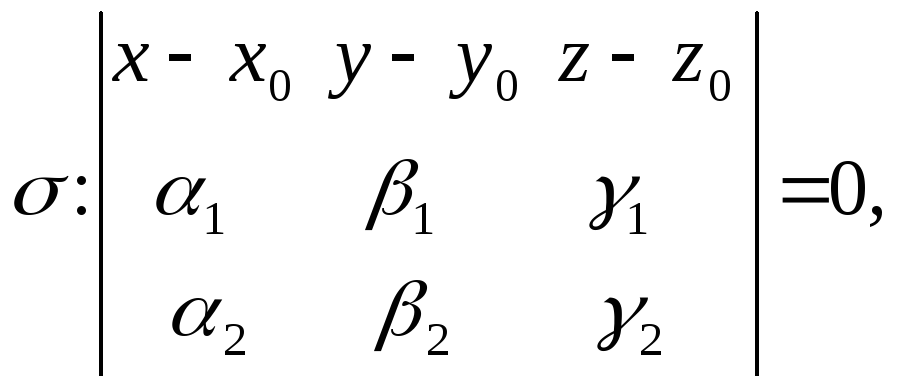маємо . Після виконання перетворень маєм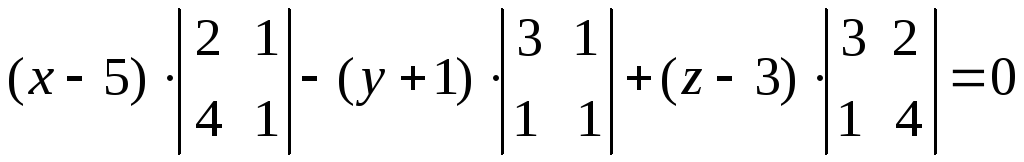о: , або, або. Тоді рівняння проекціїпрямоїна площину–Це і є відповідь (прямазадана як лінія перетину двох площин).

Складемо рівняння проекції прямої у канонічному вигляді. Для цього знайдемо точку, що належить прямій, та її напрямляючий вектор. Для відшукання точки, знайдемо один з розв’язків невизначеної системиПокладемо, наприклад,, тоді отримаємодомножимо перше рівняння на 5 і додамо до другого, матимемо:, звідки, а тоді з першого рівняння, звідки точка –.

Координати напрямляючого вектора прямої обчислимо із співвідношення: ,.

Відповідь: рівняння проекції прямоїабо.

Задача 28. Скласти рівняння геометричного місця точок, рівновіддалених від двох даних площин та .

Розв’язання. Нехай точка належить шуканому геометричному місцю точок. Тоді вона знаходиться на однакових відстанях від обох площин. Запишемо відстані від точкидо однієї і другої площин і прирівняємо їх. Скористаємося формулою відстані від точки до площини:; маємо відстані до площин,а тоді, звідки. Розв’язуючи дане рівняння, приходимо до сукупності двох рівнянь, які і дають нам шукане геометричне місце точок:абоа тодіВідповіддю є об’єднання двох взаємно перпендикулярних площинта.

Перевірка (перпендикулярності площин та):, отже. Іншою перевіркою правильності обчислень може слугувати той факт, що всі чотири площини (і дані, і шукані) проходять через одну і ту ж пряму.

Відповідь: від даних двох площин та рівновіддаленими є площинита.

Задача 29. На відстані 5 одиниць від даної площини провести площину, паралельну їй.

Розв’язання. Нехай точка належить шуканій площині. Тоді вона знаходиться на відстані 5 одиниць від площини. Маємо:, а тодіабо, звідки. Шукане геометричне місце точок є сукупність двох паралельних площин:що паралельні до даної площини.

Відповідь: рівняння шуканих площин .

Задача 30. Знайти точку перетину прямої і площини .

Розв’язання. Перепишемо рівняння прямої у параметричному вигляді, врахуємо, що точка прямої , напрямляючий вектор:Для знаходження спільної точки площини і прямої, розв’яжемо систему рівнянь –Підставимо три останні рівняння у перше, матимемо:, звідкиабо. Повертаючись до трьох останніх рівнянь системи, маємо:Отже, спільна точка має координати:

Виконаємо перевірку, для чого підставимо координати точки у рівняння прямої та площини:

, маємо – все вірно, отже,;

Відповідь: точка перетину прямої і площини

Задача 31. Встановити взаємне розташування двох прямих і

Розв’язання.

Поставимо кожній прямій у відповідність одну точку і напрямляючий вектор – .

Знайдемо точку, що належить прямій , та її напрямляючий вектор. Для відшукання точки, знайдемо один з розв’язків невизначеної системиПокладемо, наприклад,, тоді отримаємоабододамо перше рівняння до другого, матимемо:, звідки, а тоді з другого рівняння, або звідки точка – . Перевірка: координати точкиобчислені правильно, якщо вони задовольняють кожне рівняння системи:– вірно.

Координати напрямляючого вектора прямої обчислимо із співвідношення: ;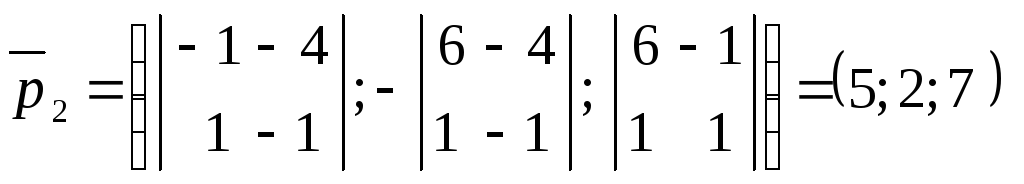. Перевірка: вектормає бути паралельним і до площини, і до:– отже, все вірно.

Отже, для прямої .

Напрямляючі вектори тапрямих неколінеарні, бо їхні координати непропорційні:, тому прямі або мимобіжні, або перетинаються. Щоб визначитися із взаємним розташуванням цих прямих, обчислимо мішаний добуток векторів, якщо він дорівнює нулю, то прямі і перетинаються, якщо не дорівнює нулю – мимобіжні (координати вектора):

, після обчислень маємо , отже, прямі і перетинаються.

Зауваження: якби вектори прямих виявилися колінеарними (тобто їхні координати пропорційні), то тоді треба перевіряти, чи колінеарні векторита. Якщо так, то прямі і співпадають, ні – прямі і паралельні.

Відповідь: прямі і перетинаються.

Задача 32. Дослідити тип поверхні другого порядку: . Вказати систему координат, в якій поверхня має канонічний вигляд.

Розв’язання. Перепишемо рівняння поверхні, згрупувавши окремо доданки, що містять змінні :

або . Доповнимо вирази в дужках до повних квадратів:

,

, зводимо подібні, отримаємо: , або. Поділимо на:, виконаємо заміну змінних:та виразимо старі змінні через нові, звідки. Після заміни змінних, маємо– канонічне рівняння еліптичного параболоїда в системі координат, отриманій із початкової системи координат паралельним перенесенням в точку.

Відповідь: дана поверхня є еліптичний параболоїд; у системі координат , де,, рівняння поверхні – .