2.2. З а д а ч і

Задача №7. Дано дві суміжні вершини A і B паралелограма ABCD і точку O перетину його діагоналей. Знайти:

а) дві його інші вершини;

б) площу паралелограма;

в) довжини висот паралелограма;

г) внутрішні кути іпаралелограма;

Скласти рівняння:

д) діагоналей паралелограма;

е) висот паралелограма, проведених з вершини A.

1. 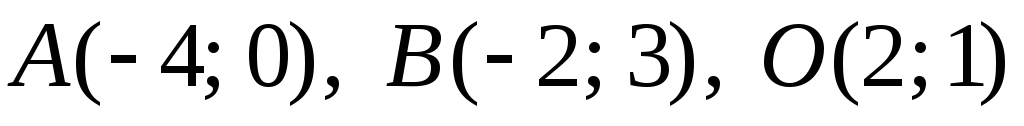;	16. ;
2. ;	17. ;
3. ;	18. ;
4. ;	19. ;
5. ;	20. ;
6. ;	21. ;
7. 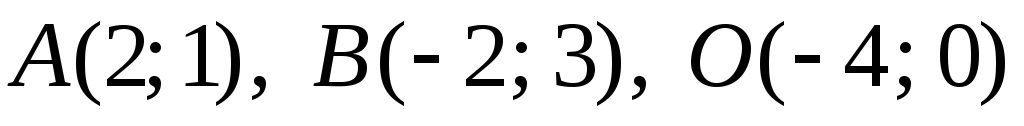;	22. ;
8. ;	23. ;
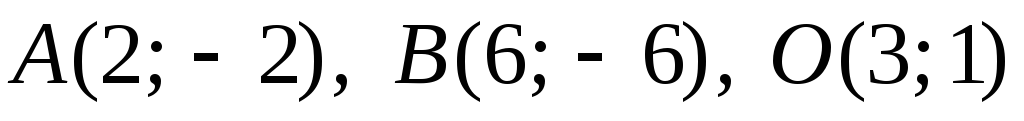9. ;	24. ;
10. 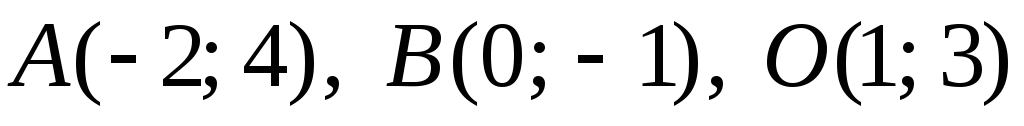;	25. ;
11. ;	26. ;
12. ;	27. ;
13. ;	28. ;
14. ;	29. ;
15. ;	30..

Задача №8. Дано координатами його вершин. Скласти рівняння:

а) медіан ;

б) висот ;

в) прямих, що проходять через вершини паралельно до протилежних сторін.

1. ;	16. ;
2. ;	17. ;
3. ;	18. ;
4. 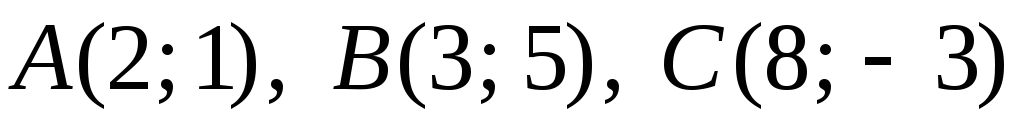;	19. ;
5. ;	20. ;
6. ;	21. ;
7. ;	22. ;
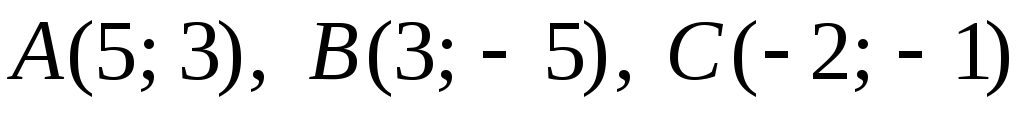8. ;	23. ;
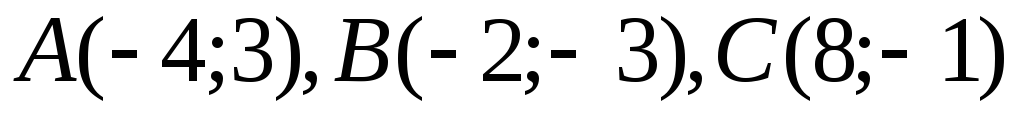9. ;	24. ;
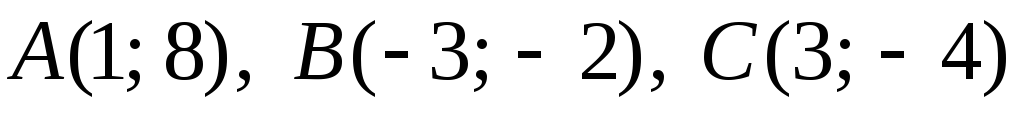10. ;	25. ;
11. ;	26. ;
12. ;	27. ;
13. ;	28. ;
14. ;	29. ;
15. ;	30. .

Задача №9. Дано 2 вершини A і B і точкуH – перетину його висот. Скласти рівняння:

а) сторін ;

б) висот .

1. ;	16. ;
2. ;	17. ;
3. ;	18. ;
4. ;	19. ;
5. 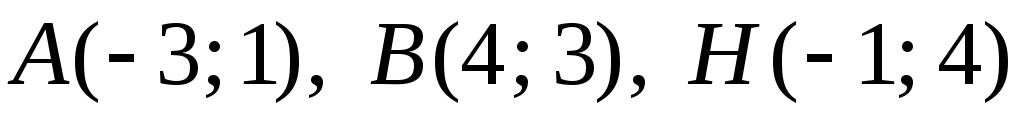;	20. ;
6. 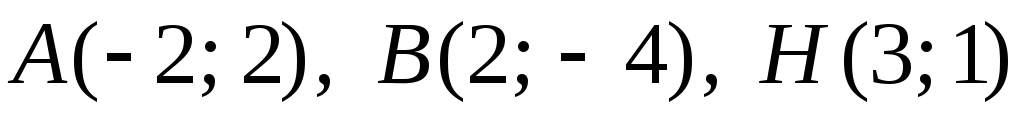;	21. ;
7. ;	22. ;
8. ;	23. ;
9. ;	24. ;
10. ;	25. ;
11. ;	26. ;
12. ;	27. ;
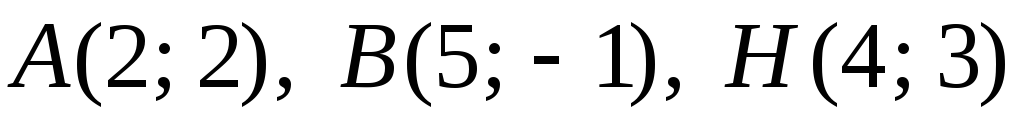13. ;	28. ;
14. ;	29. ;
15. ;	30. .

Задача №10. Дано пряму AB і точку P. Знайти:

а) проекцію точки P на пряму AB;

б) точку, симетричну до точки P відносно AB:

1. ;	16. ;
2. ;	17. ;
3. ;	18. ;
4. ;	19. ;
5. ;	20. ;
6. ;	21. ;
7. ;	22. ;
8. ;	23. ;
9. ;	24. ;
10. ;	25. ;
11. ;	26. ;
12. ;	27. ;
13. ;	28. ;
14. 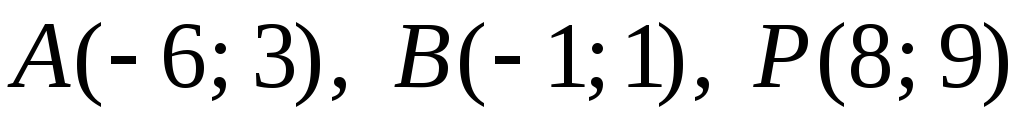;	29. ;
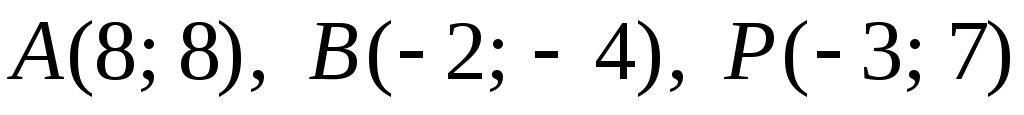15. ;	30. .

Задача №11. Дано рівняння двох сторін прямокутника і точку A – його вершину. Обчислити площу прямокутника.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. 

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

26. ;

27. ;

28. 

29. ;

30. .

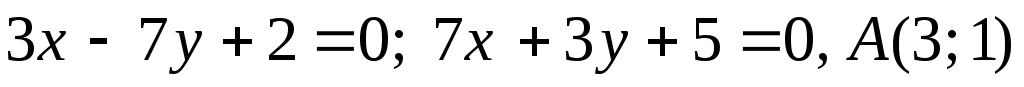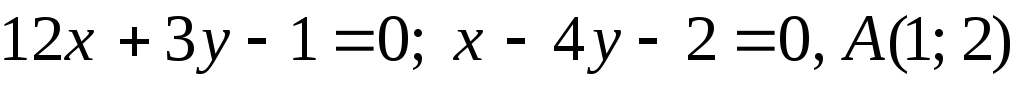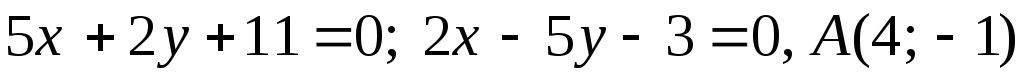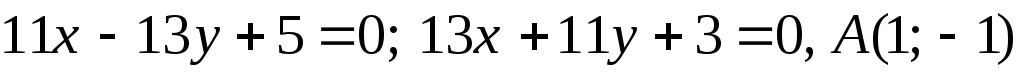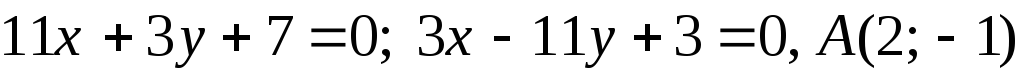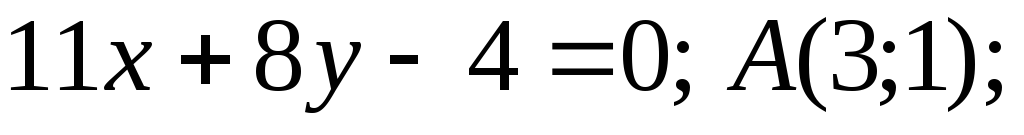
Задача №12. Дано рівняння двох сторін квадрата. Обчислити його площу:

1. ;	16. ;
2. ;	17. ;
3. ;	18. ;
4. ;	19. ;
5. ;	20. ;
6. ;	21.;
7. ;	22. ;
8. ;	23.
9. ;	24. ;
10.;	25. ;
11. ;	26. ;
12. ;	27. ;
13. ;	28. ;
14. ;	29. ;
15. ;	30..

Задача №13. Скласти рівняння бісектрис кутів, утворених прямими:

1. ;	16. ;
2. ;	17. ;
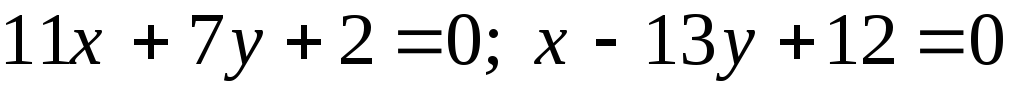3. ;	18. ;
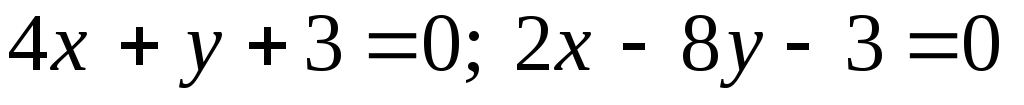4. ;	19. ;
5. ;	20. ;
6. ;	21. ;
7. ;	22. ;
8. ;	23. ;
9. ;	24. ;
10. ;	25. ;
11. ;	26. ;
12. ;	27. ;
13. ;	28. ;
14. ;	29. ;
15. 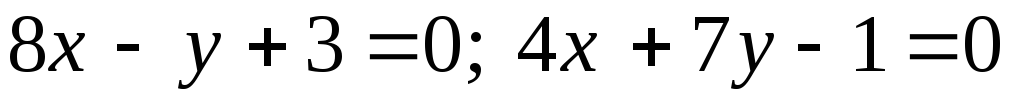;	30. .

Задача №14. Дано коло і точкуP, що не належить колу. Обчислити довжини дотичних, проведених з точки P до кола :

1. ;	16. ;
2. ;	17. ;
3. ;	18. ;
4. ;	19. ;
5. ;	20. ;
6. ;	21. ;
;	22. ;
8. ;	23. ;
9. ;	24. ;
10. ;	25. ;
;	26 ;
12. ;	27. ;
13. ;	28. ;
14. ;	29. ;
15. ;	30. .

Задача №15. Знайти рівняння кола, що концентричне до даного кола і дотикається до даної прямої:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

26. ;

27. ;

28. ;

29. ;

30. .

Задача №16. У жмутку прямих знайти:

а) пряму, паралельну до осі ;

б) пряму, що проходить через початок координат.

1. ;	16 ;
2. ;	17. ;
3. ;	18. ;
4. ;	19. ;
5. ;	20. ;
6. ;	21. ;
7. ;	22. ;
8. ;	23. ;
9. ;	24. ;
10. ;	25. ;
11. ;	26. ;
12. ;	27. ;
13. ;	28. ;
14. ;	29. ;
15. ;	30. .

Задача №17. Скласти канонічне рівняння еліпса, рівняння директрис, записати координати фокусів еліпса (які лежать на осі ), якщо відомі відстань між фокусами і ексцентриситет еліпса. Зобразити все на малюнку.

1. ;	11. ;	21. ;
2. ;	12. ;	22. ;
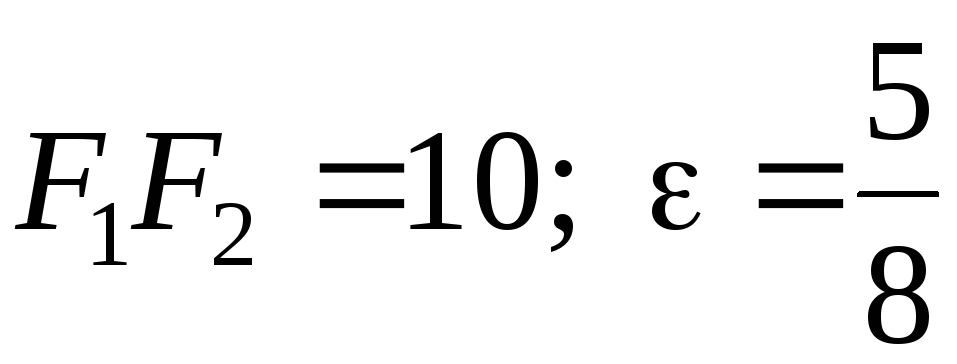3. ;	13. ;	23. ;
4. ;	14. ;	24. ;
5. ;	15. ;	25. ;
6. ;	16. ;	26. ;
7. ;	17. ;	27. ;
8. ;	18. 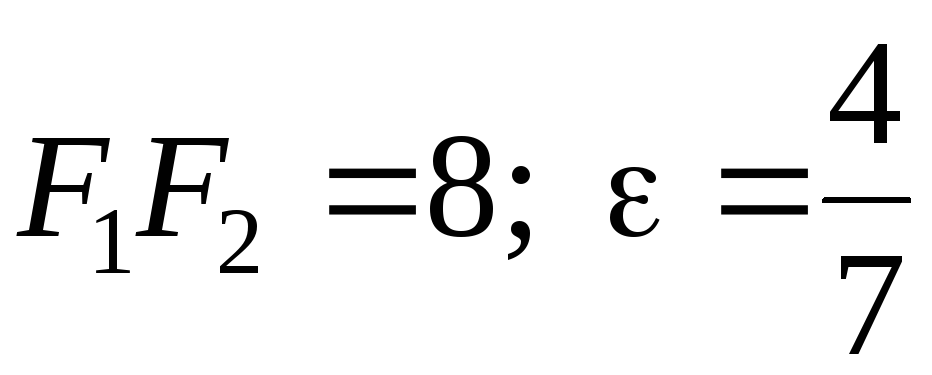;	28. ;
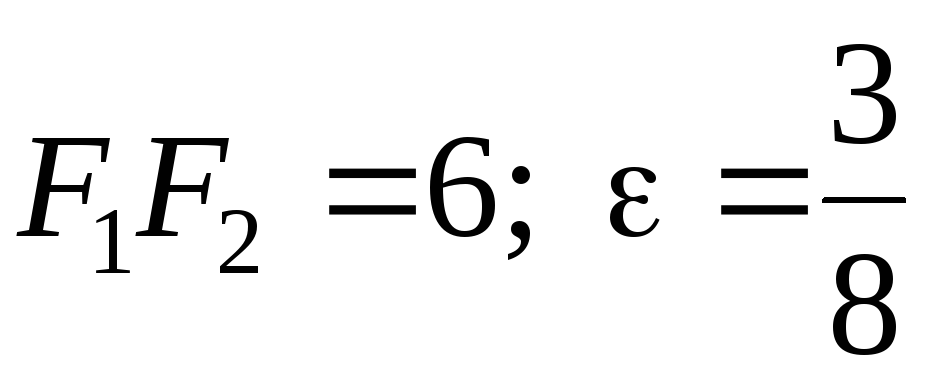9. ;	19. ;	29. ;
10. 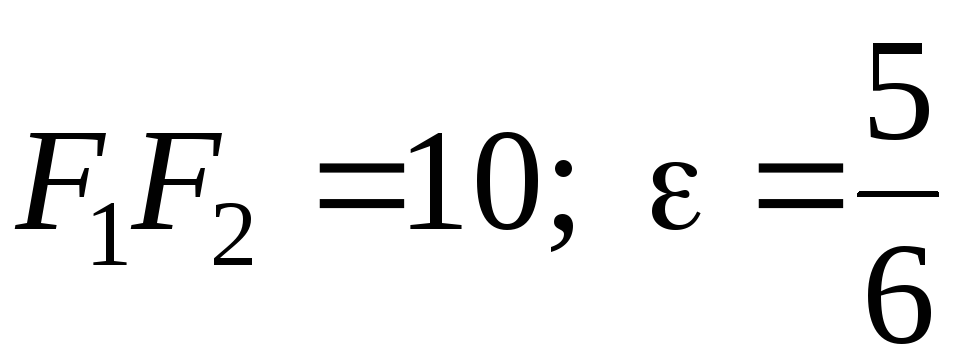;	20. ;	30. .

Задача №18. Дано гіперболу своїм рівнянням. Записати рівняння спряженої з нею гіперболи. Знайти фокуси, ексцентриситет, директриси і асимптоти даної і спряженої гіпербол. Зобразити все на малюнку:

1. ;	11. ;	21. ;
2.;	12. ;	22. ;
3.;	13. ;	23. ;
4.;	14. ;	24. ;
5.;	15. ;	25. ;
6.;	16. ;	26. ;
7.;	17. ;	27. ;
8.;	18. ;	28. ;
9.;	19. ;	29. ;
10.;	20. ;	30. .

Задача №19. Скласти канонічне рівняння параболи, записати координати фокуса, рівняння директриси, зобразити все на малюнку, якщо:

1) відстань від фокуса, що лежить на осі , до вершини дорівнює 5;

2) відстань від фокуса, що лежить на осі , до директриси дорівнює 6;

3) відстань від вершини до директриси, що паралельна на осі , дорівнює 4;

4) фокус має координати ;

5) рівняння директриси ;

6) відстань від фокуса, що лежить на осі , до вершини дорівнює 3;

7) відстань від фокуса, що лежить на осі , до директриси дорівнює 2;

8) відстань від фокуса, що лежить на осі , до директриси дорівнює 5;

9) відстань від вершини до директриси, що паралельна осі дорівнює 7;

10) парабола симетрична відносно вісі і проходить через точку;

11) парабола симетрична відносно вісі і проходить через точку;

12) парабола симетрична відносно вісі і проходить через точку;

13) парабола симетрична відносно вісі і проходить через точку;

14) парабола симетрична відносно вісі і проходить через точку;

15) парабола симетрична відносно вісі і проходить через точку;

16) директриса має рівняння ;

17) директриса має рівняння ;

18) директриса має рівняння ;

19) фокус має координати ;

20) фокус має координати ;

21) парабола симетрична відносно вісі і проходить через точку;

22) парабола симетрична відносно вісі і проходить через точку;

23) парабола симетрична відносно вісі і проходить через точку;

24) парабола симетрична відносно вісі і проходить через точку;

25) парабола симетрична відносно вісі і проходить через точку;

26) фокус має координати ;

27) фокус має координати ;

28) директриса має рівняння ;

29) директриса має рівняння ;

30) директриса має рівняння .

Задача №20. Дослідити криву другого порядку (за допомогою перетворення прямокутної системи координат звести рівняння кривої до канонічного виду; записати формули перетворення координат, зобразити на малюнку).

1. ;	16. ;
2. ;	17. ;
3. ;	18.;
4. ;	19. ;
5. ;	20. ;
6. ;	21. ;
7. ;	22. ;
8. ;	23. ;
9. ;	24.;
10. ;	25. ;
11. ;	26. ;
12. ;	27. ;
13. ;	28. ;
14. ;	29. ;
15. ;	30..