1 Основные понятия теории множеств. Множества и операции над ними.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.
Например, перечислением заданы следующие множества:
А={1,2,3,5,7} — множество чисел
Х={x1,x2,...,xn} — множество некоторых элементов x1,x2,...,xn
N={1,2,...,n} — множество натуральных чисел
Z={0,±1,±2,...,±n} — множество целых чисел
Множество (-∞;+∞) называется числовой прямой, а любое число — точкой этой прямой. Пусть a — произвольная точка числовой прямой иδ — положительное число. Интервал (a-δ; a+δ) называется δ-окрестностью точки а.
Множество Х ограничено сверху (снизу), если существует такое число c, что для любого x ∈ X выполняется неравенство x≤с (x≥c). Число с в этом случае называется верхней(нижней) гранью множества Х. Множество, ограниченное и сверху и снизу, называется ограниченным. Наименьшая (наибольшая) из верхних (нижних) граней множества называется точной верхней (нижней) гранью этого множества.
Основные числовые множества
|
N |
{1,2,3,...,n} Множество всех натуральных чисел |
|
Z |
{0, ±1, ±2, ±3,...} Множество целых чисел. Множество целых чисел включает в себя множество натуральных. |
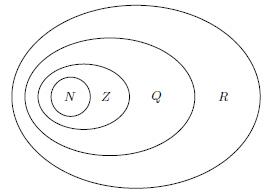
Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается Ø.
Элементы логической символики
|
→ |
"следует", "выполняется" |
|
↔ |
равносильность утверждения |
|
: |
"такой, что" |
Запись ∀x: |x|<2 → x2 < 4 означает: для каждого x такого, что |x|<2, выполняется неравенство x2 < 4.
Квантор
При записи математических выражений часто используются кванторы.
Квантором называется логический символ, который характеризует следующие за ним элементы в количественном отношении.
∀- квантор общности, используется вместо слов "для всех", "для любого".
∃- квантор существования, используется вместо слов "существует", "имеется". Используется также сочетание символов ∃!, которое читается как существует единственный.
Операции над множествами
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Свойства операций над множествами
Свойства перестановочности
A ∪ B = B ∪ A A ∩ B = B ∩ A
Сочетательное свойство
(A ∪ B) ∪ C = A ∪ (B ∪ C) (A ∩ B) ∩ C = A ∩ (B ∩ C)
2 Понятие множества. Способы задания множеств.
Множества.
Множество - совокупность различных элементов, мыслимая как единое целое Элемент множества - объект А называется элементом множества, если он обладает характеристическим свойствами этого множества. Способы задания множеств. 1) Перечислением - и перечислении множества его элементы принято заключать в фигурные скобки: {2,4,6,...} — множество четных чисел, {3,6,9,...}— множество чисел кратных трем. Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем. 2) Описание свойств - для задания (описания) некоторого множества X, состоящего из элементов, обладающих свойством α, используют запись X={x |α(x)}. Читается как: «X — множество элементов x таких, что α(x)". Например, Y={y | y∈N и y<7} — множество натуральных чисел, меньших 7.
3 Виды множеств. Булеан множеств. Универсум.
Пустое множество-множество, не содержащее ни одного элемента.
Пустое множество является частью любого множества.
Пример:
Множество
всех действительных корней уравнения 
пусто.
Множество считается определенным , если указаны все его элементы.Эти элементы могут быть указаны с помощью некоторого общего признака или с помощью некоторого списка, где обозначены все элементы.Последний способ возможен только в том случае, если множество имеет конечное число элементов.
Конечное множество-множество, состоящее из конечного числа элементов.
Пример:
Множество всех студентов факультета математики и информатики.
Основной характеристикой конечного множества является число его элементов.
Бесконечное множество-непустое множество, не являющееся конечным.
Пример:
Множество натуральных чисел является бесконечным.
Упорядоченное множество
Множество, каждому элементу которого поставлено в соответствие некоторое число (немер этого элемента) от 1 до n, где n - число элементов множества, так что различным элементам соответствуют различные числа.
Каждое конечное множество можно сделать упорядоченным, если, например, переписать все элементы в некоторый список (a, b, c, d,...), а затемпоставить в соответствие каждому элементу номер места, нк котором он стоит в списке.
Множество всех подмножеств множества Р называется булеаном множества Р и обозначается В(Р). Булеан множества Р={а,в,с}, имеет вид
В(Р)={, {с}, {b}, {b,с},{a},{a,с},{a,b},{a,b,с}}.
Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна) в виде замкнутых кривых, ограничивающих области, которым ставятся в соответствие элементы тех или иных множеств. На рис.1 показано два множества:
Р={1,2,3,4,5,6} и К={1,2,3}. По диаграмме видно, что К Р.
Множества не имеют общих элементов – изображаются непересекающимися кругами.
С
K
Р В
Рис. 1
Универсальное множество (иногда используется термин «полное множество») обозначается символом I. Множество I – это множество всех тех элементов, которые участвуют в данном рассуждении.
Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.
На рис. 2 показан пример универсального множества
I = {0,1,2,3,4,5,6,7,8,9} и двух его подмножеств Р = {2} и Q = {2,3,5,7}, где
Р- множество четных простых чисел, а Q – множество всех простых чисел, меньше 10
Рис. 2
5 Операции над множествами. Диаграммы Эйлера.
Операции над множествами
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Свойства операций над множествами
Свойства перестановочности
A ∪ B = B ∪ A A ∩ B = B ∩ A
Сочетательное свойство
(A ∪ B) ∪ C = A ∪ (B ∪ C) (A ∩ B) ∩ C = A ∩ (B ∩ C)
Венн Джон (1834—1923) — английский логик, профессор, член Королевского общества [24, с. 82].
Чтобы повысить наглядность представления множеств и отношений между ними, используют диаграммы
Венна (иногда их называют диаграммами Эйлера [14], кругами Эйлера [16], диаграммами Эйлера-Венна [46]) в виде замкнутых кривых, ограничивающих области, которым ставятся в соответствие элементы тех или иных множеств. На рис. 1 показаны два множества:
P = {1, 2, 3, 4, 5, 6};
K = {1, 2, 3}.
Непосредственно из диаграммы видно, что K ⊂ P. Если требуется показать, что множества не имеют общих элементов, эти множества изображают непересекающимися кругами. На рис. 2 непересекающимися являются множества B = {a, b}; C = {e, f}.
Одним из важнейших понятий теории множеств является понятие универсального множества (иногда используется термин «полное множество» [24, с. 454], а также «универсум» [14, с. 7]). Обозначается оно обычно символом I (либо U). Множество I — это множество
всех тех элементов, которые участвуют в данном рассуждении. Любое рассматриваемое при этом множество является подмножеством универсального множества. Например, если рассматриваются различные множества целых положительных чисел за исключением
нуля, то универсальным можно считать множество всех натуральных чисел. 14 На диаграммах Венна универсальные множества изображаются в виде прямоугольников, внутри которых размещаются круги, обозначающие подмножества соответствующих универсальных множеств. На рис. 3 показан пример универсального множества I = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
и двух его подмножеств P = {2} и Q = {2, 3, 5, 7), где P —множество четных простых чисел, а Q — множество всех
простых чисел, меньших 10.В общем случае универсальным может быть любое непустое множество.
6 Отношения. Унарные, бинарные, тернарные отношения.
Понятие бинарного отношения
Пусть
дано декартово произведение двух
непустых множеств А и В, при этом множества
могут быть любыми: непересекающимися,
равными, входящими одно в другое и т.д.
Элементами множества АхВ являются
упорядоченные пары
,
где
i = 1,2, … ,|A|; j= 1,2,…,|B|. Всякое подмножество
декартова произведения АхВ называется
бинарным отношением, определенным на
паре множеств А и В. Для обозначения
бинарного отношения принимают знак R.
Поскольку R – это подмножество множества
AxB, то можно записать
.
Если же требуется указать, что (а, b)
,
т.е. между элементами а
и
b
,существует
отношение R, то пишут aRb. Пусть напрмер:
А={1,2,3}; B={1,2,3,4,5,6} (24)
Множество
АхВ содержит 18 упорядоченных пар. Выделим
на этом множестве отношение «больше»:
a>b, где а
и
b
,
тогда
R = {(2,1),(3,1),(3,2)},
Многие
авторы понятие бинарного отношения
определяют через квадрат множества.
Например, В.А. Горбатов пишет: «Бинарным
отношением Т в множестве М называется
подмножество его квадрата:
»
Задавать бинарные отношения можно различными способами. Наиболее употребительным является табличный способ. Его основу составляет прямоугольная система координат, где по одной оси откладываются элементы одного множества, по второй – другого. Пересечение координат образуют точки, обозначающие элементы декартового произведения. Бинарные отношения задаются двухмерными системами координат. Очевидно, что все элементы декартова произведения трех множеств могут быть представлены в трехмерной системе координат, четырёх множеств – в четырехмерной системе и т.д.
Второй способ представления отношений – в виде графов – применяется так же часто, как и первый (табличный). Способ задания отношений с помощью сечений используется реже.
Симметрия отношений
Пусть
между элементами а
и
b
имеется отношение R. Переставим местами
a и b. Если при этом отношение R сохранится,
то такое отношение симметричное.
Отношение является асимметричным, если оно имеет место между элементами a и b, но не отсутствует между элементами b и а.
Отношение является несимметричным в том случае, если оно не является симметричным, т.е. если имеет место отношение aRb, то отношение bRa может быть, но может и не быть.
Кроме симметричных, асимметричных, несимметричных отношений в математической литературе рассматриваются еще один вид симметрии – антисимметричность. Если отношения aRb и bRa имеют место лишь при a=b, то отношение R называют антисимметричным.
Транзитивность отношений
Любое отношение R в множестве М является либо транзитивным, либо интранзитивным ,либо не транзитивным.
Отношение R в множестве М называется транзитивным, если из aRb и bRc следует aRc.
Отношение называется интранзитивным, если из аRb и bRc следует, что утверждение aRc является ложным.
Отношение называется нетранзитивным, если оно не является транзитивным и не является интранзитивным, т.е. из того что имеет место отношение aRb и bRc, утверждение aRc может быть и истинным, и ложным.
Рефлексивность отношений
Отношение
R в множестве М называется рефлексивным,
если ни один элемент а
утверждение aRa является истинным.
Отношения
называются антирефлексивными, если ни
один элемент а
не находится в отношении R с самим собой,
такие отношения называются иррефлексивными).
Существуют отношения не являющиеся не рефлексивными, ни антирефлексивными. Пусть, например, М – множество точек на плоскости. Рассмотрим отношение: «точка а симметрична точке b относительно прямой, лежащей в той же плоскости». Если точки лежат не на прямой, то утверждения аRа и bRb являются ложными. Но все точки, лежащие на прямой, симметричны сами по себе. Следовательно, данное отношение не является рефлексивным и не является антирефлексивным.
Отношения эквивалентности
Если отношение R в множестве М обладает свойствами рефлексивности, симметричности и транзитивности, то оно называется отношением эквивалентности.
Отношения строгого порядка
Если отношение R в множестве М является транзитивным и ассиметричным и не является рефлексивным, то оно называется отношением строгого порядка. Пусть например, М = {1,2,3,4}. Тогда отношение «а больше b» имеет вид:
R = {(2,1),(3,1),(4,1),(3,2),(4,2),(4,3)}
Отношения не строгого порядка
Если отношение R в множестве М рефлексивно, антисимметрично и транзитивно, то оно называется отношением нестрогого порядка (используются так же термины: «отношение частичного порядка», «отношение квазипорядка», «отношение не полного порядка»).
7 Способы задания бинарных отношений и их основные свойства.
Всякое подмножество декартова произведения A×B называется бинарным отношением, определенным на паре множеств A и B (по латыни «бис» обозначает «дважды»). В общем случае по аналогии с бинарными можно рассматривать и n-арные отношения как упорядоченные последовательностиn элементов, взятых по одному из n множеств.
Для обозначения бинарного отношения применяют знак R. Поскольку R— это подмножество множества A×B, то можно записать R⊆A×. Если же требуется указать, что (a, b) ∈ R, т. е. между элементами a ∈ A и b ∈ B существует отношение R, то пишут aRb.
Способы задания бинарных отношений:
1. Это использование правила, согласно которому указываются все элементы, входящие в данное отношение. Вместо правила можно привести список элементов заданного отношения путем непосредственного их перечисления;
2. Табличный, в виде графов и с помощью сечений. Основу табличного способа составляет прямоугольная система координат, где по одной оси откладываются элементы одного множества, по второй — другого. Пересечения координат образуют точки, обозначающие элементы декартова произведения.
На (рисунке 1.16) изображена координатная сетка для множеств. Точкам пересечения трех вертикальных линий с шестью горизонтальными соответствуют элементы множества A×B. Кружочками на сетке отмечены элементы отношения aRb, где a ∈ A и b ∈ B, R обозначает отношение «делит».
Бинарные отношения задаются двухмерными системами координат. Очевидно, что все элементы декартова произведения трех множеств аналогично могут быть представлены в трехмерной системе координат, четырех множеств— в четырехмерной системе и т. д;
3. Способ задания отношений с помощью сечений используется реже, поэтому рассматривать его не будем.
8 Соответствия, отображения, функции.
Отношения соответствия
Понятие соответствия ясно интуитивно. Например, если требуется закодировать сообщение заменой букв алфавита их порядковыми номерами, то каждой букве необходимо поставить в соответствие определенное десятичное число. Если в кассе кинотеатра продают билеты на какой-либо сеанс, это значит, что каждому билету соответствует определенное место в зрительном зале. Если цветные карандаши упаковывают в коробки, то каждому набору цветных карандашей соответствует некоторая коробка, и т. д. Этот интуитивно ясный смысл вкладывается в слово «соответствие» и в том случае, когда говорят о каких-либо двух множествах.
В общем случае между элементами множеств A и B могут быть четыре вида соответствия в зависимости от того, один или несколько элементов множества A соответствуют элементу множества B и один или несколько элементов множества B ставятся в соответствие элементу множества A:
1) взаимно однозначное соответствие, когда каждому элементу a ∈ A ставится в соответствие единственный элемент b ∈ B и когда каждому элементу b ∈ B соответствует только один элемент a ∈ A. Например, если 33 буквы русского алфавита пронумеровать, то получим два множества A = {А, Б, В, …, Ю, Я} и B = {1, 2, 3,…, 32, 33}, между которыми существует взаимно однозначное соответствие. Взаимно однозначные соответствия называют биективными отображениями, или биекциями;
2) одно-многозначное соответствие, когда каждому элементу a ∈ A ставится в соответствие несколько (более одного) элементов множества B, но каждому элементу b ∈ B соответствует только один элемент a ∈ A. Примером может служить отношение: «a есть квадрат b». Пусть A = {1, 4, 9}, B = {–1, –2, –3, 1, 2, 3}. Тогда элементу 1 ∈ A ставится в соответствие два элемента 1 ∈ B и –1 ∈ B, поскольку 1 = 12 и 1 = (–1)2. То же самое относится и к элементам 4 ∈ A и 9 ∈A;
3) много-однозначное соответствие, когда для каждого элемента a ∈ A существует только один элемент b ∈ B, но каждому элементу множества B соответствует более одного элемента множества A. Примером может служить отношение «быть квадратным корнем», то есть «a есть квадратный корень числа b». Пусть A = {1, 2, 3, –1, –2, –3} и B = {1, 4, 9}. Тогда двум элементам 1 и –1 множества A соответствует один элемент 1 ∈ B, так как квадратным корнем из 1 является и 1 и –1. То же самое относится и к остальным элементам множеств A и B;
4) много-многозначное соответствие, когда каждому элементу a ∈ A соответствует более одного элемента множества B и каждому элементу b ∈ B соответствует также более одного элемента множества A. Примером много-многозначного соответствия может служить отношение вида «a не равно b», т. е. «a ≠ b». Допустим, что A={1, 2, 3}, B={2, 3, 4, 5}. Тогда элементу 1 ∈ A соответствуют элементы 2, 3, 4, 5 ∈ B, элементу 2 ∈ A — 3, 4, 5 ∈ B, элементу 3 ∈ A — 2, 4, 5 ∈ B. Аналогично: элементу 2 ∈ B соответствуют элементы 1, 3 ∈ A, элементу 3 ∈ B — 1, 2 ∈ A, элементу 4 ∈ B — 1, 2, 3 ∈ A, элементу 5∈B — 1, 2, 3 ∈ A.
Функциональные отношения. Отображения
Пусть даны множества X и Y. Бинарное отношение x R y является функциональным (функцией), если каждому элементу x ∈ X соответствует не более одного элемента y ∈ Y. . Из этого определения следует, что одно-многозначные и много-многозначные отношения функциональными быть не могут.
Для обозначения функции используются различные записи:
, f:X →Y ; f (x); (x, y) ∈ F, y = F(x), где F⊂ X×Y.
Значение функции y ∈ Y называют образом элемента x ∈ X, а сам элемент x ∈ X — прообразом. Множество X — это область определения функции, Y — область значений.
Функция y = F(x) называется всюду определенной, если каждому элементу x ∈ X соответствует один элемент y ∈ Y. В этом случае функцию называют также отображением (или инъекцией) множества X в множество Y. Функция являетсянедоопределенной (частично определенной), если имеется хотя бы один элемент x ∈ X, которому не соответствует никакой элемент y ∈ Y. Отсюда следует, что недоопределенные функции отображениями не являются.
Рассмотрим несколько примеров.
Пример 1. Пусть даны два множества:
|
|
X = {а, б, в, г, д, е}; Y = {1, 2, 3, 4}. |
(1.27) |
Выделим в множестве X×Y подмножество вида:
F = {(а, 1), (б, 3), (в, 4), (г, 2), (д, 2), (е, 3)}.
Первый элемент каждой пары множества F — это элемент множества X, второй — элемент множества Y. Все первые элементы различны, следовательно, каждому значению x ∈ X соответствует точно один элемент y ∈ Y. Это значит, что множество F представляет собой функциональное отношение и, следовательно, является отображением множества X в множество Y.
Пример 2. Выделим в декартовом произведении множеств (28) множество вида:
M = {(а, 1), (а, 2), (б, 3), (в, 4), (г, 3), (д, 2), (е, 4)}.
В это множество входят пары (а, 1) и (а, 2), у которых первые элементы одинаковы. Что это значит? Очевидно, то, что элементу а ∈ X соответствуют два элемента множества Y: 1 ∈ Y и 2 ∈ Y. Но по определению функционального отношения каждому элементу множества X может соответствовать не более одного элемента множества Y. Следовательно, отношение, представленное множеством M, не является функцией.
Пример 3. Пусть X={1, 2, 3, 4}, Y={а, б, в} и пусть отношение F имеет вид «буквам русского алфавита ставятся в соответствие их порядковые номера», т. е.:
|
|
. |
(1.28) |
Элементу 4 ∈ X в множестве Y не соответствует никакой элемент, следовательно, отношение (29) есть не полностью определенная функция. Расширим область определения функции, заменив множество {а, б, в} множеством {а, б, в, г}, тогда получим:
.
Теперь функция является всюду определенной.
Пример 4. Пусть дано выражение:
|
|
. |
(1.29) |
Известно, что, например, и , так как 32 = 9 и (–3)2= 9, т. е. одному и тому же значению x соответствуют два различных значения y. Следовательно, по определению выражение (30) функцией не является. Если же ограничиться только неотрицательными числами, то выражение (30) является функцией с областью определения и областью значений в множестве неотрицательных чисел.
9 Взаимнооднозначные соответствия и мощности множеств.
Отношения соответствия.
В общем случае между элементами множеств А и В могут быть четыре вида соответствия в зависимости от того, один или несколько элементов множества А соответствуют элементу множества В и один или несколько элементов множества В ставятся в соответствие элементу А:
Взаимно
однозначное соответствие, когда каждому
элементу
ставится в соответствие единственный
элемент
и когда каждому элементу
соответствует только один элемент
.
Одно-многозначное
соответствие, когда каждому элементу
ставится в соответствие несколько
(более одного) элементов множества В,
но каждому элементу
соответствует
только один элемент
.
Много-однозначное
соответствие, когда для каждого элемента
существует только один элемент
,
но каждому элементу множества В
соответствует более одного элемента
множества А.
Много-многозначное
соответствие, когда каждому элементу
соответствует более одного элемента
множества В и каждому элементу
соответствует также более одного
элемента множества А.
Счетные множества.
Множество, равномощное множеству всех натуральных чисел, называется счетным.
Мощность
счетного множества обозначается символом
читается: алеф нуль. Алеф первая буква
финикийского (древнесемитского) алфавита.
10 Счетные множества, теоремы о счетных множествах.
Существует два подхода к понятию бесконечности. Основой первого является актуальная бесконечность, второго —потенциальная. В первом случае бесконечность рассматривается как множество, содержащее бесконечно много элементов, но при этом предполагается, что оно задано в готовом, сформированном виде и его можно представить как некоторый объект. Именно так представлял себе бесконечное множество Г. Кантор.
Потенциальная же бесконечность рассматривается не как нечто завершенное, а как процесс, у которого нет последнего шага, как процесс непрерывного увеличения числа элементов.
В случае бесконечных множеств прямое перечисление элементов исключено, поэтому задавать их можно только описанием признаков, характерных для элементов данного множества. Например:
A = {x / x — натуральное число, x > 1, x — число, делящееся только на себя и на единицу}.
Согласно этой записи элементами множества A являются простые числа, причем количество их не ограничено, вследствие чего множество A надо считать бесконечным (поскольку доказано, что количество простых чисел бесконечно велико).
В теории бесконечных множеств широко используются понятия натурального числа и натурального ряда.
«Натуральные числа — числа, возникающие в процессе простого счета, целые положительные числа 1, 2, 3, …». В дальнейшем во избежание неопределенности будем считать, что число 0 натуральным не является и что натуральный ряд начинается с единицы: 1, 2, 3, 4, 5, … .
Множество, равномощное множеству всех натуральных чисел, называется счетным. Согласно этому определению всякое бесконечное множество является счетным, если найдется способ показать, как нумеровать его элементы.
Мощность счетного множества обозначается символом ℵ0, читается: алефнуль. Алеф — первая буква финикийского (древнесемитского) алфавита.
Например, если E — счетное множество, то |E| = ℵ0.
Приведем некоторые теоремы о счетных множествах.
Теорема 1. Всякое бесконечное множество содержит счетное подмножество.
Теорема 2. Всякое бесконечное подмножество счетного множества счетное.
Теорема 3. Множество всех целых чисел счетное.
Теорема 4. Объединение счетного множества A и конечного множества B счетное.
Теорема 5. Объединение конечного множества счетных множество счетное.
Теорема 6. Декартово произведение двух счетных множеств A и B счетное.
Теорема 7. Объединение счетного множества счетных множеств A, B, C, … счетное.
Теорема 8. Множество всех рациональных чисел счетное.
Рациональными называют все положительные и отрицательные дроби вида P/ q, где P и q — натуральные числа. К рациональным относятся все целые положительные и отрицательные числа, а также нуль.
Теорема 9. Множество всех алгебраических чисел счетное.
Алгебраическими называются числа, являющиеся корнями уравнения:
,
где a0, a1, a2, …, an — целые числа (т. е. они могут быть положительными, отрицательными и равными нулю).
Числа, которые не являются алгебраическими, называются трансцендентными.
11 Множества мощности континуума. Теорема Кантора.
Получим
матрицу, содержащую четное множество
строк, в каждой из которых бесконечное
число десятичных цифр. Допустим, что в
матрице нет не одной пары равных между
собой чисел. Все ли действительные числа
окажутся в матрице? Нет, не все. Чтобы
убедится в этом воспользуемся диагональным
методом, разработанным Г. Кантором, и
найдем число, которое соответствует
матрице, т.е. оказалось незанумерованным.
Суть метода Г. Кантора применительно к
данному случаю состоит в следующем.
Если в первом числе первая после запятой
цифра (цифра
)
не равна, например, 3, то в искомое число
после запятой записываем цифру 3. Если
же
=3,
то записываем, допустим 2. Переходя ко
второму числу матрицы. Если
,
то записываем на втором месте искомого
числа цифру 3. Если
,
то записываем число 2. Перейдя к третьему
числу, записываем искомое число 3, если
и т.д. Очевидно что получившееся число
отсутствует в списке, так как оно
отличается от первого числа после
запятой цифрой, от второго числа
отличается цифрой от третьего – третьей
и т.д. Таким образом полученное число
отсутствует в списке, но принадлежит
множеству действительных чисел интервала
.
Полученное число не является единственным отсутствующим в списке. Достаточно вместо цифры 3 и 2 взять какие-нибудь другие и мы получим еще одно число. Даже если найденные числа включит в общий список, то и в расширенном списке будут находится не занумерованные числа.
Так
как мощность булеана В(Е) равна мощности
множества всех действительных чисел
интервала
,
то эти множества эквивалентны. Они
являются несчетными и оба характеризуются
кардинальным числом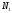
.
Такие множества условно называют
-множествами.
Мощность
континуума – не самая большая мощность
среди бесконечных множеств. Что бы
убедится в этом воспользуемся двоичными
числами, так же как и в случае с счетными
множествами. Поставим в соответствие
каждому элементу
-множества
двоичный разряд. Если единица в числе
обозначает вхождение элемента в
подмножество, а нуль – отсутствие
элемента в данном подмножестве, то
каждому двоичному числу будет
соответствовать некоторое подмножество
-множества.
Мощность множества таких подмножеств
обозначается буквой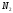
,
очевидно, что
Откуда
следует что мощность булеана
-множества
превышает мощность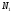
-множества
.
Точно так же можно утверждать, что
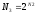
То
есть мощность
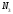-множества
превышает мощность булеана
-множества.
Далее по аналогии получаем :
,
,
,…,
,…
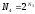Откуда следует, что множества с наибольшей мощностью не существует.
В завершение подраздела приведем одну теорему о множествах мощности континуума: объединение множества мощности континуума и счетного множества имеет мощность континуума.
12 Элементы теории нечетких множеств.
Под нечётким множеством A понимается совокупность
,
где Х — универсальное множество, а
— функция принадлежности (характеристическая
функция), характеризующая степень
принадлежности элемента
нечёткому множеству А .
Функция
принимает значения в некотором вполне
упорядоченном множествеМ.
Множество М
называют
множеством принадлежностей, часто в
качестве М
выбирается отрезок
. Если
,
то нечёткое множество может рассматриваться
как обычное, чёткое множество.