гос / Theme1

Прикладная теория цифровых автоматов. Тема №1

БУЛЕВА (ПЕРЕКЛЮЧАТЕЛЬНАЯ) ФУНКЦИЯ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. ОСНОВНЫЕ ЗАКОНЫ И ТОЖДЕСТВА БУЛЕВОЙ АЛГЕБРЫ

∙Матричный (табличный).

∙Аналитический.

∙Геометрический.

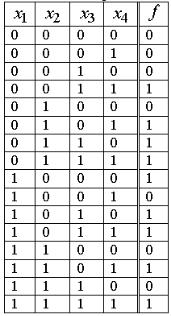
При матричном способе булева функция f (x1, x2 ,..., xn ) задается таблицей истинности (табл. 1.1, 1.2), в левой части которой указываются все двоичные наборы длины n , а в правой – значения функции на этих наборах.

Под двоичным набором α1,α2 ,...,αn понимается совокупность значений аргументов x1, x2 ,..., xn функции f . В таблицах 1.1 и 1.2 перечислены все двоичные наборы соответственно длины 3 и 4.

Таблица 1.1 – Произвольная функция 3-х переменных

Прикладная теория цифровых автоматов. Тема №1

Таблица 1.2 – Произвольная функция 4-х переменных

Очевидно, что количество двоичных наборов функции n аргументов равно

2n .

Иногда двоичные наборы в таблице истинности булевой функции удобно представлять номерами наборов. Если рассматривать двоичный набор как число в канонической двоичной системе счисления с естественным порядком весов, то, переведя это число в десятичную систему счисления, можно получить номер набора. Перевод числа из двоичной системы счисления в десятичную осуществляется по формуле:

011 = 0 × 22 +1× 21 +1× 20 = 3

100= 1× 22 + 0 × 21 + 0 × 20 = 4

101= 1× 22 + 0 × 21 +1× 20 = 5

110= 1× 22 +1× 21 + 0 × 20 = 6

111= 1× 22 +1× 21 +1× 20 = 7

Прикладная теория цифровых автоматов. Тема №1

При использовании номеров наборов булеву функцию можно представить указанием номеров наборов, на которых функция принимает единичное (или нулевое) значение.

Пример 1.2 Представить булеву функцию, заданную таблицей истинности (табл. 1.1) с помощью указания номеров наборов, на которых функция принимает единичное значение и нулевое значение.

Для единичных значений функции: f (x1, x2 , x3 ) = {1, 2, 3, 5, 6}.

Для нулевых значений функции: f (x1, x2 , x3) = {0, 4, 7}.

Горизонтальная черта над функцией обозначает операцию инверсии

(операцию НЕ).

При больших значениях n задавать булеву функцию с помощью таблицы истинности неудобно в силу громоздкости последней. В таком случае используют модификацию таблицы истинности – матрицу.

Для построения такой матрицы множество из n переменных разбивают на два подмножества: x1, x2 ,..., x j −1 и x j , x j +1,..., xn . Переменными x1, x2 ,..., x j −1

отмечают строки таблицы, задавая в каждой строке значение соответствующего двоичного набора длины j −1. Переменными x j , x j +1,..., xn отмечают столбцы таблицы, задавая в каждом столбце значение соответствующего двоичного набора длины n − j +1. Значение функции указывается в клетке на пересечении соответствующей строки и столбца.

Пример 1.3 Представить функцию, заданную таблицей истинности

(табл. 1.2) с помощью матрицы 4 ×4 .

Матрица функции представлена в таблице 1.3.

Таблица 1.3 – Матрица функции 4-х переменных

Прикладная теория цифровых автоматов. Тема №1

При геометрическом способе булева функция f (x1, x2 ,..., xn ) задается с помощью n -мерного куба. В геометрическом смысле каждый двоичный набор есть n -мерный вектор, определяющий точку n -мерного пространства. Отмечая точками вершины куба, в которых функция принимает единичное (либо

нулевое) значение, можно получить геометрическое представление функции.

При аналитическом способе булева функция задается формулами, то есть аналитическими выражениями, построенными на основе операций булевой алгебры. Аналитический способ задания булевой функции занимает особое место в проектировании цифровых автоматов. Фактически все преобразования над булевыми функциями, необходимые для построения цифрового автомата,

ведутся на аналитическом уровне.

Определение 1.2 Булеву функцию, определенную на всех двоичных наборах, называют полностью определенной. Если же функция определена не на всех двоичных наборах, то ее называют частично определенной или

частичной. Неопределенные значения функции в таблице истинности обычно

Прикладная теория цифровых автоматов. Тема №1

Таблица 1.5 – Элементарные функции двух переменных f (x1, x2 )

Указанные в таблицах 1.4 и 1.5 функции позволяют строить новые булевы функции с помощью обобщенной операции, которая называется операцией

суперпозиции. Эта операция заключается в подстановке одних булевых функций в качестве аргументов других. Например, если подставить f2 (x3, x4 ) и f3 = x5 соответственно вместо аргументов x1 и x2 булевой функции f1(x1, x2 ) ,

то получим функцию f1( f2 (x3, x4 ), x5 ) , которая является функцией 3-х

переменных x3, x4 , x5 и не зависит уже от переменных x1 и x2 .

Прикладная теория цифровых автоматов. Тема №1

Элементарной булевой функции соответствует реализующий ее элемент, а

суперпозиции функций – соединение элементов.

Для булевой алгебры определены три операции:

1.отрицание (НЕ);

2.конъюнкция (И);

3.дизъюнкция (ИЛИ).

Вэтой алгебре справедливы 3 аксиомы:

1.Закон коммутативности: x + y = y + x; xy = yx .

2.Закон ассоциативности: (x + y) + z = x + ( y + z); (xy)z = x( yz) .

3.Закон дистрибутивности: x( y + z) = xy + xz; x + yz = (x + y)(x + z) .

Следует отметить, что теоремы де Моргана в силу коммутативности и ассоциативности конъюнкции и дизъюнкции применимы для нескольких переменных:

x1 + x2 + ... + xn = x1 × x2 ×...× xn x1 × x2 ×...× xn = x1 + x2 + ... + xn

Прикладная теория цифровых автоматов. Тема №1

СПИСОК ЛИТЕРАТУРЫ

1.Самофалов К. Г. и др. Прикладная теория цифровых автоматов. – К. : Вища шк. Головное изд-во, 1987. – 375 с.

2.Савельев А. Я. Прикладная теория цифровых автоматов: Учебник для вузов. – М.: Высш. шк., 1987. – 272 с.: ил.

3.Савельев А. Я. Арифметические и логические основы цифровых автоматов: Учебник. – М.: Высш. шк., 1980. – 255 с.: ил.

4.Поспелов Д. А. Логические методы анализа и синтеза схем. Изд. 3-е,

перераб. и доп. – М.: «Энергия», 1974. – 368 с.: ил.

– 128 с.: ил.

7.Потемкин И. С. Функциональные узлы цифровой автоматики. – М.:

Энергоатомиздат, 1988. – 320 с.: ил.

8.Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. – М.: Наука, 1966. – 119 с.: ил.