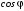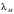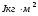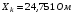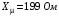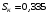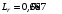ДИПЛОМ / 3 Статика
.docx
 3
ДОСЛІДЖЕННЯ СТАТИЧНИХ РЕЖИМІВ РОБОТИ
АВТОМАТИЗОВАНОГО ЕЛЕКТРОПРИВОДУ
ЛІФТОВОЇ УСТАНОВКИ
3
ДОСЛІДЖЕННЯ СТАТИЧНИХ РЕЖИМІВ РОБОТИ
АВТОМАТИЗОВАНОГО ЕЛЕКТРОПРИВОДУ
ЛІФТОВОЇ УСТАНОВКИ
3.1 Розрахунок потужності двигуна ліфтової установки
Розрахунок потужності слід розпочинати з аналізу діаграми неврівноваженості рухомих частин ліфту, яка будується по всій висоті підйому кабіни.
Неврівноваженість рухомої частини системи не залежить від напрямку руху кабіни, а змінюється по висоті майже по лінійному закону.
Неврівноваженість визначається при навантаженій номінальним вантажем та не навантаженій кабіні для нижньої і верхньої відміток її зупинки, які розраховуються за формулами:
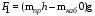 ;
(3.1)
;
(3.1)
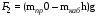 ;
(3.2)
;
(3.2)
де
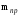 –
вага противаги, кг;
–
вага противаги, кг; –
вага кабіни;
–
вага кабіни;
В нашому випадку вага кабіни не змінюється, тому розрахунок буде проводитися тільки при ненавантаженій кабіні для нижньої і верхньої відміток її зупинки.
Дані для розрахунку наведені в таблиці 3.1
Таблиця 3.1 – Технічні дані підйомника
|
Швидкість підйому, м/с |
0,8 |
ККД лебідки |
0,6 |
|
Номінальна вантажопідйомність, кг |
49 |
Радіус барабана, м |
0,12 |
|
Вага кабіни, кг |
68,6 |
Висота підйому, м |
2,25 |
|
Вага противаги, кг |
98 |
Число циклів через, год |
20 |
Підставивши їх у формули отримаємо:
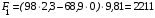 Н;
Н;
 Н;
Н;
Тепер відмічаємо на діаграмі неврівноваженості (рис 3.1) отримані результати.
Отримана
діаграма має дві ділянки
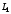 ,
,
 .
Кожна з них характеризується середньою
неврівноваженістю
.
Кожна з них характеризується середньою
неврівноваженістю
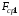 та
та
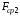 .
.
Визначаємо,
що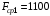 ;
;
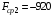 .
.
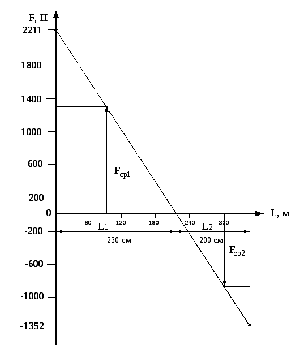
Рисунок 3.1 – Діаграма неврівноваженості ліфту
Далі визначаємо статичне навантаження ліфту за формулою:
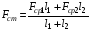 ;
(3.3)
;
(3.3)
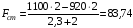 Н;
Н;
Визначивши статичне навантаження визначаємо статичну потужність:
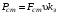 ;
(3.4)
;
(3.4)
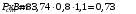 ;
;
де
 –
швидкість підйому кабіни,
–
швидкість підйому кабіни,
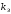 –
коефіцієнт запасу, приймається (1,1-1,2).
–
коефіцієнт запасу, приймається (1,1-1,2).
Далі слід уточнити потужність з врахуванням тривалості включення ліфта:
 ;
(3.5)
;
(3.5)
де
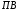 – фактична тривалість включення,
– фактична тривалість включення,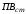 –
найближча фактична тривалість включення
по стандартному ряду,
–
найближча фактична тривалість включення
по стандартному ряду,
 –
відношення постійних втрат двигуна до
змінних.
–
відношення постійних втрат двигуна до
змінних.
Так, як розглядається лабораторний стенд то приймемо, що:
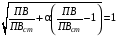 ;
;
Тоді формула врахування тривалості включення ліфта буде мати вигляд:
 ;
(3.6)
;
(3.6)
Далі підставляємо числа:

Відповідно до розрахованої потужності обираємо АД з к.з ротором серії 4А80А6, технічні дані якого наведені в таблиці 3.2.
Таблиця 3.2 – Технічні дані обраного двигуна
|
Номінальна напруга
живлення
|
380 |
|
Номінальна потужність
|
0,75 |
|
Номінальне ковзання
|
0,084 |
|
|
916 |
|
Номінальний
струм
|
2,23 |
|
Опір статора |
12,2 |
|
Опір ротора
|
8,8 |
|
Індуктивний опір
статора
|
11,8 |
|
Індуктивний опір
ротора
|
10,7 |
|
КПД
|
0,69 |
|
Коефіцієнт потужності
|
0,74 |
|
Кратність пускового
струму
|
4 |
|
Кратність пускового
моменту
|
2 |
|
Кратність максимального
моменту
|
2,2 |
|
|
0,00310 |
|
Число пар полюсів р |
3 |
3.2 Розрахунок параметрів схеми заміщення АД
Враховуючи специфіку розрахунку параметрів АД, застосовують Т – подібну схему заміщення (рис. 3.2), в якій нехтують активним опором ланцюга намагнічування. Розрахунок параметрів даної схеми заміщення аналогічний розрахунку Г – образної схеми.
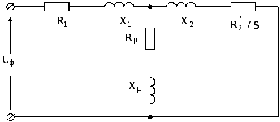
Рисунок 3.2 – Т-подібна схема заміщення АД
Одними з основних параметрів, що характеризують номінальний режим асинхронного двигуна, є номінальні значення наведеного струму ротора і намагнічує струму.
Враховуючи
те, що при переході від ідеального
холостого ходу
 до номінального режиму
до номінального режиму
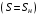 магнітний потік практично не змінюється,
приймаємо
магнітний потік практично не змінюється,
приймаємо
 рівним струму холостого ходу
рівним струму холостого ходу
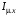 ,
,
Вимірювання при роботі двигуна без навантаження на валу.
Визначимо
значення
 ,
,
 використовуючи паспортні дані
наведені в таблиці 3.2, номінального
струму статора
використовуючи паспортні дані
наведені в таблиці 3.2, номінального
струму статора
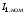 ,
кратності максимального моменту
,
кратності максимального моменту
 ,
та номінального коефіцієнта потужності
,
та номінального коефіцієнта потужності
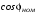 .
.
На підставі векторної діаграми і основних співвідношень АД, а також враховуючи рівняння для критичного ковзання.
 ;
(3.7)
;
(3.7)
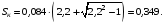


де
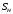 –
номінальне ковзання АД,
–
номінальне ковзання АД,
 –
кратність максимального моменту.
–
кратність максимального моменту.
Визначення номінального значення наведеного струму ротора:
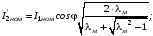 (3.8)
(3.8)
 A
A
Визначення струму намагнічування:
 ;
(3.9)
;
(3.9)
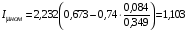 A
A
Визначимо відсутні дані АД по Т- подібній схемі заміщення (рис 3.2), паспортні дані якого наведені в таблиці 3.2.
Визначимо індуктивний опір короткого замикання з виразу для критичного ковзання.
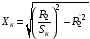 ;
(3.10)
;
(3.10)
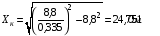
Індуктивний опір контуру намагнічування:
 ;
(3.11)
;
(3.11)
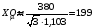
Індуктивність намагнічування:
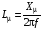 ;
(3.12)
;
(3.12)
де
 – частота напруги живлення,
– частота напруги живлення,
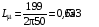
Індуктивність фази статора:
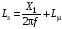 ;
(3.13)
;
(3.13)
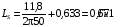
Індуктивність фази ротора:
 ;
(3.14)
;
(3.14)

Використовуючи паспортні дані можна визначити номінальні втрати двигуна, знаючи ККД і активний опір обмоток.
Додаткові втрати в статорі:
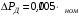 ,
(3.15)
,
(3.15)

Втрати в обмотці статора і додаткові втрати:
 ;
(3.16)
;
(3.16)
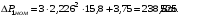
Механічні втрати рівні:
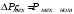 ;
(3.17)
;
(3.17)
де
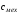 – коефіцієнт механічних втрат,
приймаємо 1% от
– коефіцієнт механічних втрат,
приймаємо 1% от ,
,
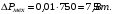
Втрати в роторі:
 ;
(3.18)
;
(3.18)
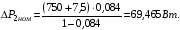
Сумарні втрати двигуна:
 ,
(3.19)
,
(3.19)
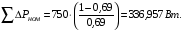
Втрати в сталі статора:
 ,
(3.20)
,
(3.20)
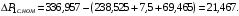
Дані розрахунків зведено в таблицю 3.3
Таблиця 3.3 – Розрахункові параметри АД
|
Індуктивний опір розсіювання |
|
|
Опір намагнічування |
|
|
Критичне ковзання двигуна |
|
|
Індуктивність намагнічування |
|
|
Індуктивність фази статора |
|
|
Індуктивність фази ротора |
|
3.3 Аналіз статичних електромеханічних характеристик ЕП ліфта при зміні частоти обертання
Як зазначалося раніше, при розрахунку властивостей і характеристик системи асинхронний двигун – перетворювача частоти, застосовується Т – подібна схема заміщення, що дозволяє враховувати вплив контуру намагнічування. При аналізі та розрахунках даної схеми заміщення використовуються такі позначення.
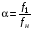 ,
(3.21)
,
(3.21)
Відносна частота статора:
 ,
(3.22)
,
(3.22)
параметр абсолютного ковзання, або відносна частота ротора.
Параметр β використовується замість ковзання s і пов'язаний з ним співвідношенням:
 .
(3.23)
.
(3.23)
З формули визначимо взаємозв'язок між абсолютним ковзанням β та кутовою швидкістю обертання ω1 двигуна:
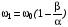 ,
,
де ω0– кутова швидкість обертання поля статора.
Відносна напруга:
 ,
(3.24)
,
(3.24)
Виходячи з частотного закону управління електроприводом:
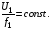 (3.25)
(3.25)
визначимо взаємозв’язок між α и γ, як:
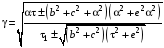 .
(3.26)
.
(3.26)
Коефіцієнт розсіювання відповідно для статора і ротора:
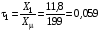 і
і
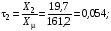 .
.
Загальний коефіцієнт розсіювання:
 ;
(3.27)
;
(3.27)

Введемо позначення:
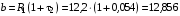 ,
,
 ,
,
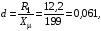
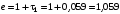 .
.
З розрахунку схеми заміщення отримуємо:
– cтрум статора:
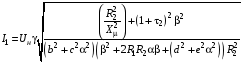 ;
(3.28)
;
(3.28)
– наведений струм ротора:
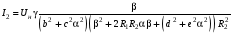 ;
(3.29)
;
(3.29)
– електромагнітний момент двигуна:
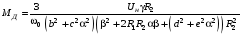 .
(3.30)
.
(3.30)
Переймаючи значення абсолютного ковзання
 в межах від 0 до 1 і виконуючи розрахунок
за формулами, наведеними вище, отримаємо
сімейство статичних характеристик
двигуна для частот (50, 40, 30, 20) Гц:
в межах від 0 до 1 і виконуючи розрахунок
за формулами, наведеними вище, отримаємо
сімейство статичних характеристик
двигуна для частот (50, 40, 30, 20) Гц:
З урахуванням перевантажувальної за струмом спроможності перетворювача частоти (табл.2.1), що дорівнює 5,1 А, отримаємо з рис. 3.3 значення кутової частоти обертання. З урахуванням останнього та істотної механічної характеристики системи ПЧ-АД отримаємо максимальне значення моменту, що зображено на рис 3.5. Отримані результати задовольняють нашим вимогам до перетворювача частоти.
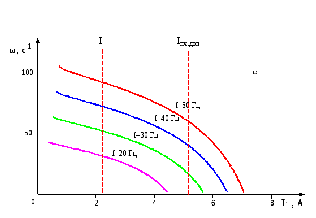
Рисунок 3.3 – Залежність кутовий частоти обертання від струму статора при зміні частоти живлячої напруги
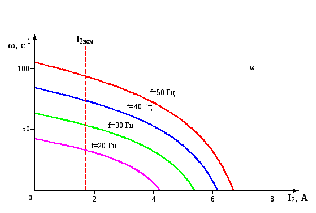
Рисунок 3.4 – Залежність кутовий частоти обертання від струму ротора при зміні частоти живлячої напруги

Рисунок 3.5 – Сімейство механічних характеристик електроприводу
До основних енергетичних показників роботи електроприводів відносяться втрати потужності, втрати енергії, ККД, потужності cosφ. Визначальним для АД є втратив міді статора і ротора, втрати в сталі статора від гістерезису і вихрових струмів, а також механічні втрати. Основними втратами в сталі можна знехтувати, тому що при абсолютному ковзанні, яке не перевищує номінального, вони дуже малі. В сумі всі додаткові втрати представляють в середньому 1% від споживаної двигуном потужності.
Згідно енергетичної діаграмі асинхронного двигуна його двигуна; електромагнітний ККД можна обчислити за формулою:
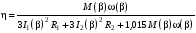 ;
(3.31)
;
(3.31)
На рисунку 3.6 наведені статичні енергетичні характеристики системи ПЧ-АД для різної частоти живильної мережі.

Рисунок 3.6 – Залежність ККД від потужності АД при зміні частоти живлячої напруги
Аналіз кривих (рис. 3.6) дозволяє сказати, що при досить широкому діапазоні зміни моменту двигуна, а відповідно і частоти обертання двигуна, ККД залишається на рівні максимального.
Висновки за розділом:
В третьому розділі дипломної роботи
був проведений розрахунок потужності
двигуна ліфтової установки та згідно
з результатами розрахунку обрано АД з
к.з. ротором серії 4А80А6, також були
розраховані параметри схеми заміщення
і номінальні втрати двигуна та по
отриманим даним проведений аналіз
статичних електромеханічних характеристик
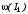 ,
,
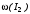 ,
,
 ,
, ЕП ліфта при зміні частоти обертання.
ЕП ліфта при зміні частоти обертання.

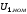 В
В кВт
кВт %
%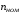 об/хв
об/хв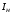
 Ом
Ом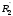 Ом
Ом Ом
Ом Ом
Ом ,
%
,
%