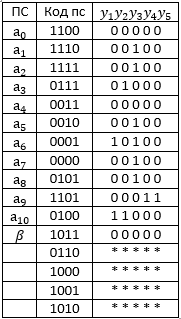
Далі будуємо таблицю виходів автомата Мура.
Таблиця 2.2. – Таблиця виходів автомата Мура

КП.2015.ФЕКІ.102.043.002.ПЗ 7 КП.2015.ФЕКІ.102.043.002.ПЗ 7
Мінімізую Y1
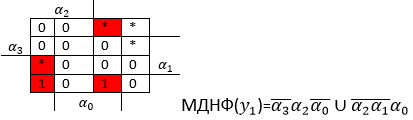
Мінімізую Y2
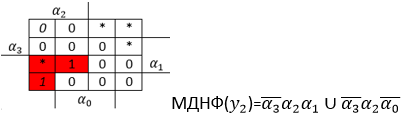
Мінімізую Y3
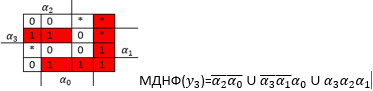
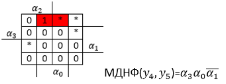
 Мінімізую
Y4
та Y5
Мінімізую
Y4
та Y5
|
|
КП.2015.ФЕКІ.102.043.003.Е3




КП.2015.ФЕКІ.102.043.003.Е3
Автомат
керуючий.
Схема електрична функціональна Шеврін
В.В. Юдіна
А.Л.
2.3 Реалізація системи булевих функцій f1,f2,f3 на плм
Виконуємо мінімізацію функцій f1,f2,f3, наведених у таблиці 1.1, методом діаграм Вейча:
F1 F2 F3

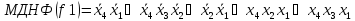
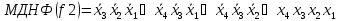
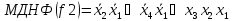
Реалізую мінімізовані функції на (n, p, k) – ПЛМ, де n=4 – кількість входів, p=3 – кількість виходів, k=9 – кількість кон’юнкцій.
Площа S=k*(n+p)= 63
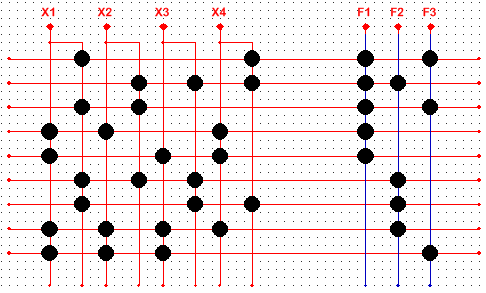
Рисунок 2.5. – Реалізація функцій на ПЛМ

2.4 Представлення булевої функції в різних базисах
Представимо функцію f4 в канонічних формах різних базисів:
Базис Буля(І\АБО):
F=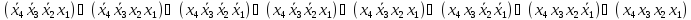
Базис Шефера (І-НІ\І-НІ)
F=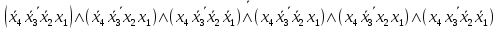
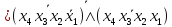
Базис Пірса (АБО-НІ\АБО-НІ)
F=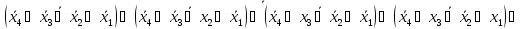
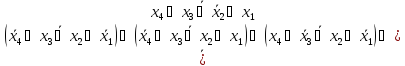
Алгебра Жегалкіна
F=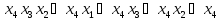
Визначаємо приналежність функції до класів:
Так як на наборах 0000 та 1111 функція дорівнює 0 та 1 відповідно, то ця функція є зберігаючою константу 0 та 1.
В результаті переведення функції у алгебру Жегалкіна операція кон’юнкції залишилась, що свідчить про те, що функція не є лінійною.
Функція є немонотонною, оскільки на сусідніх наборах не зберігається правило монотонності.
Функція не самодвійчаста, так як на деяких протилежних наборах значення функції не протилежні.
 Мінімізація
функції.
Мінімізація
функції.
Метод невизначених коефіцієнтів:
|
X1 |
X2 |
X3 |
X4 |
F |
1 |
2 |
3 |
4 |
12 |
13 |
14 |
23 |
24 |
34 |
123 |
124 |
134 |
234 |
1234 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
00 |
00 |
00 |
00 |
00 |
00 |
000 |
000 |
000 |
000 |
0000 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
00 |
00 |
01 |
00 |
01 |
01 |
000 |
001 |
001 |
001 |
0001 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
00 |
01 |
00 |
01 |
00 |
10 |
001 |
000 |
010 |
010 |
0010 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
00 |
01 |
01 |
01 |
01 |
11 |
001 |
001 |
011 |
011 |
0011 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
01 |
00 |
00 |
10 |
10 |
00 |
010 |
010 |
000 |
100 |
0100 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
01 |
00 |
01 |
10 |
11 |
01 |
010 |
011 |
001 |
101 |
0101 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
01 |
01 |
00 |
11 |
10 |
10 |
011 |
010 |
010 |
110 |
0110 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
01 |
01 |
01 |
11 |
11 |
11 |
011 |
011 |
011 |
111 |
0111 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
10 |
10 |
10 |
00 |
00 |
00 |
100 |
100 |
100 |
000 |
1000 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
10 |
10 |
11 |
00 |
01 |
01 |
100 |
101 |
101 |
001 |
1001 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
10 |
11 |
10 |
01 |
00 |
10 |
101 |
100 |
110 |
010 |
1010 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
10 |
11 |
11 |
01 |
01 |
11 |
101 |
101 |
111 |
011 |
1011 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
11 |
10 |
10 |
10 |
10 |
00 |
110 |
110 |
100 |
100 |
1100 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
11 |
10 |
11 |
10 |
11 |
01 |
110 |
111 |
101 |
101 |
1101 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
11 |
11 |
10 |
11 |
10 |
10 |
111 |
110 |
110 |
110 |
1110 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
11 |
11 |
11 |
11 |
11 |
11 |
111 |
111 |
111 |
111 |
1111 |
МДНФ4=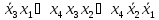
Mетод Квайна-Мак-Класкі:
|
Група |
|
|
|
|
1 |
0001 |
00-1 |
-0-1 |
|
1000 |
-001 |
-0-1 | |
|
2 |
0011 |
100- |
|
|
1001 |
1-00 |
| |
|
1100 |
-011 |
| |
|
3 |
1011 |
10-1 |
|
|
1110 |
11-0 |
| |
|
4 |
1111 |
1-11 |
|
|
111- |
|
|
|
0001 |
1000 |
0011 |
1001 |
1100 |
1011 |
1110 |
1111 |
|
100- |
|
* |
|
* |
|
|
|
|
|
1-00 |
|
* |
|
|
* |
|
|
|
|
11-0 |
|
|
|
|
* |
|
* |
|
|
1-11 |
|
|
|
|
|
* |
|
* |
|
111- |
|
|
|
|
|
|
* |
* |
|
-0-1 |
* |
|
* |
* |
|
* |
|
|
МДНФ4=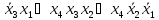
 Метод
діаграм Вейча:
Метод
діаграм Вейча:
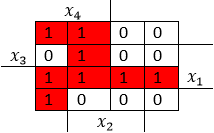
МДНФ4=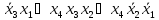
Метод Блейка-Порецького:
 МДНФ4=
МДНФ4=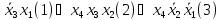
1:3 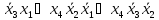
2:3 
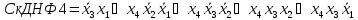
Результати усіх методів сходяться.

Висновки
Під час виконання курсового проекту був проведений синтез цифрового автомату Мура, який працює за вказаним алгоритмом. Були побудовані граф – схеми алгоритму роботи автомату, проведена мінімізація функцій збудження тригерів та функцій видачі сигналів. Після цього в середовищі Multisim в заданому базисі була побудована функціональна схема роботи автомату. Також була проведена мінімізація системи часткого визначених функцій для реалізація ПЛМ. Після чого 4-ма методами була проведена мінімізація заданої функції. Функція була представлена в різних базисах та алгебрі Жегалкіна. Було визначено приналежність даної функції до 5 визначних класів.
2.6 Список літератури
Конспект лекцій з дисципліни «Компьютерна логіка», 2015р.
В.И. Жабин, В.В. Ткаченко Логические основы и схемотехника цифровых ЭВМ. – Киев: ТОО “ВЕК +”б 1999г.
К.Г. Самофалов Цифровые ЭВМ. Практикум. – Киев: Высшая школа, 1989г.
Савельев А.Я. Арифметические и логические основы цифровых автоматов. – Москва: Высшая школа, 1986г.