Baza_zapitan-_TJMS_MS_-07_12_15_zashifr

КОМПЛЕКТ ТЕСТОВИХ ЗАВДАНЬ

з дисципліни «Теорія ймовірностей та математична статистика»,

напрям «Комп’ютерна інженерія»

Математична статистика і ймовірнісні процеси

Затверджено на засіданні кафедри КІС

Протокол №__04__ від „_04_” _12_ 2015 року

Завідувач кафедри

____________________ Луговой А. В.

(підпис)

Екзаменатор ____________________ Сидоренко В. М.

( підпис)

1.Математична статистика, це:

а) це наука, яка вивчає ймовірності випадкових явищ;

б) це наука, яка вивчає ймовірності випадкових явищ, що задовольняють умовам статистичної стійкості;

в) це наука про математичні методи, які дозволяють за вибірковими даними будувати ймовірнісну модель явища, що вивчається;

г) це наука, яка вивчає ймовірності випадкових величин, що задовольняють умовам статистичної стійкості.

2. Генеральна сукупність це:

а) множина всіх можливих значень, що може приймати неперервна випадкова величина;

б) множина всіх можливих значень, що може приймати дискретна випадкова величина;

в) множина всіх можливих значень, що може приймати випадкова величина;

г) набір декількох можливих значень, що може приймати випадкова величина.

3. Вибірка це:

а) половина значень, відібраних з генеральної сукупності;

б) декілька значень, відібраних з генеральної сукупності;

в) чверть значень, відібраних з генеральної сукупності;

г) декілька цілих значень, відібраних з генеральної сукупності;

4. Статистична гіпотеза це:

а) припущення щодо закону розподілу випадкової величини;

б) припущення щодо значень параметрів випадкової величини;

в) припущення щодо репрезентативності вибірки;

г) припущення щодо рівня надійності статистичних висновків.

5. Нульовою статистичною гіпотезою називається гіпотеза:

а) яка перевіряються за допомогою статистичних критеріїв;

б) на користь якої передбачається відхилити ;

в) яку передбачається прийняти;

г) яку передбачається відхилити.

6. Статистичний критерій це:

а) випадкова величина, закон розподілу якої відомий;

б) випадкова величина, закон розподілу якої невідомий;

в) випадкова величина, яка має нормальний закон розподілу;

г) випадкова величина, яка має закон розподілу .

7. Варіаційний ряд це:

а) таблиця значень випадкової величини з вказаними оцінками частот;

б) відсортована за зростанням вибірка;

в) різниця між максимальним і мінімальним значенням вибірки;

г) відсортована таблиця значень випадкової величини з вказаними оцінками частот;

д) відсортована за убуванням вибірка.

8. Гістограма є:

а) емпіричним законом розподілу;

б) оцінкою теоретичної функції розподілу похибки вимірювання;

в) оцінкою щільності розподілу похибки вимірювання;

г) оцінкою вибіркової функції розподілу похибки вимірювання;

д) оцінкою теоретичного закону розподілу похибки вимірювання.

9. Вибіркове математичне сподівання обчислюється за формулою:

а) ;

б) ;

в) ;

г) ;

д) .

10. Вибіркова виправлена дисперсія обчислюється за формулою:

а) ;

б);

в) ;

г) ;

д) .

11. Математичне сподівання є характеристикою:

а) середнього значення похибки вимірювання;

б) середньозваженого значення похибки вимірювання;

в) ступеню несиметрії розподілу;

г) ступенем плосковершиності розподілу похибки вимірювання;

д)степені розсіювання похибки вимірювання.

12. Дисперсія є характеристикою:

а) середнього значення похибки вимірювання;

б) середньозваженого значення похибки вимірювання;

в) ступеню несиметрії розподілу;

г) ступенем плосковершиності розподілу похибки вимірювання;

д) степені розсіювання похибки вимірювання.

13. Асиметрія є характеристикою:

а) середнього значення похибки вимірювання;

б) середньозваженого значення похибки вимірювання;

в) ступеню несиметрії розподілу;

г) ступенем плосковершиності розподілу похибки вимірювання;

д) степені розсіювання похибки вимірювання.

14. Ексцес є характеристикою:

а) середнього значення похибки вимірювання;

б) середньозваженого значення похибки вимірювання;

в) ступеню несиметрії розподілу;

г) ступенем плосковершиності розподілу похибки вимірювання;

д) степені розсіювання похибки вимірювання.

15.Медіана є характеристикою:

а) середнього значення похибки вимірювання;

б) середньозваженого значення похибки вимірювання;

в) ступеню несиметрії розподілу;

г) ступенем плосковершиності розподілу похибки вимірювання;

д)степені розсіювання похибки вимірювання.

16. Рівень надійності це:

а) ймовірність похибки другого роду;

б) гостована ймовірність гарантії даного статистичного висновку;

в) ймовірність похибки першого роду;

г) гостована ймовірність, яка гарантує, що дані статистичні висновки є правильними з надійністю;

д) гостована ймовірність, яка гарантує, що дані статистичні висновки є правильними з надійністю.

17. Ймовірність похибки першого роду це ймовірність:

а) відхилити правильну гіпотезу;

б) прийняти правильну;

в) відхилити неправильну;

г) прийняти неправильну.

18. Ймовірність похибки першого роду це ймовірність:

а) відхилити правильну гіпотезу;

б) прийняти правильну;

в) відхилити неправильну;

г) прийняти неправильну.

19. Нуль-гіпотеза відхиляється, якщо:

а) спостережуване значення статистичного критерію більше критичного;

б) спостережуване значення статистичного критерію менше критичного;

в) якщо ;

г) якщо .

20. Які математичні операції допускають результати вимірювань у номінальній шкалі:

а) ;

б);

в);

г);

д);

е)-;

ж)*;

з)/.

21. Які математичні операції допускають результати вимірювань у порядковій шкалі:

а) ;

б);

в);

г);

д);

е)-;

ж)*;

з)/.

22. Які математичні операції допускають результати вимірювань у інтервальній шкалі:

а) ;

б);

в);

г);

д);

е)-;

ж)*;

з)/.

23. Які математичні операції допускають результати вимірювань у відносній шкалі:

а) ;

б);

в);

г);

д);

е)-;

ж)*;

з)/.

24. Застосування яких оцінок є коректним до результатів вимірювань у номінальній шкалі:

а)частота;

б)відносна частота;

в)модальний клас;

г)мода;

д)медіана;

е)центілі;

ж)коефіцієнт рангової кореляції;

з)середнє арифметичне;

і)вибіркова дисперсія;

й)СКВ.

25. Застосування яких оцінок є коректним до результатів вимірювань у порядковій шкалі:

а)частота;

б)відносна частота;

в)модальний клас;

г)мода;

д)медіана;

е)центілі;

ж)коефіцієнт рангової кореляції;

з)середнє арифметичне;

і)вибіркова дисперсія;

й)СКВ.

26. Застосування яких оцінок є коректним до результатів вимірювань у інтервальній шкалі:

а)частота;

б)відносна частота;

в)модальний клас;

г)мода;

д)медіана;

е)центілі;

ж)коефіцієнт рангової кореляції;

з)середнє арифметичне;

і)вибіркова дисперсія;

й)СКВ.

27. Застосування яких оцінок є коректним до результатів вимірювань у відносній шкалі:

а)частота;

б)відносна частота;

в)модальний клас;

г)мода;

д)медіана;

е)центілі;

ж)коефіцієнт рангової кореляції;

з)середнє арифметичне;

і)вибіркова дисперсія;

й)СКВ.

28. На п’ятиквантильному графіку («Ящик з вусами») зображені оцінки наступних числових характеристик:

а) мода;

б)медіана;

в)середнє арифметичне;

г)коефіцієнт рангової кореляції;

д)середнє арифметичне;

е)вибіркова дисперсія;

ж)СКВ.

з) 5%-ий квантиль;

і) 95%-ий квантиль;

й) 25%-ий квантиль;

к) 75%-ий квантиль;

29. Перевірка однорідності дисперсій проводиться за критерієм:

а) Стьюдента;

б) Фішера;

в) Бартлетта;

г) Кохрена.

30. Задача однофакторного дисперсійного аналізу за Фішером полягає у перевірці наступної пари статистичних гіпотез:

а)

;

б)

;

в)

;

г)

;

д) .

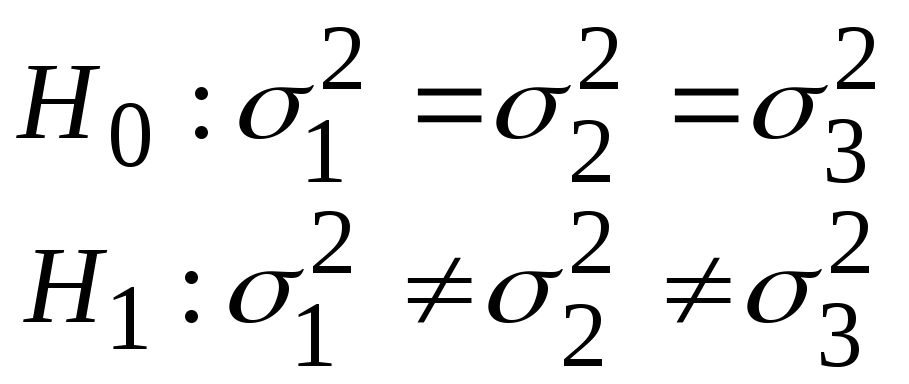31. Задано статистичний розподіл дискретної випадкової величини :

	0,5	1,5	2,5
	0,2	0,6	0,2

Вибіркове математичне сподівання в.в. дорівнює:

а) 1,2 б) 1,5 в) -0,5 г) 2 д) 1,8

32. Задано статистичний розподіл дискретної випадкової величини :

	0,5	1,5	2,5
	0,2	0,6	0,2

Вибіркова дисперсія в.в.дорівнює:

а) 3,2 б) 0,8 в) 0,4 г) 0,2 д) 1,0

33. Задано статистичний розподіл дискретної випадкової величини :

	0,5	1,5	2,5
	0,2	0,6	0,2

Оцінка ймовірності події дорівнює:

а) 0,2 б) 0,5 в) 0,8 г) 0,6 д)1

34. Задано статистичний розподіл дискретної випадкової величини :

	0,5	1,5	2,5
	0,2	0,6	0,2

Оцінка асиметрії розподілу в.в.дорівнює:

а) 0,6 б) -0,5 в) 0,1 г) -1 д) 0

35. Задано статистичний розподіл дискретної випадкової величини :

	0,5	1,5	2,5
	0,2	0,6	0,2

Оцінка ексцесу розподілу в.в. дорівнює:

а) 2,029 б) -2,029 в) 2,059 г) -1 д) -0,971

36. Точковою оцінкою параметра називається:

а) б) в) г) інтервал , що покриває оцінюваний параметр д) інтервал , що не покриває оцінюваний параметр .

37. Інтервальною оцінкою параметра нормального розподілу при відомому є:

а) , – об’єм вибірки, ,

б) , – об’єм вибірки, – квантиль розподілу Ст’юдента,

в) , – об’єм вибірки, ,

г) , – об’єм вибірки, – квантиль розподілу Ст’юдента,

д) , – об’єм вибірки, – квантиль розподілу Ст’юдента, – виправлена оцінка СКВ.

38. Інтервальною оцінкою параметра нормального розподілу при невідомому є:

а) , – об’єм вибірки, ,

б) , – об’єм вибірки, – квантиль розподілу Ст’юдента,

в) , – об’єм вибірки, ,

г) , – об’єм вибірки, – квантиль розподілу Ст’юдента,

д) , – об’єм вибірки, – квантиль розподілу Ст’юдента, – виправлена оцінка СКВ.

39. Інтервальною оцінкою математичного сподівання довільного розподілу є:

а) , – об’єм вибірки, ,

б) , – об’єм вибірки, – квантиль розподілу Ст’юдента,

в) , – об’єм вибірки, ,

г) , – об’єм вибірки, – квантиль розподілу Ст’юдента,

д) , – об’єм вибірки, – квантиль розподілу Ст’юдента, – виправлена оцінка СКВ,

е) , – об’єм вибірки, .

40. Параметри генератора псевдовипадкових чисел , що входить до інтегрованого середовища , за замовчанням дорівнюють , . Для даного випадку: (1 бал)

1. Математичне сподівання дорівнює:

а) 1 б) 0,5 в) 0,083 г) 0,289 д) 0

2. Дисперсія дорівнює:

а) 1 б) 0,5 в) 0,083 г) 0,289 д) 0

3. Середнє квадратичне відхилення дорівнює:

а) 1 б) 0,5 в) 0,083 г) 0,289 д) 0

4. Ймовірність того, що :

а) 1 б) 0,5 в) 0,083 г) 0,289 д) 0

41. Часовий інтервал між надходженнями пакетів даних у комп’ютерній мережі зі швидкістю передачі даних 10 Мбіт/сек підприємства має експоненціальний розподіл з параметром (1 бал).

1. Середня довжина інтервалу дорівнює:

а) 0,1 б) 0,007 в) г) 0,067 д)

2. Дисперсія довжини інтервалу дорівнює:

а) 0,1 б) 0,007 в) г) 0,067 д)

3. СКВ довжини інтервалу дорівнює:

а) 0,316 б) 0,084 в) 0,258 г) 0,067 д) 0,017

4. Ймовірність того, що часовий інтервал між надходженнями пакетів перевищить дорівнює:

а) 0 б) 0.1 в) 0.15 г) 0.25 д) 0.31

5. Ймовірність того, що часовий інтервал між надходженнями пакетів буде у межах 10<Х<15 мкс дорівнює:

а) 0 б) 0.1 в) 0.15 г) 0.25 д) 0.31

42. Відомо, що оцінка середньої кількості пакетів, яку генерує один з терміналів локальної мережі підприємства протягом години має нормальний розподіл з параметрами .

Ймовірність того, що за годину кількість пакетів відхилиться від середнього менше, ніж на дорівнює:

а) 0,383 б) в) г) д) 0,309

43. Відомо, що оцінка середньої кількості пакетів, яку генерує один з терміналів локальної мережі підприємства протягом години має нормальний розподіл з параметрами .

Ймовірність того, що за годину кількість пакетів буде від 9 до 11 дорівнює:

а) 0,383 б) в) г) д) 0,309

44. Відомо, що оцінка середньої кількості пакетів, яку генерує один з терміналів локальної мережі підприємства протягом години має нормальний розподіл з параметрами .