Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный государственный заочный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1_teoriya-i-metodyi-stat-prog-ya.pdf

Скачиваний:

215

Добавлен:

16.02.2016

Размер:

2.34 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 197 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

6. Вероятностные методы прогнозирования

Часто на практике приходится иметь дело с задачей прогнозирования случайных величин, и это является предпосылкой применения вероятностных моделей. Вероятностные модели позволяют вычислить вероятность того, что будущее значение параметра прогнозируемого процесса будет меньше определенного числа, например, вероятность того, что y < yi

Pi = P(y < yi ).

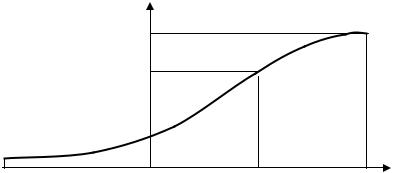
Величина y может находиться в пределах y0 ≤ y ≤ yn так, как в соответствии с рис. 6.1 P(y < y0 )= 0 и P(y < yn )=1

1,0

Рi

yn y

Рис. 6.1. Функция распределения вероятностей

Показанная на рисунке кривая распределения непрерывной случайной величины y является графиком функции распределения P(y). Функция распределения существует как для непрерывных, так и для дискретных случайных величин и является универсальной характеристикой случайных величин.

Зная функцию распределения, можно найти вероятность попадания случайной величины на заданный участок y0 ≤ y ≤ yn :

P(yi ≤ y ≤ yn )=1 − Pi .

Для непрерывных случайных величин очень часто рассматривается

производная функции распределения

f (y)= dPdy(y),

или плотность распределения непрерывной случайной величины y. Вероятность попадания случайной величины y на некоторый участок

P(y1 ≤ y ≤ y2 )= ∫ f (y)dy .

Таким образом, прогнозирование вероятности того или иного события может быть осуществлено при прогнозировании рассмотренных функций распределения. Причем во многих практических случаях нет необходимости характеризовать случайную величину полностью, а бывает достаточно спрогнозировать только некоторые параметры распределения (например, математическое ожидание и дисперсию).

В некоторых случаях полученные в результате наблюдений за прогнозируемым процессом данные могут быть описаны широкоизвестными распределениями непрерывных и дискретных случайных величин, среди которых: нормальное распределение, равномерное распределение, экспоненциальное распределение, распределение Пуассона и некоторые другие.

Если вид и параметры названных распределений не меняются по времени и в распоряжении имеется достаточное по объему количество наблюдений, то решение задачи прогнозирования не вызывает особых затруднений. Строится эмпирическое распределение, решается вопрос о выборе для данного эмпирического распределения теоретической кривой распределения и по ней с требуемой точностью производится прогнозирование. Однако на практике, как правило, в распоряжении исследователя имеется ограниченная информация о процессе и, кроме того, не всегда можно гарантировать неизменность вида и параметров распределения. Эти условия предопределяют применение более сложных вероятностных моделей, базирующихся на последних достижениях теории вероятностей. К таким наиболее интенсивно разрабатываемым областям

теории вероятностей относятся, в частности, теория малых выборок и теория суммирования случайного числа независимых случайных величин.

6.1. Приложение теории суммирования случайного числа независимых случайных величин в задачах прогнозирования

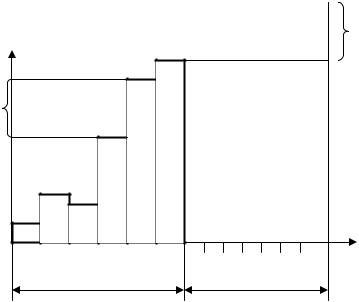
Постановка задачи. В результате анализа объекта прогнозирования и прогнозного фона на периоде ретроспекции (периоде основания прогноза) установлено, что процесс развития системы может быть представлен ступенчатым процессом (последовательностью скачков, совершаемых в случайные моменты времени). Величина скачка yi (рис. 6.2) является случайной величиной, поведение которой описывается законом распределения f (y). Число скачков n на периоде упреждения прогноза является случайным,

y
yi
	f (yn) = ?
Tоснов	1 2…	r…	t
	1 2…	r…
	Tупреж

Рис. 6.2. Постановка задачи

распределенным по закону Pn . Требуется определить функцию распределения выходного параметра системы y.

y1 , y2 ,..., yr ,..., yn

Решение. Традиционным (основным) аналитическим аппаратом теории вероятностей и математической статистики является аппарат характеристических функций. Известно, что если Y – действительная случайная величина, то существует комплексная случайная величина

X = exp{itY}(где i = −1 – мнимая единица, t – действительное число).

Функция вида

ϕ(t)= EX = EeitY ,

где E – символ математического ожидания, называется характеристической функцией случайной величины Y , то есть характеристическая функция случайной величины Y есть математическое ожидание комплексной случайной величины X .

Характеристическая функция безразмерна, а параметр t имеет размерность, обратную размерности случайной величины Y .

Используем основные свойства характеристических функций для решения задачи, из условия решения которой известно, что выходной параметр системы y зависит как от случайного числа скачков n на периоде упреждения,

так и от случайной величины yi каждого скачка. При этом случайные

величины независимы, одинаково распределены и не зависят

от случайной величины n.

Примем, что число скачков на периоде упреждения прогноза может быть определено законом Пуассона

P (r = n)= λne−λ ,

n = 0 ,1 ,2 ...

n n!

с параметром λ, причем для распределения Пуассона справедливо соотношение λ = n .

Случайная же величина y (величина скачка) имеет стандартное нормальное распределение N(0,1) с параметрами my = 0, σ 2 =1 и

	87
плотностью вероятности
f (y)=	1	e−	y2	.
f (y)=	1	e−	2	.
	2π

Таким образом, чтобы получить закон распределения выходного параметра, необходимо рассмотреть распределение суммы пуассоновского числа стандартных нормальных величин.

На основании мультипликативного свойства характеристической функции – характеристическая функция суммы независимых случайных величин равна произведению характеристических функций случайных величин,

то есть если y = ∑yi , то

i =1

ϕ(t)= Eeity = ∏ϕi (t),

i=1

можно записать, что интегральная функция распределения F(y) суммы

случайного числа n случайных величин yi определяется характеристической функцией

∞

ϕ(t)= ∑Pnϕin (t),

n=0(1)

где ϕi (t) – характеристическая функция случайной величины yi .

Рассмотрим характеристическую функцию стандартного нормального распределения:

∞

y 2

∞

(y −it )2

t 2

ϕi (t)= ∫ eity

e −

dy =

∫e

−

dy =

−∞

2π

−∞

=e −

t 2

∞

−

(y −it )2

∫e

dy.

2π

−∞

∞

−

y 2

2π , то ϕ(t)= e−

t 2

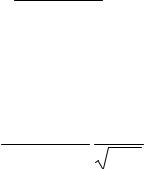
Так как интеграл ∫e

dy =

2 .

−∞

Отсюда характеристическая функция суммы пуассоновского числа стандартных нормальных величин имеет вид

∞	n	−λ		t 2		∞	n		t 2
ϕ(t)= ∑	λ e		e−		n =	∑	λ	e−λ−		n .
				2					2
n=0(1)	n!					n=0(1) n!

Для определенности случай n = 0 из рассмотрения исключим. Тогда

∞

t 2

ϕ(t)= ∑

e−λ−

n .

(1−e

−λ

)

n=1 n!

Исходя из формулы обращения

f (y)=

dF(y)

;

∞

f (y)

e−ity

∑Pnϕin (t),

2π −∞∫

n=1

тогда

∞

n −λ

∞

f (y)=

∑n=1

λ(1 −e e−λ )−∫∞e−ity−

ndt .

2π

В результате интегрирования получим искомую плотность распределения:

∞	n	−λ					y2
f (y)= ∑	λ e				1	e−
			−λ	)			2n .
n=1	n! (1 − e				2πn

В табл.6.1. приведем формулы для характеристических функций, наиболее часто встречающихся при решении практических задач.

Решим поставленную задачу при условии, что величина скачка yi

равномерно распределена на интервале (− a,a). Такое допущение о законе распределения скачка представляется целесообразным для коротких динамических рядов. Симметричность интервала не снижает общности рассуждений.

f (y)

Характеристическая функция для функции распределения суммы случайного числа случайных величин yi , распределенных равномерно на интервале (− a,a),

ϕ(t)= ∑∞ Pn sinn (ta).

n=1 (ta)n

Таблица 6.1. Характеристические функции

Распределение

Плотность распределения

Равномерное					1		y	(0,a)
Равномерное					a ,
					a ,
Равномерное				1			y (− a,a)
Равномерное				2a ,
				2a ,
Показательное			λe−λy ,					y (0,∞)
Гамма		λ(λy)n−1 e−λy
									, y (0,∞)
			Γ (n)
			Γ (n)
	1				−	(y −m)2
Нормальное	1				−		2σ 2	, y (−∞,∞)
	σ 2π e							, y (−∞,∞)

Характеристическая

функция

eiat −1

iat sin at

(1−itλ−1 )−1 (1−itλ−1 )−n

itm−t 2 σ 3

e 2

В соответствии с формулой обращения запишем формулу для плотности распределения:

f (y)=	1	∞	∞	sin	n	(ta	)
		e−ity ∑Pn						dt .
	2π					n
		−∫∞	n=1	(ta)

Изменяя порядок суммирования и интегрирования и учитывая, что симметричные законы распределения в характеристической функции не имеют членов, содержащих мнимую единицу, плотность распределения представим в виде

	1	∞	∞	n	)
f (y)=		∑n=1 Pn ∫0		sin (ta		costy dt .
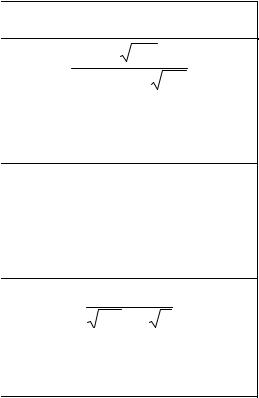
	π			(ta)n

Используя табличный интеграл вида

∞ sin y		4
		cos my dy ,

∫0	y

находим плотность распределения выходной величины:

n−1

∞

(−1) n +

−

f (y)=

∑Pn

∑

k! (n −k )!

a n=1

0<k <g

n +

при 0 <

< n ,

где g =

f (y)−0 ,

при

n ≥

≥ 2.

В табл. 6.2 приведены выражения для плотностей распределения выходной координаты при других условиях решениях поставленной задачи.

Таблица 6.2. Расчетные соотношения для плотности распределения

величины Y

Закон распределения

Плотность распределения

f (y)

числа скачков n

величины скачка y

λn

nσ

2π ×

Пуассона, параметр λ

Нормальный,

∑n! (1−e−λ )

m,σ

параметры

(y −mn)

+λ

×exp −

λn µ(µx)n−1

Экспоненциальный,

∞

e−λ

−µx

То же

параметр µ

∑n=1

1−e−λ

Γ (n)

∞

e−λ

λn k(kx)mn−1

Гамма-,

−kx

То же

параметры m, k

∑n=1

1 − e−λ

Γ (mn)

∞

−λ

∑

То же

Логнормальный, параметры

n=1

2πσn!

m,σ 2

[ln y −ln(mn)]2

×exp −

Окончание табл. 6.2

То же

Равномерный [–a, a]

	Биномиальный, параметр	Нормальный,
	Биномиальный, параметр	параметры m,σ 2
	р	параметры m,σ 2

	То же	Экспоненциальный,
	То же	параметр µ
		параметр µ
	То же	Гамма-,
	То же	параметры m, k
		параметры m, k

	∞			−	λ
	∑n e				n	×
	n=1	an!2
	k				y			n−1
	(−1)	n +				− 2k
	(−1)	n +			a	− 2k
×∑					a
×∑		k! (n − k )!
k		k! (n − k )!
							y
			n		+
			n		+
	0 < k <						a
	0 < k <				2
					2

∞

∑ nσ Cnk pk (1− p)n−k × n=1

×exp − (y −mn)2

∞	n−1			−µy
∑Cnk pk (1− p)n−k µ(µy)		e
n=1	Γ (n)
∞	mn−1		e		−ky
∑Cnk pk (1− p)n−k	k(ky)
	Γ (mn)
n=1

Необходимо помнить, что если Eyi < ∞ и En < ∞, а zn = y1 + y2 + + ...+ yn , то для математического ожидания суммы случайного числа случайных слагаемых справедлива так называемая формула Вальда

Ezn = Eyi En .

Дисперсия суммы может быть определена через второй момент:

Ezn2 = En[Eyi2 −(Eyi )2 ] + En2 (Eyi )2 ,

откуда

Dzn = En[Eyi2 −(Eyi )2 ] + (Eyi )2[En2 −(En )2 ].

Рассмотрим еще один подход, при котором теоретическая вероятностная модель сочетается с экстраполяционной моделью на ЭВМ. Этот подход применяется тогда, когда вероятностную модель трудно составить из-за больших неопределенностей или модель трудно исследовать из-за ее

yi −1

сложности. При использовании этого метода, неопределенности «реализуются» случайным образом, путем использования процедуры Монте-Карло.

6.2. Ориентированный процесс случайного блуждания как метод вероятностного моделирования

В основу данного метода положен подход, не связанный с использованием жесткой структуры модели и серьезными требованиями к объему априорной информации. Сущность метода заключается в представлении используемого для прогнозирования динамического ряда в качестве определенным образом ориентированного процесса случайного блуждания.

Значение изменяющегося параметра объекта прогнозирования для каждого момента на периоде ретроспекции можно представить в виде

yi = yi −1 + ei −1 (i =1,...,N ),

где yi – значение динамического ряда в i-й момент времени (год) периода ретроспекции;

– значение динамического ряда в предыдущий момент времени; ei −1 – приращение переменной объекта прогнозирования в i-й момент

времени по сравнению с предыдущими;

N – число значений динамического ряда.

Поскольку приращения носят случайный характер, для них можно определить вид закона распределения и его параметры. При этом нужно учесть характер зависимости последующих приращений от предыдущих.

Предполагается, что в период упреждения характер изменений динамического ряда сохраняется. Тогда, используя характеристики приращений, метод статистических испытаний можно применить для моделирования приращений в период упреждения прогноза.

Значение единичной реализации прогноза на каждом последующем шаге

прогнозирования будет

x j = x j −1 +ei (i =1,...,M ),

где j – номер шага на периоде упреждения;

M – число шагов на периоде упреждения;

xj-1– значение переменной объекта прогнозирования на предыдущем

шаге;

ej – моделируемое значение приращения на j-м шаге. Производя данную процедуру до момента упреждения, получаем

значение точечного прогноза:

xпр = yN + ∑eˆj ,

j =1

где xпр – точечный прогноз на М-й период упреждения; yN – конечное значение динамического ряда.

При разыгрывании данной процедуры многократно образуется совокупность случайных значений точечного прогноза. По полученной выборке значений xпр определяется среднее значение прогноза и его дисперсия:

			k	M
xпр = yN	+	1 ∑∑ejk			;	(6.1)
		k k =1 j =1
σпр2	=	1		∑k (xпр k − xпр )2 ,		(6.2)
σпр2	=			∑k (xпр k − xпр )2 ,		(6.2)
			k −1 k =1

где k – число реализаций точечного прогноза;

ejk – разыгрываемое значение приращения на j-м шаге периода упреждения в k-й реализации точечного прогноза;

xпр k – значение k-й реализации точечного прогноза, определяемое по зависимости (6.1).

Таким образом, процедура прогнозирования сводится к многократной имитации приращений на периоде упреждения и к последующему определению

статистических характеристик (среднего и дисперсии) реализаций точечного прогноза.

При наличии репрезентативной выборки приращений моделирование можно осуществить в соответствии с определенным по этой выборке эмпирическим законом распределения приращений.

Для коротких динамических рядов можно применить допущение о нормальности отклонений значений динамического ряда от тренда. При этом допущении плотность распределения приращений также является нормальной. При наличии на периоде ретроспекции малого объема (короткие

динамические ряды) для моделирования приращений целесообразно использовать двумерное нормальное распределение. Двумерная плотность вероятности зависит от пяти параметров:

−

−e

−

f (e

exp

)

2πσ −

σ +

− r2

−

2(1− r2 )

σ−2

−

−e

)(e

−e

)

−e

)

− 2r

−

+ 2

σ σ

σ 2

−

где e− ,e+ ,e − ,e + ,σ− ,σ+ – случайные значения, математические ожидания и среднеквадратические отклонения предыдущих и последующих приращений переменной прогнозирования соответственно;

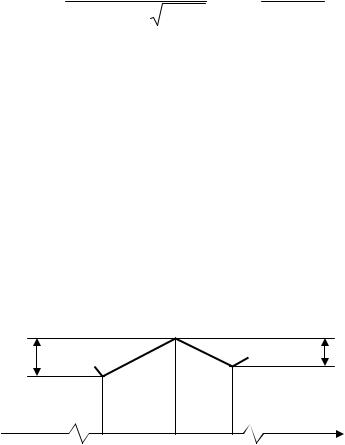
r – коэффициент корреляции последующих приращений на предыдущие. Графически определение предыдущих и последующих приращений

показано на рис. 6.3.

e−		ei+
i
yi −1	y	yi +1
		t

Рис. 6.3. Определение предыдущих и последующих приращений

Очевидно, что одно и то же приращение в зависимости от того, относительно какой точки оно рассматривается, может быть как предыдущим, так и последующим. Однако первое приращение является только предыдущим.

При обработке исходного динамического ряда определяются оценки математических ожиданий и дисперсий предыдущих и последующих

приращений. Множество предыдущих приращений ε− = {e−}определяется по
					i
зависимости
e− = y − y			, i =
e− = y − y		i −1	, i =	1,N −1.
i	i	i −1

Множество последующих приращений ε+ = {ei+}определяется по зависимости

= y

− y ,

i =1,N −2

или

e+ = e−

i+1

По множеству ε−определяются значения e − и оценка дисперсии σ−2

предыдущих приращений:

−

N −1

−

∑ei

;

N −1 i=1

N −1

−

∑

(ei

−e

) .

N − 2 i=1

Соответственно по множеству ε+ определяются значения e + и оценка

дисперсии σ +2 последующих приращений:

N −2

∑ei

;

N − 2

i =1

N −2

σ+

∑

(ei

−e

) .

N −3 i =1

Оценка значения коэффициента корреляции r определяется по зависимости

	1	N −2	(e− −e − )(e+ −e + )
r =		∑	i	i	.
r =	N − 4	∑		σ σ	.
		i =1		− +

Для моделирования случайных приращений на периоде упреждения используется алгоритм моделирования двумерного распределения. Для рассматриваемого случая моделирующая зависимость последующих

приращений e+jk

имеет вид

(α jk −0,5)1

r2 (e−jk −e − )2

ejk = e

σ+

2π

1− r

exp

2(1

− r2 )σ−2

−

(α jk −0,5)2 σ+

−

2 (e−jk −e − )2

(α jk −0,5)3

−

(ejk −e

)r2π exp

(1− r2 )σ−2

σ+ ×

σ−

−

3 r

−

−e

−

(ejk −e

)

(ejk

)

×(

2π )

−1

σ−2

(1− r2 )σ−2

+ ...

1− r

− r2

exp

При моделировании случайного значения e+jk

на первом шаге в каждой

k-й реализации e+	предыдущее значение e−			равно значению последнего
1k		1k
приращения на периоде основания eN−		−1 , то есть
	e−	= e−	.
	1k	N −1

При моделировании приращений на следующих шагах периода упреждения

e− = e+− . jk j 1,k

Оценка коэффициента корреляции, определяемая по выборкам малых объемов, является случайной.

Плотность вероятности выборочного коэффициента корреляции имеет сложный вид. При принятом допущении о нормальности распределения приращений используется нормализующее преобразование Фишера.

Случайная величина z распределена нормально с параметрами

					97
z =	1	ln	1+ r	;	σz2 =	1	,
z =	2	ln	1− r	;	σz2 =	N −5	,
	2		1− r			N −5

где r – значение выборочного коэффициента корреляции. Моделируем значение z как нормально распределенную случайную

величину по зависимости

z jk = z + v jkσz ,

где v jk – нормированная нормально распределенная случайная величина,

моделируемая с помощью алгоритма.

Осуществляя обратный по отношению к преобразованию Фишера переход, получим случайное значение коэффициента корреляции:

e2z −1

rjk = e2jkz +1 jk

С учетом изложенного моделирование приращений на периоде упреждения включает выполнение следующих действий:

1.Обращение к датчику нормированных нормально распределенных случайных чисел и получение v jk ;

2.Вычисление случайного значения rjk ;

3.Обращение к датчику равномерно распределенных случайных величин

иполучение числа α jk ;

4.Вычисление приращения e+jk при полученном значении rjk и α jk ;

5.Многократная имитация приращения и вычисление характеристик прогноза.

<<< < Предыдущая 1 2 3 4 5 67 / 197 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.02.20161.71 Mб321_matematika-ch--1,-2-y-semestr-2009-11-09.pdf
#
16.02.2016366.65 Кб101_praktika-doc.pdf
#
16.02.20161.27 Mб1781_sbornik-kontrolnih-rabot-po-fizike.pdf
#
16.02.20161.09 Mб261_sotsiologiya-svodnyiy-fayl-2010-03-22.pdf
#
16.02.20162.53 Mб241_tekctumk.pdf
#
16.02.20162.34 Mб2151_teoriya-i-metodyi-stat-prog-ya.pdf
#
16.02.20163.12 Mб921_toe-3-2009-12-22.pdf
#
16.02.2016944.68 Кб511_umk-2-,2-chast-2010-05-13.pdf
#
16.02.20161.25 Mб111_umk-finansyi-rio-ispr-2009-11-18.pdf
#
16.02.20161.89 Mб801_umk-perehodnyie-protsessyi.pdf
#
17.08.2019547.78 Кб82 курс. 2 полугодие. Правоведение. - Основы Пра...docx