72

9 5. Метод экспоненциального сглаживания. Выбор постоянной сглаживания

При использовании метода наименьших квадратов для определения прогнозной тенденции (тренда) заранее предполагают, что все ретроспективные данные (наблюдения) обладают одинаковой информативностью. Очевидно, логичнее было бы учесть процесс дисконтирования исходной информации, то есть неравноценность этих данных для разработки прогноза. Это достигается в методе экспоненциального сглаживания путем придания последним наблюдения динамического ряда (то есть значениям, непосредственно предшествующим периоду упреждения прогноза) более значимых «весов» по сравнению с начальными наблюдениями. К достоинствам метода экспоненциального сглаживания следует также отнести простоту вычислительных операций и гибкость описания различных динамик процесса. Наибольшее применения метод нашел для реализации среднесрочных прогнозов [2].

5.1. Сущность метода экспоненциального сглаживания

Сущность метода состоит в том, что динамический ряд сглаживается с помощью взвешенной «скользящей средней», в которой веса подчиняются экспоненциальному закону. Другими словами, чем дальше от конца временного ряда отстоит точка, для которой вычисляется взвешенная скользящая средняя, тем меньше «участия она принимает» в разработке прогноза.

Пусть исходный динамический ряд состоит из уровней (составляющих ряда) yt , t =1,2,...,n . Для каждых m последовательных уровней этого ряда

(m<n) можно подсчитать среднюю величину. Вычислив значение средней для первых m уровней y1 , y2 ,..., ym , переходят затем к расчету средней для уровней y2 , y3 ,..., ym+1 и так далее. Таким образом, интервал сглаживания, то есть интервал, для которого подсчитывается средняя, как бы скользит по

73

динамическому ряду с шагом, равным единице. Если m – нечетное число, а предпочтительно брать нечетное число уровней, поскольку в этом случае расчетное значение уровня окажется в центре интервала сглаживания и им легко заменить фактическое значение, то для определения скользящей средней можно записать следующую формулу:

где yt – значение скользящей средней для момента t (t =1,2,...,n); yi – фактическое значение уровня в момент i ;

i – порядковый номер уровня в интервале сглаживания.

Величина ξ определяется из продолжительности интервала сглаживания.

Поскольку

m = 2ξ +1

при нечетном m , то

ξ = m2−1.

Расчет скользящей средней при большом числе уровней можно упростить, определяя последовательные значения скользящей средней рекурсивно:

Но исходя из того, что последним наблюдениям необходимо придать больший «вес», скользящее среднее нуждается в ином толковании. Оно заключается в том, что полученная с помощью усреднения величина заменяет не центральный член интервала усреднения, а его последний член. Соответственно этому последнее выражение можно переписать в виде

74

Здесь скользящая средняя, относимая к концу интервала, обозначена новым символом M i . По существу, M i равно yt , сдвинутому на ξ шагов вправо, то есть M i = yt +ξ , где i = t +ξ .

Учитывая, что M i−1 является оценкой величины yi−m , выражение (5.1)

можно переписать в виде

Вычисления, проводимые по выражению (5.3) с каждым новым наблюдением, называются экспоненциальным сглаживанием. В последнем выражении для отличия экспоненциального сглаживания от скользящего среднего введено обозначение Q вместо M . Величина α , являющаяся

аналогом m1 , называется постоянной сглаживания. Значения α лежат в

интервале [0,1]. Если α представить в виде ряда

α +α(1 −α)+α(1 −α)2 +α(1 −α)3 + ...+α(1 −α)n ,

то нетрудно заметить, что «веса» убывают по экспоненциальному закону во времени. Например, для α = 0,2 получим

0,2 + 0,16 + 0,128 + 0,102 + 0,082 + …

Сумма ряда стремится к единице, а члены суммы убывают со временем.

Величина Qt в выражении (5.3) представляет собой экспоненциальную среднюю первого порядка, то есть среднюю, полученную непосредственно при

75

сглаживании данных наблюдения (первичное сглаживание). Иногда при разработке статистических моделей полезно прибегнуть к расчету экспоненциальных средних более высоких порядков, то есть средних, получаемых путем многократного экспоненциального сглаживания.

Общая запись в рекуррентной форме экспоненциальной средней порядка k имеет вид

Q t( k ) = αQ t( k −1 ) + (1 − α )Q t(−k1 ) .

Величина k изменяется в пределах 1, 2, …, p, p+1, где p – порядок прогнозного полинома (линейного, квадратичного и так далее).

На основе этой формулы для экспоненциальной средней первого, второго и третьего порядков получены выражения

Qt(1) = αyt + (1 − α )Qt(−11) ;

Qt(2 ) = αQt(1) + (1 − α )Qt(−21); Qt(3 ) = αQt(2 ) + (1 − α )Qt(−31) .

5.2. Определение параметров прогнозной модели методом экспоненциального сглаживания

Очевидно, что для разработки прогнозных значений на основе динамического ряда методом экспоненциального сглаживания необходимо вычислить коэффициенты уравнения тренда через экспоненциальные средние. Оценки коэффициентов определяются по фундаментальной теореме БраунаМейера, связывающей коэффициенты прогнозирующего полинома с экспоненциальными средними соответствующих порядков:

где aˆ p – оценки коэффициентов полинома степени р.

Коэффициенты находятся решением системы ( p +1) уравнений с p +1

неизвестными.

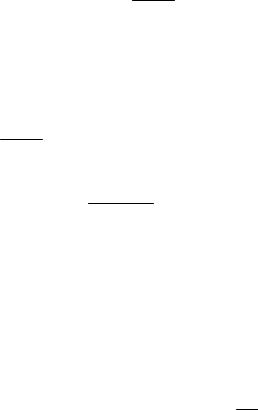
76

Так, для линейной модели

aˆ0 = 2Qt(1) −Qt(2); aˆ1 = 1 −αα (Qt(1) −Qt(2));

для квадратичной модели

aˆ0 = 3(Qt(1) −Qt(2))+ Qt(3);

aˆ1 = 1 −αα [(6 −5α)Qt(1) − 2(5 − 4α)Qt(2) + (4 −3α)Qt(3)];

aˆ 2 = (1 −αα)2 [Qt(1) − 2Qt(2) + Qt(3)].

Прогноз реализуется по выбранному многочлену соответственно для линейной модели

ˆyt+τ = aˆ 0 + aˆ1τ ;

для квадратичной модели

ˆyt+τ = aˆ0 + aˆ1τ + aˆ22 τ 2 ,

где τ – шаг прогнозирования.

Необходимо отметить, что экспоненциальные средние Qt(k ) можно вычислить только при известном (выбранном) параметре, зная начальные условия Q0(k ).

Оценки начальных условий, в частности, для линейной модели

77

для квадратичной модели

где коэффициенты a0 и a1 вычисляются методом наименьших квадратов.

Величина параметра сглаживания α приближенно вычисляется по формуле

α ≈ m2+1 ,

где m – число наблюдений (значений) в интервале сглаживания. Последовательность вычисления прогнозных значений представлена на

рис. 5.1.

В качестве примера рассмотрим процедуру получения прогнозного значения безотказной работы изделия, выражаемой наработкой на отказ.

Исходные данные сведены в табл. 5.1.

78

Выбираем линейную модель прогнозирования в виде yt = a0 + a1τ

Решение осуществим со следующими значениями начальных величин:

a0,0 = 64,2 ; a1,0 = 31,5 ; α = 0,305.

Таблица 5.1. Исходные данные

«Сглаженная» величина y2 при этом вычисляется по формуле

ˆy2 = a0,1 + a1,1τ = 97,9 +31,9 1 =129,8.

Результаты дальнейших вычислений сведены в табл. 5.2.

79

Таблица 5.2. Результаты вычислений ˆyt

Таким образом (табл. 5.2), линейная прогнозная модель имеет вид

ˆyt +τ = 224,5 + 32τ .

Вычислим прогнозные значения для периодов упреждения в 2 года (τ =1), 4 года (τ = 2) и так далее наработки на отказ изделия (табл. 5.3).

Таблица 5.3. Прогнозные значения ˆyt

Следует отметить, что суммарный «вес» последних m значений временного ряда можно вычислить по формуле

c =1 − (m( −1)m) . m +1

Так, для двух последних наблюдений ряда ( m = 2) величина c =1 − (22−+11)2 = 0,667 .

80

5.3. Выбор начальных условий и определение постоянной сглаживания

Как следует из выражения

Qt =αyt + (1 −α)Qt−1,

при проведении экспоненциального сглаживания необходимо знать начальное (предыдущее) значение сглаживаемой функции. В некоторых случаях за начальное значение можно взять первое наблюдение, чаще начальные условия определяются согласно выражениям (5.4) и (5.5). При этом величины a0,0 , a1,0

и a2,0 определяются методом наименьших квадратов.

Если мы не очень доверяем выбранному начальному значению, то, взяв большое значение постоянной сглаживания α через k наблюдений, мы доведем

«вес» начального значения до величины (1 −α)k <<α , и оно будет практически забыто. Наоборот, если мы уверены в правильности выбранного начального значения и неизменности модели в течение определенного отрезка времени в будущем, α может быть выбрано малым (близким к 0).

Таким образом, выбор постоянной сглаживания (или числа наблюдений в движущейся средней) предполагает принятие компромиссного решения. Обычно, как показывает практика, величина постоянной сглаживания лежит в пределах от 0,01 до 0,3.

Известно несколько переходов, позволяющих найти приближенную оценку α . Первый вытекает из условия равенства скользящей и экспоненциальной средней

α = m2+1 ,

где m – число наблюдений в интервале сглаживания. Остальные подходы связываются с точностью прогноза.

Так, возможно определение α исходя из соотношения Мейера:

81

α ≈ S y ,

S1

где S y – среднеквадратическая ошибка модели;

S1 – среднеквадратическая ошибка исходного ряда.

Однако использование последнего соотношения затруднено тем, что достоверно определить S y и S1 из исходной информации весьма сложно.

Часто параметр сглаживания, а заодно и коэффициенты a0,0 и a0,1

подбирают оптимальными в зависимости от критерия

S 2=α∑∞ (1 −α)j [yij − ˆyij ]2 → min

j=0

путем решения алгебраической системы уравнений, которую получают, приравнивая к нулю производные

Так, для линейной модели прогнозирования исходный критерий равен

S 2 =α∑∞ (1 −α)j [yij − a0,0 − a1,0τ]2 → min .

j=0

Решение этой системы с помощью ЭВМ не представляет никаких сложностей.

Для обоснованного выбора α также можно использовать процедуру обобщенного сглаживания, которая позволяет получить следующие соотношения, связывающие дисперсию прогноза и параметр сглаживания для линейной модели:

Sп2 ≈ [1 +αβ]2 [1 + 4β + 5β 2 + 2α(1 + 3β)τ + 2α2τ 3 ]S y2

для квадратичной модели

Sп2 ≈ [2α +3α3 +3α2τ]S y2 ,

82

где β =1 −α ; S y – СКО аппроксимации исходного динамического ряда.