335 13. Как найти положение опасного сечения вала при изгибе с

кручением?

14. Как записывается выражение для эквивалентного момента при изгибе с кручением вала круглого или кольцевого поперечного сечения в соответствии с третьей и четвертой гипотезами прочности?

15.Какой элемент конструкции называется оболочкой?

16.Что называется срединной поверхностью?

17.Что представляет собой тонкостенная осесимметричная оболочка?

18.В чем состоит расчет оболочки по безмоментной теории?

19.Какое сечение оболочки называется меридиональным?

20.Какое напряжение называется меридиональным?

21.Какое напряжение называется окружным?

22.Приведите уравнение Лапласа.

23.Какой цилиндр называется толстостенным?

24.Какие точки толстостенного цилиндра являются опасными?

Раздел 8. Устойчивость сжатых стержней Раздел 8 курса включает 6 тем: «Основные понятия», «Формула Эйлера

для критической силы», «Потеря устойчивости за пределом пропорциональности», «График зависимости критического напряжения от гибкости стержня», «Рациональные формы поперечного сечения» и

«Продольно-поперечный изгиб». После изучения раздела Вам следует ответить на вопросы для самопроверки.

Работа с разделом 8 завершается выполнением задачи №13 контрольной работы №3, выполнением лабораторной работы №8 согласно “Методическим

указаниям к выполнению лабораторных работ” и сдачей контрольного теста №8.

Для того, чтобы Вы смогли успешно ответить на вопросы контрольного теста, Вам предоставляется возможность поработать с репетиционным тестом.

336

Он является полным аналогом контрольного теста, однако время работы с ним неограничено, и на вопросы теста даются правильные ответы.

Если Вы испытываете затруднения при ответе на какой – либо вопрос, обратитесь к глоссарию или учебному пособию по сопротивлению материалов [ 3 ], раздел 3 “ Устойчивость центрально сжатых стержней”.

8.1. Основные понятия

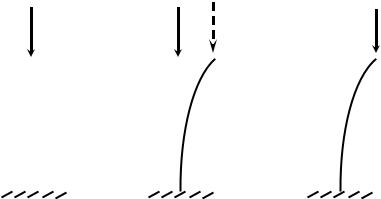
Центрально сжатые стержни помимо расчета на прочность необходимо рассчитывать на устойчивость (продольный изгиб). При потере устойчивости ось стержня изгибается и стержень испытывает совместное действие сжатия с изгибом (рис. 8.1).

Наименьшее значение сжимающей силы, при котором сжатый стержень теряет способность сохранять прямолинейную форму равновесия, называется критической силой и обозначается Pкр.

Рис.8.1.

Даже при незначительном превышении критического значения нагрузки возникают недопустимо большие прогибы и напряжения, поэтому состояние

стержня, соответствующее критической силе следует считать опасным

(предельным).

Для обеспечения определенного запаса устойчивости необходимо, чтобы удовлетворялось условие:

P ≤ [P],

337

где [P] – допускаемая нагрузка, [P] = [PКР] ;

п у

[п]у – требуемый коэффициент запаса устойчивости.

8.2. Формула Эйлера для критической силы

Критическая сила Ркр (при потере устойчивости в упругой стадии)

вычисляется по формуле Эйлера:

сечения; µ - так называемый коэффициент приведения длины, зависящий от способа закрепления концов стержня.

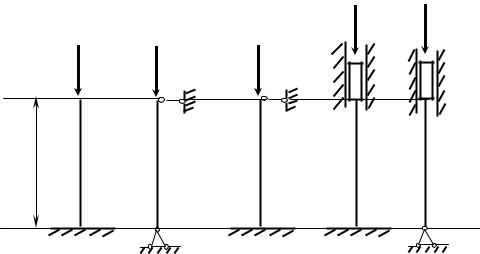
На рис.8.2 показано несколько видов закрепления стержня и указаны

соответствующие значения коэффициента μ приведения длины.

l

Рис. 8.2

Напряжение, возникающее в поперечном сечении стержня при достижении

сжимающей силой критического значения, называется критическим

напряжением σкр .Формула Эйлера справедлива при условии σкр ≤ σпц

(критическое напряжение не превышает предела пропорциональности). Обычно условие применимости формулы Эйлера выражают через гибкость стержня λ,

338

поперечного сечения).

Условие применимости формулы Эйлера в этом случае имеет вид:

λ ≥ λпред ,

где λпред – предельная гибкость стержня, зависящая от физико-механических

8.3. Потеря устойчивости за пределом пропорциональности

Явление потери устойчивости имеет место и для стержней, гибкость которых меньше предельной λ < λпред. В этом случае формула Эйлера

неприменима, т.к. критическое напряжение, соответствующее критической силе Ркр , превышает предел пропорциональности: σкр > σпц .

формуле (8.2), становится равным пределу текучести σТ – напряжению, которое является опасным (предельным) при статическом нагружении.

8.4. График зависимости критического напряжения от гибкости стержня

Таким образом, сжатые стержни можно отнести к трем категориям:

1. стержни большой гибкости (λ ≥ λ пред), для которых справедлива формула Эйлера;

339 2. стержни средней гибкости (λ 0 < λ < λ пред), которая рассчитывается по

формуле Тетмайера – Ясинского; 3. стержни малой гибкости (λ ≤ λ 0), которые следует рассчитывать не на

устойчивость, а на прочность.

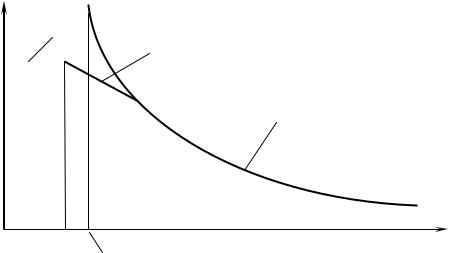
На рис. 8.3 приведён график зависимости σкр = σкр (λ) .

Из графика (рис. 8.3) видно насколько завышенным может оказаться значение критического напряжения, если для стержня средней гибкости (λ 0 < λ < λ пред) воспользоваться формулой Эйлера (см. пунктирную линию).

(λ0< λ< λпред))

Рис. 8.3

8.5. Рациональные формы поперечных сечений

При выборе формы поперечного сечения следует иметь в виду, что в

соответствии с формулой Эйлера (8.1) сечение тем выгоднее, чем больше его

минимальный момент инерции Jmin . При одной и той же площади А увеличение момента инерции сечения достигается сосредоточением материала

на периферии поперечного сечения. При этом необходимо стремиться к равенству главных центральных моментов инерции. Тогда при одинаковом

340

закреплении в главных плоскостях будет обеспечена равноустойчивость стержня.

Теоретически наиболее рациональным является кольцевое сечение, имеющее наибольший момент инерции при данной площади и одинаковую жесткость по всем направлениям. Также возможными являются коробчатые тонкостенные сечения и сечения, составленные из прокатных профилей,

раздвинутых на необходимое расстояние.

Наименее рациональны прямоугольные сплошные сечения. Примеры расчета стержня на устойчивость смотри в [ 3 ], раздел 3.

8.6. Продольно - поперечный изгиб

На рис. 8.4 представлена балка с шарнирно закрепленными концами, нагруженная некоторой поперечной силой Р и сжимающей силой S, действующей вдоль оси балки.

P

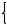
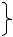y0 y

x

y

Рис. 8.4

В этом случае возникает продольно-поперечный изгиб - сочетание поперечного изгиба со сжатием или растяжением.

Полный прогиб y можно рассматривать состоящим из прогиба y0, возникающего от действия только поперечной нагрузки, и дополнительного прогиба, равного y – y0, вызванного силой S.

Для достаточно жесткой балки, для которой полный прогиб мало

отличается от прогиба y0, вызванного только поперечной силой, можно

пренебречь влиянием силы S и проводить ее расчет на совместное действие центрального сжатия и поперечного изгиба.

Для балки, жесткость которой невелика, влияние силы S на изгибающий момент и прогибы может быть существенным и пренебрегать им нельзя. В этом случае балку следует рассчитывать на продольно-поперечный изгиб.

341

Используя методику приближенного расчета, считаем, что дополнительный прогиб y – y0 принимает форму синусоиды

После подстановки этого соотношения в приближенное дифференциальное уравнение упругой линии можно получить выражение для прогиба балки при совместном действии продольной и поперечной

нагрузок:

Оно дает удовлетворительные результаты, когда сжимающая сила S не превосходит 0,8PЭ . В этом выражении PЭ – так называемая эйлерова сила,

вычисляемая по формуле π2 EJ , которая в отличие от критической силы Ркр l2

используется независимо от гибкости балки. При других типах опорных закреплений балки в формулу для вычисления эйлеровой силы РЭ вместо длины l балки следует подставлять приведенную длину (μl) .

В формулу для определения эйлеровой силы РЭ входит момент инерции относительно той из главных осей инерции поперечного сечения, которая

перпендикулярна плоскости действия поперечной нагрузки.

Наибольшие и наименьшие нормальные напряжения в поперечном

сечении при продольно-поперечном изгибе определяются по формуле:

σ= S ± M = S ± M 0 ± Sy . A W A W W

Кроме расчета на продольно-поперечный изгиб сжатоизогнутые стержни необходимо рассчитывать и на устойчивость, так как, например, продольно –

поперечный изгиб балки может происходить в вертикальной плоскости, а

потеря устойчивости – в горизонтальной плоскости.

Вопросы для самопроверки

1.В чем заключается явление потери устойчивости сжатого стержня?

2.Какая сила называется критической?

3.Напишите формулу Эйлера для определения критической силы. 4.Что называется гибкостью стержня? Какова ее размерность?

5.Чему равен коэффициент приведения длины для различных случаев закрепления концов стержня?

6.Что называется предельной гибкостью? Какова ее размерность?