Теория литейных процессов том1

141

Таблица 3.10

Потери напора ξсеч в зависимости от соотношения

площадей сечения элементов канала

3. Вход из широкой полости в узкий канал ξк. Этот вид сопротивления в литниковой системе проявляется при переходе от литниковой чаши или воронки к стояку. Если кромки не имеют скругления, то ξк=0,5. При плавном переходе сопротивление уменьшается. В расчетах целесообразнее ориентироваться на максимальные потери и брать значение, соответствующее входу без скругления (ξк=0,5).

4. Сопротивления в виде сетки ξс. Для замедления течения иногда применяют сетки, представляющие собой стержни в виде диафрагм с небольшими отверстиями. По аналогии с соответствующими устройствами в гидравлических системах можно принимать ξс ≈5,0.

5. Потери на трении о стенки каналов ξтр. Эти потери определяются по формуле:

где L – длина канала; D – диаметр канала; λ - коэффициент потерь на трение.

Данный коэффициент зависит от режима течения, определяемого критерием Рейнольдса и шероховатостью поверхности стенок канала. Шероховатость оценивается соотношением средней величины выступа на поверхности канала к его радиусу R ( /R). При заливке металла в

142

песчаную форму выступы на поверхности стенки образованы зернами формовочной смеси.

На основании изучения движения жидкостей по трубам с нормированной шероховатостью при ламинарном режиме получена зависимость:

В этой области шероховатость стенок не оказывает влияния на течение. В среднем можно считать, что коэффициент потерь на трение постоянен и равен λ=0,04. Следовательно, потери на трение при заполнении формы расплавом можно оценить по формуле

Для турбулентного режима заполнения можно принять следующую приближенную формулу для технологических расчетов коэффициента расхода литниковой системы:

где первый член суммы под корнем получается при сложении единицы с потерями на переходе из литниковой чаши в стояк (ξк=0,5); второй – произведение коэффициента потерь при повороте на 900 на число таких поворотов n; третий – произведение коэффициента потерь при соотношении площадей сечений элементов 0,8 ξсеч=0,15 на число таких изменений m; четвертый – произведение среднего значения коэффициента потерь на трение λ=0,04 на сумму отношений длин к диаметрам для всех элементов литниковой системы.

Значение коэффициента μ для различных сплавов и условий заливки выбирают из табл. 3.11 и 3.12.

143

Движение неметаллических частиц в потоке расплава и их задержание

Неметаллические частицы отличаются по плотности от металлических сплавов и обладают способностью к самостоятельному движению.

В сплавах на основе железа, меди и титана шлаки, флюсы и окислы всех компонентов легче, чем жидкие сплавы, и их частицы всплывают на поверхность потоков. В сплавах на основе алюминия и магния их окислы тяжелее расплавов и тонут в потоках. Исключения составляют окислы натрия, которые образуются при модифицировании алюминиевых сплавов. Флюсы в алюминиевых сплавах плавают на поверхности как более легкие; в магниевых сплавах они находятся на дне плавильных тиглей (табл. 3.13). Таким образом, борьба с неметаллическими частицами в тяжелых и легких сплавах должна производиться существенно различными методами. Эти различия должны быть учтены при конструировании литниковой системы.

144

Для частиц размером более 1 мм в железных сплавах скорость их всплывания при турбулентном режиме потока описывается законом Стокса:

где γм и γш – плотность расплава и неметаллических (шлаковых) частиц; d – диаметр частиц; g – ускорение силы тяжести; с – коэффициент, зависящий от критерия Re, а также соотношения размеров частиц и кана-

145

ла, в котором происходит их всплывание; его можно считать равным единице (с=1).

При всплывании неметаллических частиц в вертикальном канале (стояке) литниковой системы их отделение возможно только в случае, когда скорость всплывания больше скорости потока расплава. Расчеты показывают, что для чугунных отливок всплывать могут только крупные частицы (> 10 мм), а остальные уносятся с потоком в следующие элементы литниковой системы.

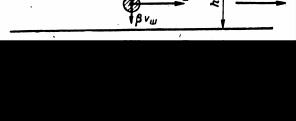
В горизонтальном потоке (рис. 3.19) траектория движения неметаллической частицы определяется скоростью всплывания W, направленной вверх, усредненной горизонтальной скоростью потока vш и вертикальной составляющей движения турбулентного потока. Эта статистическая величина, определяющаяся вихревым характером движения, может быть направлена как вверх, так и вниз. Величина вертикальной составляющей vв пропорционально средней горизонтальной скорости потока vш:

где β - коэффициент пропорциональности, равный примерно 0,2.

Рис. 3.19. Схема к расчету шлакоуловителя

146

Таблица 3.13

Плотности основ сплавов и неметаллических загрязнений

Для того чтобы неметаллические частицы были задержаны, необходимо, чтобы за время прохождения потока по всей длине шлакоуловителя даже те из них, которые сначала находились на дне, всплывали бы на полную высоту канала. Поскольку мы должны рассматривать наихудшие условия, будем считать, что вертикальная составляющая турбу-

147

лентного потока все время будет направлена вниз. Обозначим длину шлакоуловителя через Lш, а высоту литника через h. Тогда условие, обеспечивающее всплывание, имеет вид

Если скорость потока велика, а скорость всплывания мала, то это будет означать, что частицы соответствующего размера не будут задерживаться в шлакоуловителе. Они будут находиться в состоянии «витания».

Определим размеры шлакоуловителя, обеспечивающего задержание шлаковых частиц минимального размера dmin.

Металл из шлакоуловителя сечением Fш, текущий со скоростью vш, переходит в литник сечением Fл, в котором будет течь со скоростью vл. Исходя из условий неразрывности потока, можно написать

Cкорость течения металла через литник можно определить выражением

где G – масса отливки; γ - плотность металла; τ - время заполнения формы, определяемое из технологических соображений; m и n – некоторые коэффициенты.

Скорость течения в шлакоуловителе должна быть такой, чтобы поток металла не мог увлечь за собой частицы, уже всплывшие в его верхнюю часть. Это становится возможным, если скорость потока не превосходит некоторую предельную величину. Для шлаковых частиц диаметром dmin = 1 мм в потоке из жидкого чугуна критическая скорость, не мо-

148

гущая их извлечь из пристеночного слоя, составляет 40 см/с. Обозначим эту критическую скорость через Vш. кр. Тогда соотношение размеров сечения шлакоуловителя и литника, соответствующее условиям задержания шлаковых частиц, определяется равенством

где G – масса отливки, кг.

Полагая, что в выражении (3.47) правая и левая части равны друг другу, и решая его относительно длины, получаем:

Примем: dmin=1 мм; γ м=6,8 г/см3; γ ш=2,3 г/см3; β=0,2; vш.кр.=40 см/с.

Тогда

Таким образом, длина шлакоуловителя, на котором частицы диаметром больше 1 мм могут задерживаться, должна быть не меньше 32 высот питателя.

Выражения (3.51) и (3.52) позволяют ориентировочно определить размеры шлакоуловителей. Практически применяемые размеры этого элемента имеют тот же порядок величин.

149

На рис. 3.20 приведены схемы незапертой, запертой обычной и запертой с нижним подводом литниковых систем, а на рис. 3.21 – схемы специальных шлакоуловителей.

Рис. 3.20. Схемы незапертой, запертой обычной и запертой с нижним подводом литниковых систем

Рис. 3.21. Схемы специальных шлакоуловителей: а – тормозящие элементы; б – дроссель; в – фильтрующая сетка

Вопросы для самоконтроля знаний

1.Каковы основные режимы движения жидких металлов?

2.Что характеризует и как рассчитывается критерий Рейнольдса?

3.Как определяется жидкотекучесть металлов и сплавов?

4.Приведите классификацию способов заливки форм.

5.Укажите элементы литниковых систем.

6.Приведите классификацию литниковых систем по их расположению относительно отливки.

7.Каковы основные принципы проектирования литниковой системы?

150

8.Чем обусловлены выбор положения отливки в форме и места подвода металла в форму?

9.Опишите сужающиеся и расширяющиеся литниковые системы и их применение.

10.Каковы виды местных сопротивлений?

11.Как рассчитываются потери металлостатического напора?

12.Каковы способы задержания неметаллических частиц в потоке расплава?

Раздел 4. ВЗАИМОДЕЙСТВИЕ РАСПЛАВА С МАТЕРИАЛОМ ЛИТЕЙНОЙ ФОРМЫ. ФОРМИРОВАНИЕ ПОВЕРХНОСТИ ОТЛИВКИ

Формирование рельефа поверхности отливок

При заполнении песчаной формы в результате соприкосновения жидкого металла с поверхностью формы воспроизводится ее микрорельеф. При этом чем меньше размер зерен песка, тем меньше будет высота выступов на отливках, т.е. тем меньше будет шероховатость и выше чистота литой поверхности (рис. 4.1, а). При определенных условиях, т.е. при равенстве значений металлостатического напора жидкого металла и капиллярного противодавления в поверхностных слоях формы, существует прямая пропорциональная зависимость между радиусом зерен формовочного песка Rз и средней высотой выступов на поверхности отливки Hср (рис. 4.1, б).

Помимо размера зерен песка на чистоту литой поверхности влияют также температура заливки, теплофизические свойства (теплоаккумули-

рующая способность: вф = λфсфγф , где вф - коэффициент теплоаккуму-