
- •Оглавление:
- •Линейное программирование.
- •Геометрическая интерпретация
- •Алгебра симплекс – метода.
- •Математическое описание.
- •Ограничения
- •Представление пространства решений стандартной задачи линейного программирования.
- •Анализируя таблицу, легко заметить две закономерности:
- •Вычислительные процедуры симплекс-метода.
- •Оптимальное решение
- •Табличный метод.
- •Получение начального допустимого базисного решения.
- •Двойственная задача.
- •Нелинейное программирование.
- •Необходимые и достаточные условия существования экстремума.
- •Ограничения в виде равенств.
- •Ограничения в виде не равенств.
- •Итеративные методы. Постановка задачи.
- •Градиентный метод.
- •Метод наискорейшего спуска (подъема).
- •Алгоритм Ньютона.
- •Элементы динамичного программирования.
- •Основные понятия и обозначения.
- •Идеи метода динамического программирования
- •Введение в вариационное исчисление Основная задача вариационного исчисления
- •Классы функций
- •Экстремум функционала
- •Непрерывность и варьируемость функционала
- •Вариация функционала
- •Необходимое условие экстремума функционала
- •Основная лемма вариационного исчисления
- •Список литературы
Оглавление:
Линейное программирование………………………………………….ст. 2
Нелинейное программирование……………………………………….ст.13
Элементы динамичного программирования………………………….ст.19
Вариационное исчисление……………………………………………..ст.23
Список литературы……………………………………………….……..ст.34
Линейное программирование.
Постановка задачи
Термин и линейное программирование связывается со следующей задачей. Дана система линейно независимых уравнений с неизвестными х1,….,х2 – система ограничений задач и линейного программирования:
 ,
(1)
,
(1)
где bi≥0. Требуется найти неотрицательное значение переменных (хi≥0), которые удовлетворяют управлениям (1) и обращают в минимум целевую функциюq=c1x1+…+cnxn(2), называемой линейной формой.
Матричная запись:
 (3)
(3)
Если m<n, то система (1) имеет бесчисленное множество решений. Любое решение системы (1), гдеxi≥0 будем называть допустимым решением. Среди допустимых решений нужно выбрать такое, которое обращает в минимум целевую функцию.
В
ограничения (1) могут входить не равенства
aj1x1+..+ajnxn≤bjили aj1x1+..+ajnxn≥bjвведя дополнительную переменнуюxn+jтак, чтобы имело место:
aj1x1+..+ajnxn+xn+j=bjилиaj1x1+..+ajnxn-xn+j=bjчто не меняет существа задачи. Задача
максимизации сводится к рассмотренной
путем замены знака целевой функции![]() .
.
Базисом называют набор mпеременных таких, что определить, составленный из коэффициентов, при этих переменных не равен нулю. Эти переменных называют базисными. Если положить все свободные переменные равными нулю и решить полученную системуmуравнений сmнеизвестными, то получим базисное решение. Допустимыми базисными решениями являются такие, которые дают неотрицательные значения базисных переменных.
Геометрическая интерпретация
g=x2-x1(4)
при ограничениях
 .
(5)
.
(5)
Удобнее решить задачу максимизации q/= -q= x1-x2. (6)
Имеется
m=3 базисных переменных иn-m=2 свободных.
Выразим базисные переменные через
свободные
 .
.
Область
допустимых значений:
xi≥0,![]() .
Построим прямыеx3,x4,x5на плоскостиx1,x2:
.
Построим прямыеx3,x4,x5на плоскостиx1,x2:
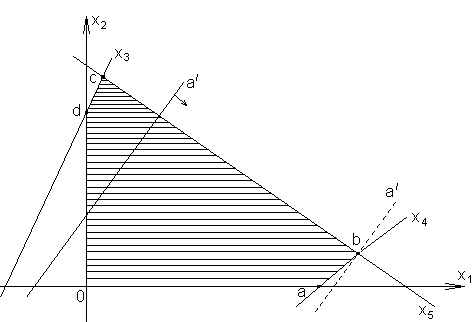
Для каждой прямой xiпеременныхxi=0. В точках пересечения 2-х прямых в нуль обращаются две переменные, что соответствует базисному решению. Вершины многоугольника допустимых решений соответствуют допустимым базисным решениям. Выражение (6) определяет прямую, причём увеличениеq/соответствует перемещению прямой в направлении стрелки. Эта прямая должна проходить через область допустимых решений. Максимумq/получим в крайнем положении прямой (пунктир). Таким образом, решение, обращающее в максимум целевую функциюq/, обязательно лежит среди допустимых базисных решений. Т.к. их число, конечно, то можно найти все допустимые базисные решения и для каждого из них вычислить значениеq/. Окончательным решением будет, то для которогоq/будет максимально.
Наиболее распространённый метод такого перебора решений – это симплекс – метод.
Алгебра симплекс – метода.
Существо метода состоит в следующем. Находим какое-нибудь базисное решение. Далее проверяем, не достигнут ли уже максимум целевой функции. Если нет, то ищем новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение q/. Затем процедуру повторяем. Для перехода к новому допустимому базисному решению одну из свободных переменных следует сделать базисной. При этом она станет отличной от нуля и будет возрастающей. Если какая либо свободная переменная входит в целевую функцию со знаком «+», т.е. при её увеличении целевая функция увеличивается, то максимум не достигнут и данную переменную следует сделать базисной (отличной от нуля).
