IK_ekz

Необходимо отметить, что, помещая на главной диагонали единицы, или корреляции каждой переменной с самой собой, мы учитываем полную дисперсию каждой переменной, представленной в матрице. Тем самым принимается во внимание влияние не только общих, но и специфичных факторов.

Наоборот, если на главной диагонали корреляционной матрицы находятся элементы 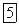соответствующие общностям и относящиеся лишь к общей дисперсии переменных, то учитывается влияние только общих факторов, элиминируется влияние специфичных факторов и ошибок, т. е. отбрасываются специфичность и дисперсия ошибок.

118. (6.16) Парная линейная регрессия, коэффициенты регрессии, способы расчета и графического представления.

Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1, Х2, … Хр и Y. При этом речь идет о влиянии переменных Х на значения переменной Y.

Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.

Парная регрессия – уравнение связи двух переменных у и x:

,

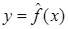где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор). Различают линейные и нелинейные регрессии.

Линейная регрессия:.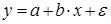

Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предварительная стандартизация факторных показателей, то b0 равняется среднему значению результативного показателя в совокупности. Коэффициенты b1, b2,

..., bn показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных уравнений).

Вычислительные аспекты Общая вычислительная задача, которую требуется решать при анализе методом множественной

регрессии, состоит в подгонке прямой линии к некоторому набору точек.

В простейшем случае, когда имеется одна зависимая и одна независимая переменная, это можно увидеть на диаграмме рассеяния.

Метод наименьших квадратов. На диаграмме рассеяния имеется независимая переменная или переменная X и зависимая переменная Y. Эти переменные могут, например, представлять коэффициент IQ . Каждая точка на диаграмме представляет данные одного студента, т.е. его соответствующие показатели IQ. Целью процедур линейной регрессии является подгонка прямой линии по точкам. А именно, программа строит линию регрессии так, чтобы минимизировать квадраты отклонений этой линии от наблюдаемых точек. Поэтому на эту общую процедуру иногда ссылаются как на оценивание по методу наименьших квадратов.

Уравнение регрессии. Прямая линия на плоскости (в пространстве двух измерений) задается уравнением Y=a+b*X; более подробно: переменная Y может быть выражена через константу (a) и угловой коэффициент (b), умноженный на переменную X. Константу иногда называют также свободным членом, а угловой коэффициент - регрессионным или B-коэффициентом. Доверительные интервалы

В многомерном случае, когда имеется более одной независимой переменной, линия регрессии не может быть отображена в двумерном пространстве, однако она также может быть легко оценена. Процедуры множественной регрессии будут оценивать параметры линейного уравнения вида:

Y = a + b1*X1 + b2*X2 + ... + bp*Xp

119. (6.17) Нелинейная статистическая связь, нелинейная регрессия, корреляционное отношение, коэффициент детерминации. Ранговая корреляция.

Связь Статистическая Нелинейная - статистическая связь между двумя или несколькими количественными переменными , не являющаяся линейной. В некоторых случаях С.С.Н. может быть описана, более или менее удовлетворительно, одной из нелинейных математических функций - логарифмической, экспоненциальной, полиномиальной, тригонометрической и т.п. Сила (теснота) парной нелинейной связи измеряется с помощью корреляционного отношения . Если нелинейная связь между двумя переменными имеет причинный характер, уравнение нелинейной связи является уравнением регрессии нелинейной.

Нелинейная регрессия — частный случай регрессионного анализа, в котором рассматриваемая регрессионная модель есть функция, зависящая от параметров и от одной или нескольких свободных переменных. Зависимость от параметров предполагается нелинейной. Корреляционное отношение (или коэффициент корреляции по Пирсону) применимое ко всем случаям корреляционной зависимости независимо от формы этой связи. Коэффициент корреляции

Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации r2) представляет долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных) .

Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными.

Коэффициент принимает значения из интервала 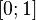. Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям.

В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату

коэффициента корреляции, то есть .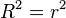

Иногда показателям тесноты связи можно дать качественную оценку

Функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50 %. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

Ранговая корреляция – метод корреляционного анализа, отражающий отношения переменных, упорядоченных по возрастанию их значения. Наиболее часто ранговая корреляция применяется для анализа связи между признаками, измеряемыми в порядковых шкалах ,а также как один из методов определения корреляции качественных признаков. Достоинством коэффициентов

ранговой корреляции является возможность их использования независимо от характера распределения коррелирующих признаков.

В практике наиболее часто применяются такие ранговые меры связи, как коэффициенты ранговой корреляции Спирмена и Кендалла. Первым этапом расчета коэффициентов ранговой корреляции является ранжирование рядов переменных . Процедура ранжирования начинается с расположения переменных по возрастанию их значений. Разным значениям присваиваются ранги, обозначаемые натуральными числами. Если встречается несколько равных по значению переменных, им присваивается усредненный ранг.

Применение ранговой корреляции:

1.Быстро ориентировочно определить связь между признаками.

2.Оценить связь между качественными и количественными признаками или между качественными.

3.Когда распределение значений учетных признаков не соответствует нормальному распределению или форма распределения неизвестна.

120.(6.18) Численные оценки статистической связи, основанные на принципах сопряженности: оценка взаимосвязи качественных признаков с помощью критерия хи-квадрат. Коэффициенты сопряженности, контингенции, Чупрова.

Коэффициенты сопряженности: коэффициенты Фишера-Филча, Крамера, Пирсона и Чупрова, величины которых всегда находятся в пределах от 0 до 1, вычисляются на основе различных вариантов соотношения критерия согласия Пирсона (хи-квадрат) и числа наблюдения. Математическая логика применения этих коэффициентов базируется на том, что если теоретическое распределение говорит о независимости(несвязности) признаков, то отклонение фактического распределения от теоретического будет тем больше, чем больше признаки взаимосвязаны. Это отклонение оценивается с помощью критерия хи-квадрат, который включен в формулы в качестве основного элемента. Сам по себе критерий хи-квадрат может свидетельствовать о наличии или отсутствии взаимосвязи, но его значение во много зависит от числа наблюдений. Значения хи-квадрат напрямую не могут использоваться для сравнения статистических связей в совокупности с разным числом наблюдений. Этот недостаток устраняется при использовании помимо численных значений хи-квадрата и числа наблюдений. Такие общие для всех коэффициентов особенности определяют их общие достоинства и недостатки: Достоинства: относительная простота получения оценок связи в таблицах сопряженности, где число строк и столбцов выходит за пределы 2х2(за исключением критерия Фишера-Филча), в том числе и в несимметричных таблицах Упрощение процедуры оценок статистической достоверности значений для этих критериев,т.к.

величина хи-квадрат,на основе которой эта достоверность оценивается используется как промежуточный результат вычислений. Т.е. не требуется специальных дополнительных расчетов для процедуры оценки репрезентативности полученных значений этих критериев.

Недостатки: ограничение области применения только таблицами, где данные представлены абсолютными числами Недопустимость применения при числе наблюдений в отдельных столбцах менее 5

Общее число наблюдений в таблице сопряженности не должно быть менее 50, а оптимальным считается 100 и более.

Критерий Пирсона хи-квадрат.

Хи-квадрат –один из наиболее распространенных критериев согласия. Его используют с различными формами распределений совокупностей. Как и любой другой статистический критерий, он не доказывает справедливость нулевой гипотезы, а лишь устанавливает с определенной вероятностью согласие или несогласие с данным наблюдением.

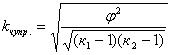
Величина критерия хи-квадрат – случайная величина,т.к. в различных опытах она принимает неизвестные ранее значения. Практическое вычисление критерия на конкретных данных, когда в качестве теоретического рассматривается нормальное распределение, вычисляется по таблице. Условие: не менее 5 наблюдений в каждой клетке таблицы. Если это условие не выполняется, необходимо сгруппировать частоты. После этого:

1.Вычисляется разность между частотами эмпирических и теоретических распределений.

2.Чтобы погасить отрицательные значения, эта разность возводится в квадрат.

3.Для уменьшения числового значения результата делится на величину эмпирических частот.

Число степеней свободы k, которое необходимо знать для оценки нулевой гипотезы, устанавливается в зависимости от вида распределения.(При биноминальном распределении k=S-2, при нормальном k=S-3, где S- число групп вариант с учетом объединения групп)

Полученное значение критерия хи-квадрат сравнивают с табличным или найденным с помощью компьютера теоретическим значением при заданном уровне сложности. Если вычисленный критерий больше табличного значения, то нулевая гипотеза, которая предполагает соответствие эмпирического и теоретического распределений, отвергается. Коэффициент Контингенции Пирсона - мера связи двух номинальных переменных на основе критерия хи-квадрат . Применяется, главным образом, к квадратным таблицам сопряженности размерности 3 * 3, 4 * 4 и т.п. Вычисляется по формуле C = Корень из х2 / (х2 n), где х2 - вычисленное по таблице сопряженности значение критерия хи-квадрат; n - объем выборки . При отсутствии статистической связи между переменными значение коэффициента равно 0; чем сильнее связь, тем ближе значение коэффициента к величине 1, однако максимальное значение коэффициента контингенции всегда меньше, чем 1. Коэффициент Чупрова-дает осторожные результаты, когда таблица сопряженности имеет

квадратную форму, а число строк и столбцов не превышает 5. Числитель-число строк,

К-число столбцов

http://www.kantiana.ru/medicinal/help/StatMethodsInClinics.pdf вдруг пригодится, вроде полезный ресурс 121. (7.1) Теоретические основы выборочных статистических исследований в доказательной

медицине. Понятие генеральной совокупности, выборки, репрезентативности выборки.

Статистическая (генеральная) совокупность - множество объектов, явлений, являющихся единицами статистического наблюдения, объединенных общими свойствами (признаками сходства). Отдельные единицы статистического наблюдения различаются между собой признаками различия.

Выборка - часть генеральной совокупности, подвергающаяся статистическому обследованию. Обязательное требование к выборке - ее репрезентативность (представительность).

Выборка бесповторная - статистическая выборка, в которой отдельные единицы наблюдения из генеральной совокупности могут встретиться только один раз.

Выборка повторная - выборка, в которой отдельные единицы наблюдения из генеральной

совокупности могут встретиться несколько раз.

Выборочная характеристика - приближенное значение какой-либо статистической характеристики генеральной совокупности, полученное на выборочной группе.

Математическая статистика рассматривает два варианта статистической оценки достоверности (репрезентативности) результатов:

Соответствуют ли параметры выборочной группы наблюдений параметрам генеральной совокупности. Т.е. достоверно ли отражают результаты наблюдения выборочной группы ситуацию в генеральной совокупности?

Относятся ли две группы наблюдений к одной совокупности или нет. Соответственно, различия в результатах наблюдений по этим группам носят случайный (если они из одной генеральной совокупности) или неслучайный характер (если они относятся к разным генеральным совокупностям)?

Статистическая репрезентативность выборки

Количественная репрезентативность определяется числом наблюдений, гарантирующим получение статистически достоверных данных. Здесь действует закон больших чисел - "чем больше наблюдений - тем результаты достоверней" или "чем больше число наблюдений, тем больше характеристики выборки приближаются к соответствующим характеристикам генеральной совокупности".

Качественная репрезентативность - обозначает структурное соответствие выборочной и генеральной совокупностей. Например: если в генеральной совокупности лиц мужского пола 50%, то и в выборочной группе их должно быть 50%.

Формирование выборочной совокупности

1.Случайный метод: Пример: лото

-повторный (без исключения)

-бесповторный (исключение одного из вариантов после выборки)

2.Типическая, типологическая, районированная выборка; (выборка по определенному признаку) Пример: народность - чукчи

3.Когортный метод отбора отдельных единиц, объединенных каким-либо событием;

Пример: женщины репродуктивного возраста 4. Парносопряженный метод копий-пары; (2 идентичные выборки, отличающиеся по 1

признаку)

Пример: близнецовый метод 122. (7.2) Стандартные ошибки для средних значений, относительных показателей.

Интервальные оценки параметров распределений. Доверительная вероятность. Доверительный интервал.

Стандартная ошибка - среднеквадратическое отклонение.

Отклонение среднеквадратическое, стандартное отклонение (сигма) - статистический критерий разнообразия признака, характеристика вариабельности, изменчивости признака, разброса вариант, однородности распределения случайной величины.

Среднеквадратическое отклонение - квадратный корень из дисперсии (статистического критерия разнообразия), применяется для:

1.Оценки вариабельности (изменчивости) однородных рядов распределения

2.Оценки типичности средних величин для данного ряда

3.Определения доверительных интервалов в параметрической статистике

4.Оценки репрезентативности выборочных исследований

5.Диагностической оценки показателей физического развития Вычисляется этот параметр в случае повторного отбора по формуле: m= ±√сигма/n, где

m – стандартное отклонение среднего значения (по аналогии со стандартным отклонением вариант от среднего вариационного ряда)

сигма – среднеквадратическое отклонение выборки (разброс значений) n – число наблюдений в выборке (объем выборки)

Чем больше сигма, тем больше ошибок; чем больше n, тем меньше ошибок.

Поскольку параметр m характеризует ошибку утверждения (ошибку прогноза) о том, что выборочное среднее равно генеральному среднему, то чем выше требование к вероятности этого вывода, тем шире должен быть обеспечивающий точность такого прогноза интервал, называемый

доверительным интервалом.

Недостаток этого критерия заключается в невозможности использования для сравнения разнородных величин.

Доверительная вероятность - вероятность, оценивающая достоверность статистических характеристик, полученных выборочным путем; величина доверительного интервала.

123. (7.3) Распределение Стьюдента. Расчет доверительных интервалов для средних значений.

Величина доверительной вероятности может задаваться доверительным параметрическим коэффициентом t – коэффициентом Стьюдента

При достаточно большом количестве наблюдений (>30) значения доверительного коэффициента t и доверительной вероятности соотносятся следующим образом:

При малых числах наблюдений значения коэффициента Стьюдента с учетом уровня доверительной вероятности можно установить по специальным таблицам.

Выбор того или иного уровня значимости или, соответственно, доверительной вероятности в общем является произвольным. В медико-биологических исследованиях допускается доверительная вероятность не менее 95.5 %. В этом случае доверительный интервал для средних при количестве наблюдений >30 равен ±2m. В целом, чем больше доверительная вероятность, тем больше доверительный интервал.

124. (7.4) Расчет доверительных интервалов для относительных показателей. Преобразование Фишера. (про Фишера только в этой теме нашла)

Дисперсионный анализ – статистический метод измерения взаимосвязи между результативным (количественным) и факторным (качественным) признаком. Позволяет оценить существенность влияния некоторого качественного фактора на изучаемую величину, точнее на ее количественные показатели (характеристики).

Оценка влияния нескольких факторных признаков – многофакторный анализ. Дисперсионный анализ применяется при:

1.нормальности распределения анализируемых групп или соответствии выборочных групп генеральным совокупностям с нормальным распределением.

2.Независимости (случайности) наблюдений в группе

Основная идея – сравнение разброса, зарегистрированных значений, вызванного воздействием факторного признака (фактора), с величиной разброса вызванного случайными обстоятельствами. Отклонение факторного признака больше, чем случайного признака => фактор оказывает существенное влияние на признак.

Общая дисперсия = дисперсия фактора + остаточная дисперсия

Добщ – характеризуется разбросом вариант от общего среднего

Дфакт – дисперсия фактора (разброс групповых средних от общего среднего)

Дост – внутригрупповая остаточная дисперсия (случайное рассеяние внутри групп) Этапы дисперсионного анализа:

1.вычисление средних квадратов отклонений

2.вычисление дисперсий

3.сравнение факторной и остаточной дисперсий – критерий Фишера

4.оценка этих соотношений с помощью теоритических значений распределения

125.(7.5) Обработка цензурированных наблюдений, анализ выживаемости.

(из интернета)

Под методами оценки выживаемости понимается изучение закономерности появления ожидаемого события у представителей наблюдаемой выборки во времени. Таким событием не обязательно является летальный исход, как можно предположить из названия

анализа. Им может быть рецидив заболевания или, наоборот, выздоровление, в общем случае

–происхождение определенного события. Точкой отсчета может быть дата (час) выполнения процедуры, назначения лекарственного препарата, возраст на момент диагноза и т.п.

Период времени от начального события (например, постановки диагноза) до итогового (летальный вариант исход, рецидив, выздоровление) называется временем до события или временем ожидания.

Данные, которые содержат неполную информацию, называют цензурированными. С такими выборками приходится иметь дело, когда наблюдаемый параметр является временем до наступления события, а период наблюдения ограничен (например, у пациента рецидив заболевания не обнаружен за 6 месяцев до того, как он переехал в другой город и дальнейшая информация о нем недоступна).

При анализе выживаемости, как и при других методах статистического анализа, вся информация о выборке содержится в соответствующей ей функции распределения вероятности (в данном случае

–времён ожидания), но используется она не в виде плотности распределения вероятности значений, а в виде функции выживания. Кумулятивная функция распределения F(t) времён ожидания отражает вероятность того, что время ожидания события меньше t. Соответственно, функция выживания S(t) = 1 – F(t) равна вероятности того, что событие не состоится ранее, чем по истечении времени t.

Наиболее распространенными описательными методами исследования цензурированных данных являются построение таблиц дожития и метод Каплана-Мейера.

126. (7.6) Проверка статистических гипотез как метод поддержки врачебных решений. Нулевая и альтернативная гипотезы. Понятие статистической значимости и его применение для выбора в пользу одной из гипотез.

Методология статистических гипотез

В статистике основную выдвигаемую гипотезу обычно называют НУЛЕВОЙ – Н0 Гипотезу, которая противоречит нулевой, называют

КОНКУРИРУЮЩЕЙ или АЛЬТЕРНАТИВНОЙ – Н1 Например, если одна гипотеза Н0 предполагает, что одно среднее арифметическое (М1) не равно

другому (М2), то её логическим отрицанием будет принятие альтернативной гипотезы Н1, признающей, что средние равны.

Н0: М1 ≠ М2 Н1: М1 = М2

Каждому значению доверительной вероятности соответствует уровень значимости P. Уровень значимости выражает вероятность нулевой гипотезы, т.е. вероятность того, что выборочная и генеральная средние не отличаются друг от друга.

Таким образом, статистическая значимость выборочных характеристик представляет собой меру уверенности в их «истинности». Уровень значимости находится в убывающей зависимости от надежности результата. Более высокая статистическая значимость соответствует более низкому уровню доверия к найденной в выборной характеристике. Именно уровень значимости представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю генеральную совокупность.

В практике медико-биологических исследований наиболее часто используются следующие значения показателей значимости: 0,1; 0,05; 0,01; 0,001. Традиционная интерпретация уровней значимости, принятая в этих исследованиях, представлена в таблице