IK_ekz

113. Численные оценки параметров распределения случайной величины, характеризующих центр распределения. Средние значения, их расчет, свойства, способы применения в медицинской статистике.

(стр. 203-219)

Важным свойством статистической совокупности является положение центра ряда распределения. Параметры распределения с помощью которых можно оценить величину сдвига, характеризуют распределение ряда положением его середины и называются средними величинами. Средняя величина выражает характерную типичную для данного ряда величину признака.

Средние величины:

Степенные средние:

-среднее арифметическое

-среднее гармоническое

-среднее квадратическое

-среднее геометрическое

Методика расчета простой средней арифметической

-Суммировать варианты: V1+V2+V3+...+Vn = Σ V;

-Сумму вариант разделить на общее число наблюдений: М = Σ V / n

Методика расчета взвешенной средней арифметической

-Получить произведение каждой варианты на ее частоту — Vp

-Найти сумму произведений вариант на частоты: V1p1 + V2p2+ V3p3 +...+ Vnpn = Σ Vp -Полученную сумму разделить на общее число наблюдений: М = Σ Vp / n

Методика расчета среднеквадратического отклонения

-Найти отклонение (разность) каждой варианты от среднеарифметической величины ряда (d

= V — М);

-Возвести каждое из этих отклонений в квадрат (d2);

-Получить произведение квадрата каждого отклонения на частоту (d2р);

-Найти сумму этих отклонений: d21p1 + d22p2 + d23p3 +...+ d2npn = Σ d2р;

-Полученную сумму разделить на общее число наблюдений (при n < 30 в знаменателе n-1): Σ d2р / n

-Извлечь квадратный корень: σ = √Σ d2р / n

-мода ( наиболее часто встречающаяся варианта. Дает представление о центре распределения вариационного ряда. Используется для определения: 1- центра распределения в открытых вар. рядах 2- среднего уровня в рядах исходных данных с резко ассиметричным распределением)

-медиана (серединная варианта, центральный член ранжированного ряда)

Применение средних величин для оценки состояния здоровья — например, параметров физического развития (средний рост,

средняя масса тела, среднее значение жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средняя величина пульса, средняя СОЭ и др.); для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических

учреждений, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений на 1 ч приема в поликлинике и др.); для оценки состояния окружающей среды.

114. Численные оценки параметров распределения случайной величины, характеризующих разброс значений вариационного ряда. Меры вариабельности, их расчет, свойства, способы применения в медицинской статистике. :

Показатели разброса и их практическое применение

-лимит – Lim (указывает границы вариационного ряда. Например, самый большой вес 95 кг, самый маленький 48 кг. Lim=(48÷95)кг)

-амплитуда- Amрl (Исчисляется как разность между максимальным и минимальным значениями признака: Ampl= 9548= 47 кг)

1-оценка вариабельности рядов распределения

2-факторный анализ (дисперсионный)

3-Статистическая оценка различий двух совокупностей с одинаковыми или близкими значениями средних (критерий Фишера)

-среднеквадратическое отклонение –(сигма) D

1-оценка данных однородных числовых рядов при близких средних: чем больше сигма, тем больше разброс значений, соответственно среднее арифметическое менее типично для данного ряда 2-оценки типичности среднего (правило 3х сигм) в изолированном ряду

3-определение доверительных интервалов стат. Коэффициентов и репрезентативности выборочных исследований 4-диагностическая оценка показателей физического развития

С 100%

1-сравнение вариабельности значений разноименных признаков 2-получение нормированных оценок вариабельности значений (малая, средняя, большая)

-Квантили (неведомая хрень)

115. (6.13) Численные оценки параметров, характеризующих отклонение изучаемых

распределений от нормального распределения (распределения Гаусса).

Оценка характера распределения:

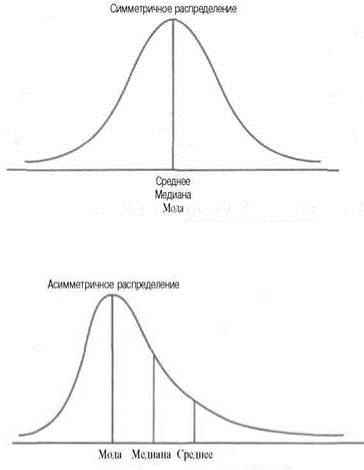
Первый способ: для нормального распределения характерно совпадение величин среднего арифметического, моды и медианы.

Второй способ: показатели асимметрии и эксцесса.

Асимметрия – это показатель симметричности/скошенности кривой распределения относительно среднего значения.

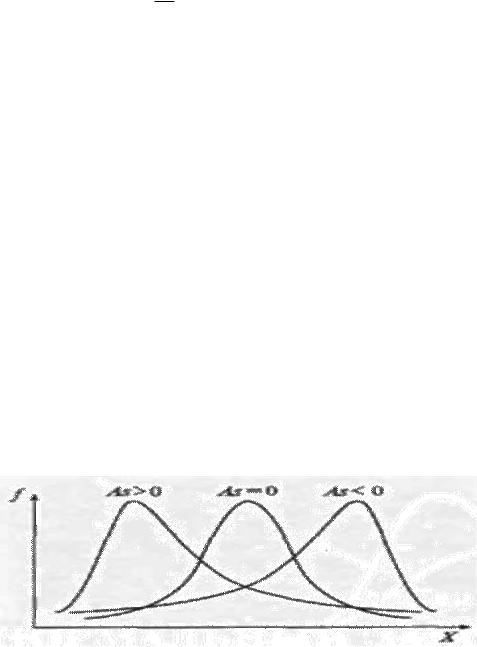
Асимметрия показывает, в какую сторону относительно среднего сдвинуто большинство значений распределения. Нулевое значение асимметрии означает симметричность распределения относительно среднего значения, положительная асимметрия указывает па сдвиг распределения в сторону меньших значений , а отрицательная асимметрия – в сторону больших значений . В большинстве случаев за нормальное принимается распределение с асимметрией, лежащей в пределах от -1 до +1.

Асимметрия: положительная (1); нулевая (2); отрицательная (3)

Эксцесс является мерой «сглаженности» («остро-» или «плосковершинности») распределения. Если значение эксцесса близко к 0, это означает, что форма распределения близка к нормальному виду. Положительный эксцесс указывает па «плосковершинное» распределение, у которого максимум вероятности выражен не столь ярко, как у нормального. Значения эксцесса, превышающие 5.0, говорят о том, что по краям распределения находится больше значений, чем вокруг среднего . Отрицательный эксцесс, напротив, характеризует «островершинное» распределение, график которого более вытянут по вертикальной оси, чем график нормального

распределения (рис.6.5.). Считается, что распределение с эксцессом диапазоне от -1 до +1 примерно соответствует нормальному виду. В тех случаях, когда какие-либо причины способствуют преимущественному появлению средних или близких к средним значений, образуется распределение с положительным эксцессом. Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двувершинное.

Третий способ: формулы Н.А. Плохинского и Е.И. Пустыльника для оценки типа распределения.

Чтобы оценить отличие теоретического распределения от нормального, необходимо сопоставить показатели асимметрии и эксцесса с их критическими значениями, полученными по формулам Н.А. Плохинского:

где п – объем выборки.

Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз.

,(6.5.)

,(6.6.)

или (2) Е.И. Пустыльника:

где п – объем выборки.

Распределение считается нормальным, если эмпирический результат абсолютной величины показателей асимметрии и эксцесса не превышает их критические значения или равен им.

принцип принятия-отвержения гипотезы о нормальности распределения:

Если в первой из этих систем хотя бы одно из неравенств не выполняется, то распределение считается отличающимся от нормального.

Следует отметить, что компьютере программы вычисляют показатели асимметрии и эксцесса и соответствующие им ошибки по более сложным формулам, при этом принцип принятия решения о типе распределения безусловно сохраняется.

Четвертый способ: критерий Колмогорова-Смирнова (λ)

Четвертый и пятый способы позволяют сопоставлять эмпирическое распределение признака с теоретическим – равномерным, нормальным или какими-либо иными.

Статистический критерий нормальности Колмогорова-Смирнова считается наиболее состоятельным для определения степени соответствия эмпирического распределения нормальному, равномерному или какому-то иному. Он позволяет оценить вероятность того, что данная выборка принадлежит генеральной совокупности с нормальным распределением. Суть метода заключается в сравнении эмпирического (наблюдаемого) распределения накопленных частот выборки с теоретическим (ожидаемым) распределением накопленных частот. Если эта вероятность р≤0,05, то данное эмпирическое распределение существенно отличается от нормального, а если р > 0,05, то делают вывод о приблизительном соответствии данного эмпирического распределения нормальному.

При этом следует учитывать, что при малых, но обычных для психологических исследований выборках (до 50 человек) критерий Колмогорова-Смирнова недостаточно чувствителен при определении даже весьма заметных «на глаз» отклонений от нормальности.

Пятый способ: критерий Пирсона( χ2)

Критерий χ2 применяется для сопоставления эмпирического распределения признака с теоретическим – равномерным, нормальным или каким-то иным.

Критерий χ2 отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях. Если эта вероятность р≤0,05, то данное эмпирическое распределение существенно отличается от нормального, а если р>0,05, то делают вывод о приблизительном соответствии данного эмпирического распределения нормальному. В качестве ожидаемого (теоретического) распределения выступает равномерное распределение объектов по градациям переменной, в отношении которой применяется критерий.

При использовании критерия следует учитывать, что объем выборки должен быть достаточно большим: п≥30. При п<30 критерий χ2 дает весьма приближенные значения. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: f>5. Это означает, что если число разрядов задано заранее и не может быть изменено, то мы не можем применять метод χ2, не накопив определенного минимального числа наблюдений. Выбранные разряды должны "вычерпывать" все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях. Необходимо вносить «поправку на непрерывность» при сопоставлении распределений признаков, которые принимают всего 2 значения. Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду. Сумма наблюдений по разрядам всегда должна быть равна общему количеству наблюдений.

116. (6.14) Численные оценки, используемые при изучении распределений, отличающихся от нормального. Квантили, их применение в медицинской статистике.

Формы распределения. Коэффициент асимметрии и эксцесса Любое реальное распределение можно изобразить схематически в виде кривой, воспроизводящей

основные особенности данного распределения. Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот, функционально связанных с изменением вариант.

Элементами распределения являются:

варианта

частота

В зависимости от вида кривых, изображающих распределение, выделяют несколько основных типов распределения:

одновершинные

многовершинные

Кодновершинным относятся те, в которых один, обычно центральный вариант, имеет наибольшую частоту (плотность распределения). Частоты же остальных вариантов убывают по мере удаления от центрального.

Если частоты убывают слева и справа от центрального значения одинаково, то такие распределения называются симметричными.

Если частоты убывают слева и справа от центра распределения с разной скоростью, то такие распределения называют асимметричными.

Многовершинные распределения — это распределения, в которых несколько центров, т. е. такие, у которых несколько максимумов частот.

Для однородных совокупностей, как правило, характерны одновершинные распределения. Многовершинность распределения свидетельствует о неоднородности изучаемого явления. В этом случае необходимо произвести перегруппировку данных с целью выделения более однородных групп.

Выяснение общего характера распределения предполагает, наряду с оценкой его однородности, вычисление показателей асимметрии и эксцесса.

Кривые распределения бывают:

1.симметричными

2.асимметричными.

Взависимости от того, какая ветвь кривой распределения вытянута, различают:

1.правостороннюю асимметрию

2.левостороннюю асимметрию.

Для характеристики степени асимметрии двух или нескольких рядов пользуются коэффициентом асимметрии.

График симметричного распределения симметричен относительно точки максимума.

2. Асимметрия положительна (As>0), если длинная часть кривой распределения расположена справа от моды (Мо). В этом случае соотношение между средней, медианой и модой нарушено:

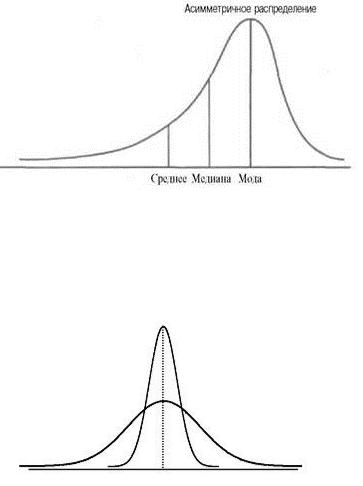
3. Асимметрия отрицательна (As<0), если длинная часть кривой распределения расположена

слева от моды (Мо).

As< 0.25 – слабая асимметрия

As= 0.25-0.5 – умеренная асимметрия

As> 0.5 – крайне асимметричное распределение

Для оценки «крутизны» (островершинности) распределения пользуются характеристикой – эксцессом.

Коэффициент эксцесса: Коэффициент эксцесса (коэффициент островершинности) — мера остроты пика распределения случайной величины.

Квантили.

В некоторых видах распределений среднеквадратическое отклонение и дисперсия отсутствуют или не могут служить характеристиками рассеяния вариант по др. причинам. Поэтому для сжатого описания такого рода распределений используют параметр разброса-квантиль.(перцентиль, персентиль), пригодный для статистического описания качественных или количественных признаков в любой форме их распределения. Этот параметр может использоваться для перевода количественных признаков в качественные. В этом случае качественные оценки присваиваются в зависимости от того, какому по порядку квантилю соответствует та или иная конкретная варианта. Особым свойством квантилей является их полная независимость от конкретных значений каждой отдельно взятой единицы наблюдения. Значение имеет только порядковый номер, месторасположение этой единицы в ряду распределения. Понять статистическую суть квантилей помогает графический метод, т.е. построение диаграммы распределения частот значений признака квантилях, которые могут выражаться в % или долях от единицы.

Использование для оценки показателей физического развития.

117. (6.15) Способы анализа взаимосвязей различных явлений. Статистическая и функциональная связь. Численные оценки статистической связи, основанные на принципах ковариации: коэффициенты линейной корреляции, частной (парциальной) и множественной корреляции. Корреляционная матрица.

Различают два типа связей между различными явлениями и их признаками: функциональную или жестко детерминированную, с одной стороны, и статистическую или стохастически детерминированную с другой.

Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной.

Функциональная связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более. В реальной природе (и тем более в обществе) таких связей нет.

Однако в науке используют представление связей как функциональных не только в аналитических целях, но нередко и в целях прогнозирования. Это возможно потому, что в простых системах интересующая нас переменная величина зависит в основном (скажем, на 99\% или даже на 99,99\%) от немногих других переменных или только от одной переменной. То есть связь в такой несложной системе является хотя и не абсолютно функциональной, но практически очень близкой к таковой.

Статистическая связь не имеет ограничений и условий, присущих функциональной связи. Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону связь является статистической. Иными словами, при статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.

Ключевые принципы численной оценки статистической связи Принцип ковариации. - Описывает параллельное изменение двух или нескольких

количественных признаков (характеристик). В математическом отношении задача сводится к определению числовых мер взаимных изменений этих характеристик – коэффициентов корреляции.

Принцип взаимной сопряженности - Описывает связь между появлением одного события с появлением других событий. Вероятность этой связи описывается с помощью коэффициентов сопряженности

Статистическую связь можно разделить на 2 вида: корреляционную связь и сопряжение. Корреляционной связью называют важнейший частный случай статистической связи,

состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака х закономерным образом изменяется среднее значение признака у; в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.

Коэффициент линейной корреляции Коэффициент корреляции Пирсона

Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона.

Частные коэффициенты корреляции служат для оценки вклада во множественный коэффициент корреляции каждого из факторов. Частный коэффициент корреляции является мерой линейной зависимости между двумя случайными величинами из некоторой совокупности случайных величин в том случае, когда исключено влияние остальных. Значительная величина межфакторной связи приводит к тому, что коэффициенты частной и парной корреляции отличаются друг от друга, хотя выводы о направлении связи на основе коэффициентов парной и

частной корреляции можно сделать одинаковые. Следовательно, коэффициенты частной корреляции более точно характеризуют связь между величинами.

Частный (парциальный) коэффициент корреляции выражает связь между двумя переменными при исключенном (элиминированном) влиянии еще одной или несколко других переменных. В простейшем случае частный коэффициент корреляции вычисляется как функция парных корреляций (произведений моментов) между Y, X1 и Х2.

Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей Коэффициент множественной корреляции принимает только положительные значения в пределах

от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем зависимость меньше. При значении R < 0,3 говорят о малой зависимости между величинами. При значении 0,3 < R < 0,6 говорят о средней тесноте связи. При R > 0,6 говорят о наличии существенной связи.

Квадрат коэффициента множественной корреляции называется коэффициентом детерминации Коэффициент детерминации показывает, какая доля вариации результативного показателя связана с вариацией факторных показателей. В основе расчета коэффициента детерминации и коэффициента множественной корреляции лежит правило сложения дисперсий, согласно которому общая дисперсия равна сумме межгрупповой дисперсии и средней из групповых дисперсий Межгрупповая дисперсия характеризует колеблемость результативного показателя за счет

изучаемого фактора, а средняя из групповых дисперсий отражает колеблемость результативного показателя за счет всех прочих факторов, кроме изучаемого.

Корреляционная матрица

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Корреляционная матрица характеризует взаимосвязь исходных признаков при факторном анализе

Матрица коэффициентов корреляции, полученных, как правило, экспериментальным путем, называется матрицей корреляции, или корреляционной матрицей.

Элементы этой матрицы являются коэффициентами корреляции между всеми переменными данной совокупности.

Если мы имеем, например, набор, состоящий из тестов, то число коэффициентов корреляции, полученных экспериментальным путем, составит

Эти коэффициенты заполняют половину матрицы, находящуюся по одну сторону ее главной

диагонали. По другую сторону находятся, очевидно, те же коэффициенты, так как и т. д. Поэтому корреляционная матрица симметрична.

На диагонали этой матрицы находятся единицы, поскольку корреляция каждой переменной с самой собой равна +1.

Матрица корреляции, у которой элементы главной диагонали равны 1, называется «полной матрицей» корреляции