Вариант №9

Задание №1 Найти матрицу С, если: С=2А(А-В)^Т , А=, В=.

Задание №2 Решить систему линейных уравнений методами:

• по формулам Крамера ,

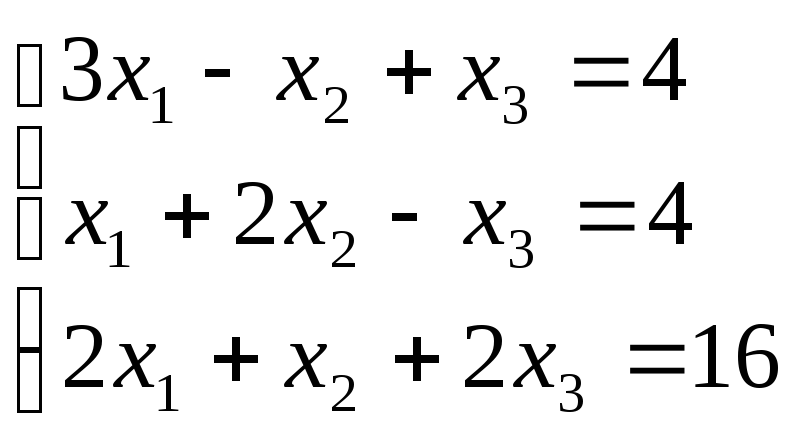
• методом Гаусса.

Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

• длину стороны АВ;

• общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых;

• косинус внутреннего угла при вершине В;

• уравнение медианы АЕ;

• уравнение и длину высоты СD;

• уравнение прямой, проходящей через точку Е параллельно стороне АВ;

• площадь треугольника АВС.

А (2,3); В (-1,2); С (-4,-4).

Задание №4 Вычислить пределы: _;

;

;

Задание №5 Найти производные функций: 1.2.

4.

5.

6.

Вариант №10

Задание №1 Найти матрицу С, если: С=А^Т (В+А), А=, В=.

Задание №2 Решить систему линейных уравнений методами:

• по формулам Крамера,

• методом Гаусса.

Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:

• длину стороны АВ;

• общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых;

• косинус внутреннего угла при вершине В;

• уравнение медианы АЕ;

• уравнение и длину высоты СD;

• уравнение прямой, проходящей через точку Е параллельно стороне АВ;

• площадь треугольника АВС.

А (3,3); В (-1,1); С (0,-7) .

Задание №4 Вычислить пределы: _;

;

;

Задание №5 Найти производные функций: 1. 2.

4.

5.

6.

Рекомендуемый список литературы

1. Высшая математика для экономистов : учебник для студ. вузов / Ред. Н.Ш. Кремер. - 3-е изд. - М. : ЮНИТИ, 2010. - 479 с.

2. Кремер, Н.Ш. Высшая математика для экономистов : практикум : учеб. пособие для студ. вузов, обуч. по экономическим спец. / Н. Ш. Кремер. - 2-е изд., перераб. и доп. - М. : ЮНИТИ, 2010. - 478 с.

3. Красс, М.С. Основы математики и ее приложения в экономическом образовании: учеб. для вузов / М.С. Красс, Б.Н. Чупрынов. - М.: Дело, 2005. - 452с.

26