Дано:Решение Смещение материальной точки при гармоническом колебании м

м

А  ?

Преобразуем уравнения, заданные в условии задачи, к такому же виду: м им. Из сравнения уравнений находим для первого колебания: амплитуда= 0,01 м, начальная фазарад = 30⁰; для второго колебания: = 0,02 м,рад = 90⁰. Частота колебаний одинакова, следовательно, и циклическая частота результирующего колебания тоже равна  . Для определения амплитуды результирующего колебания построим векторные диаграммы колебаний.

По теореме косинусов:

;

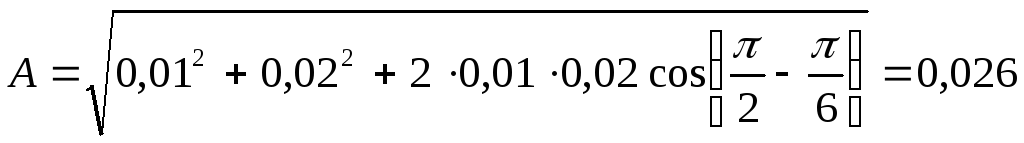м.

Тангенс начальной фазы результирующего колебания определим из рис. 23.5.

;

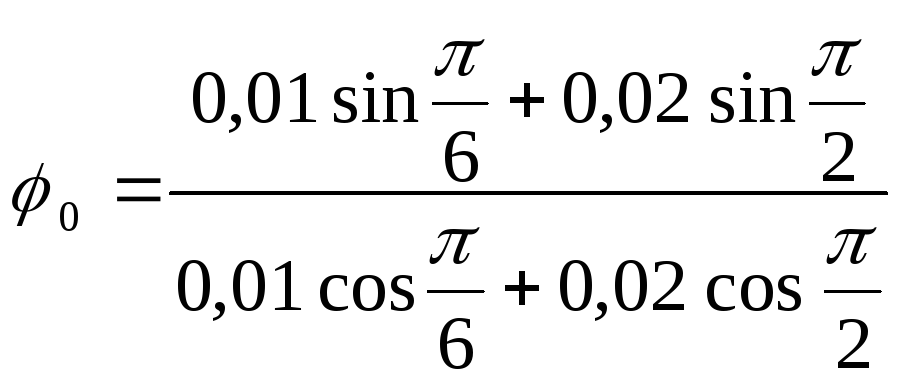= 2,88.

Откуда начальная фаза рад.

Уравнение смещения результирующего колебания

м.

Ответ: А = 0,026 м; рад.

Задача 5. Дифференциальное уравнение затухающих колебаний

. Найти коэффициент затухания, циклическую частоту, период, время релаксации, логарифмический декремент затухания.

Дано:Решение

Приведем данное уравнение к стандартному

?   ? Т  ? виду, и сравним с заданным уравнением

  ?   ?

и .

Из сравнения находим:  = 0,25 с^-1; ,= 4.

Частота  затухающих колебаний

с^-1  4 с^-1; .

Период затухающих колебаний можно считать равным периоду собственных колебаний

с.

Логарифмический декремент затухания .

Время релаксации

с.

Ответ:  = 0,25 с^-1;  = 3,99 с^-1; Т = 1,57 с;  = 4 с;  = 0,4.

Задача 6. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания  = 1,6, начальная фаза рад. Смещение колеблющейся точки в момент времени = 1 с равно = 4,5 см. Написать уравнение смещения в тригонометрическом виде.

Дано: Решение

Т

Уравнение смещения затухающих колебаний в тригонометрическом виде

.

Неизвестны коэффициент затухания  и амплитуда .

= 4 с

 = 1,6

рад

t = 1 с

= 4,5 см = 0,045 м

x(t)  ?

Коэффициент затухания  находим через логарифмический декремент затухания  =  Т, откуда ; с^-1.

Циклическая частота колебаний связана с периодом зависимостью ; .

Для нахождения максимальной амплитуды запишем уравнение смещения в момент времени , используя найденные значения величин. Получаем

откуда

м.

Ответ: уравнение смещения имеет вид м.

Задача 7. Чему равен логарифмический декремент затухания математического маятника длиной l = 1 м, если за 1 минуту амплитуда колебаний уменьшилась в два раза?

Дано:Решение

Логарифмический декремент затухания

l = 1 м , (1)

где   коэффициент затухания, Т – период колебаний.

= 1 мин = 60 с

  ?

Для математического маятника

, (2)

где l – длина маятника, g – ускорение свободного падения.

Амплитуда затухающих колебаний с течением времени изменяется по закону . Тогда.

Откуда

ln ; так как= 2, то

ln 2 = β t₁ ; . (3)