Дифференциальное уравнение гармонических колебаний

. (23.9)

Корнями решения этого уравнения являются выражения (23.1).

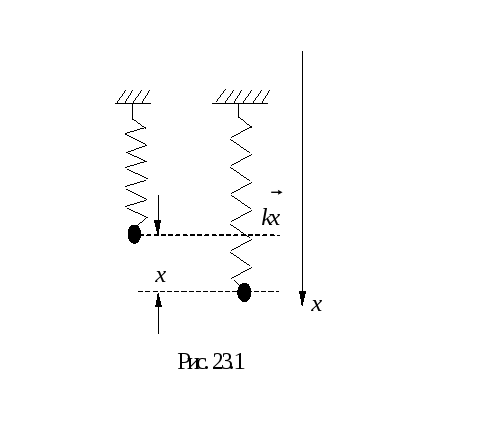
Рассмотрим колебания пружинного маятника. Состояние равновесия будем рассматривать как исходное положение пружинного маятника, а все дальнейшие смещения его оценивать координатой х, отсчитываемой от положения равновесия рис.23.1. Предположим, что никакие внешние силы колебаниям маятника не предшествуют. В этом случае на маятник, смещенный из положения равновесия, действует восстанавливающая сила F =  k x. Согласно 2-му закону Ньютона

F = m a,

где  ускорение маятника.

Но F =  k x, следовательно или.

Обозначим , тогда дифференциальное уравнение гармонического колебания примет вид

, (23.10)

а смещение из положения равновесия выразится, например, уравнением

. (23.11)

Скорость и ускорение материальной точки выразятся уравнениями (23.12) и (23.13):

; (23.12)

. (23.13)

Кинетическая энергия материальной точки, совершающей гармонические колебания, равна

. (23.14)

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием квазиупругой силы, равна

. (23.15)

Сложив и, получим формулу полной энергии:

.

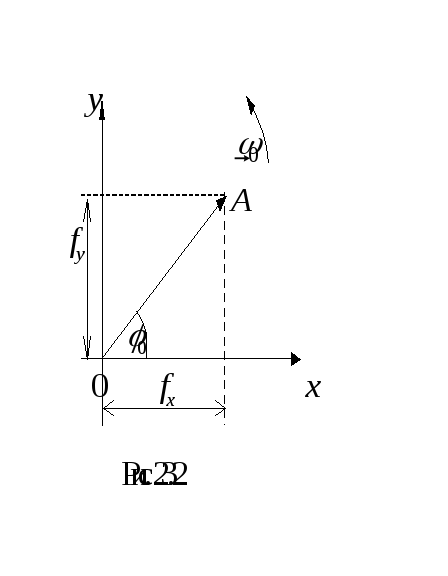
Гармонические колебания изображаются графически методом вращающегося вектора амплитуды или методом векторных диаграмм. Для этого из произвольной точки 0, выбранной на оси х, под углом , равным начальной фазе колебания, откладывается вектор, модуль которого равен амплитудеА рассматриваемого колебания (рис. 23.2). Если этот вектор привести во вращение с угловой скоростью , то проекция конца векторабудет перемещаться по осих и принимать значения от А до А, а колеблющаяся величина будет изменяться со временем по закону

.

Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания нужно сложить. Сложим гармонические колебания одного направления и одинаковой частоты:

;

,

воспользовавшись методом вращающегося вектора амплитуды. Построим векторные диаграммы этих колебаний (рис. 23.3).

Амплитуда и начальная фаза результирующего колебания задаются соотношениями

; (23.16)

. (23.17)

Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях:

. (23.18)

Если начальные фазы искладываемых колебаний одинаковы, то уравнение (23.18) примет вид

. (23.19)

Это уравнение эллипса, оси которого совпадают с осями координат, а полуоси равны соответствующим амплитудам.

Если , то эллипс (23.19) вырождается в окружность.

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системы. Свободные колебания реальных систем всегда затухают.

Дифференциальное уравнение свободных затухающих колебаний имеет вид

, (23.20)

где f – колеблющаяся величина, описывающая тот или иной физический процесс;  - коэффициент затухания; - циклическая частота свободных незатухающих колебаний той же колебательной системы.

Решение уравнения (23.20) в случае малых затуханий :

, (23.21)

где  амплитуда затухающих колебаний, а  начальная амплитуда.

Для пружинного маятника массой т, совершающего малые колебания под действием упругой силы F =  k x, коэффициент затухания

,

где r – коэффициент сопротивления.

Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшится ве = 2,71 раз, называется временем релаксации.

Период затухающих колебаний

. (23.22)

Если и амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его логарифм

логарифмическим декрементом затухания.