5. Оценка случайной погрешности

Случайную погрешность величины Xможно оценить, только проведямногократые измеренияX– не менеечетырёх измерений. Это означает, что процедуру измеренияXнадо проделать не менее четырёх раз, причём обязательно в одних и тех же условиях¹. Если бы никакие случайные факторы не влияли на результаты измерений, то сколько бы раз не повторялась процедура измеренияX, все результаты были бы совершенно идентичными. Наличие случайных факторов приводит к тому, что серия изnизмерений даётnразных значений величиныX: (x_,x_, ...,x_n)². То, насколько велик разброс в этихnчислах, и определяет случайную погрешность. Формула, по которой оценивают случайную погрешность_с(x), имеет вид:

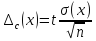. (1.7)

Здесь величина tназываетсякоэффициентом Стьюдента. Как его определить, рассмотрено в пункте 1.6. Величина(x) называетсясреднеквадратичным(илистандартным) отклонением и определяется выражением

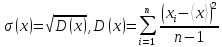, (1.8)

где 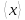– средний результат измерения, то есть среднее арифметическое изnчиселx_,x_, ...,x_n:

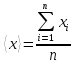, (1.9)

а число D(x) называется дисперсией³.

В пункте 1.6 отмечается, что с ростом объёма серии nкоэффициент Стьюдента уменьшается. Поэтому из формулы (1.7) вытекает:чем больше объём серии, тем меньше случайная погрешность. Обычно объём серии выбирают так, чтобы случайная погрешность былав три-пять раз меньшеприборной погрешности.

6. Доверительная вероятность и коэффициент Стьюдента

Будем в этом пункте считать, что приборная погрешность равна нулю. Тогда 2_c– этоширина доверительного интервала. В пункте 1.1 предполагалось, что в центре доверительного интервала находитсяистинное значениеxизмеряемой величиныX. Истинное значение, однако, неизвестно, поэтому передвинем доверительный интервал так, чтобы в центре его находилосьсреднее значениерезультатов измерения.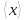

Вероятность того, что истинное значение x измеряемой величиныXпринадлежит доверительному интервалу шириной 2_сс центром в точке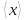, называетсядоверительной вероятностьюилинадёжностью измерений.

Ясно, что чем шире доверительный интервал 2_с, тем больше и доверительная вероятностьp. Верно и обратное: чем больше требование к надёжности измеренийp, тем больше и значение случайной погрешности_с. Связь междуpи_сопределяется формулой (1.7), в которой коэффициент Стьюдентаtзависит от доверительной вероятностиp.

Таблица 1.1.

Коэффициенты Стьюдента

Объём серии n	Доверительная вероятность p
	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99
4	0,77	0,98	1,2	1,6	2,4	3,2	4,5	5,8
5	0,74	0,94	1,2	1,5	2,1	2,8	3,7	4,6
6	0,73	0,92	1,2	1,5	2,0	2,6	3,4	4,0
7	0,72	0,90	1,1	1,4	1,9	2,4	3,1	3,7
8	0,71	0,90	1,1	1,4	1,9	2,4	3,0	3,5
9	0,71	0,89	1,1	1,4	1,8	2,3	2,9	3,4
10	0,70	0,88	1,1	1,4	1,8	2,3	2,8	3,3
15	0,69	0,87	1,1	1,3	1,8	2,1	2,6	3,0
20	0,69	0,86	1,1	1,3	1,7	2,1	2,5	2,9

Как видно из таблицы 1.1, на коэффициент Стьюдента влияет, кроме доверительной вероятности, ещё и объём серии n: чем большеn, тем меньшеt. В учебном лабораторном практикуме рекомендуется выбирать значение доверительной вероятностиp= 0,9, а объём серииn– от 5 до 10.

Пример. Требуется измерить сопротивление резистораRс надёжностьюp= 0,9. Для этого подготовлена таблица 1.2, а затем проделана серия из 10 измерений, полученные значения (частныерезультаты) записаны во втором столбце таблицы. Внизу столбца записано среднее значение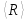, которое и считаетсяконечнымрезультатом измерения сопротивления.

Таблица 1.2.