Пример: нахождение точек экстремума функции и длины кривой
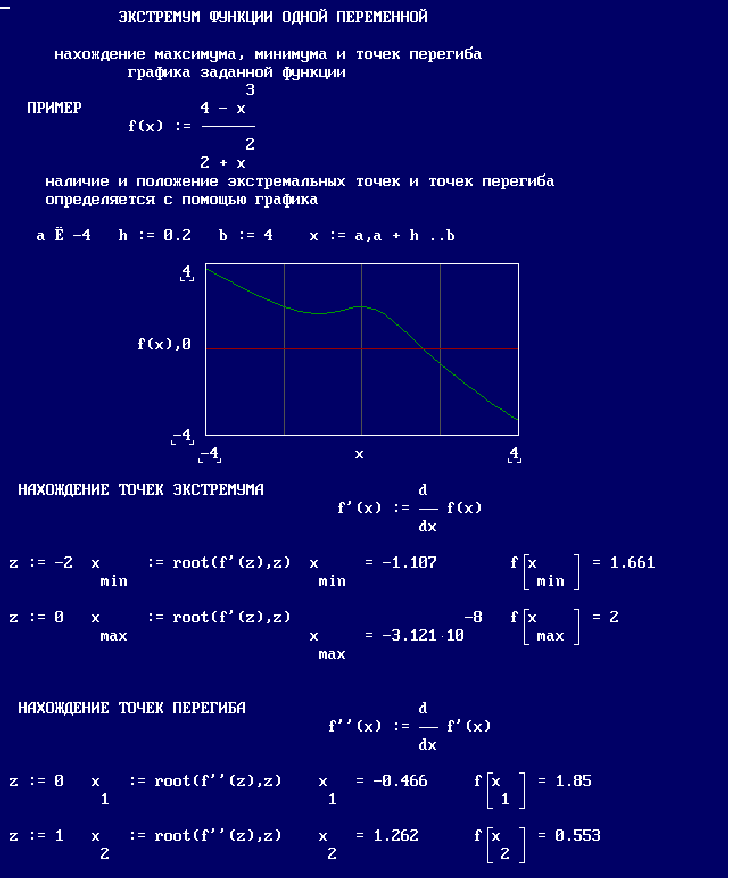
Применение функции вычисления производной, определенного интеграла и нахождения нуля функции.
Рассматривается применение функций вычисления производной, определенного интеграла и нахождения нуля функции на следующем примере: для заданной функции f(x) на заданном промежутке [a, b] найти точки экстемумаи длину дуги кривой, соединяющей эти точки.
На первом этапе строится график функции на заданном промежутке для визуального определения наличия точек экстремума и их положения. Для большей наглядности график снабжен изображением горизонтальной и вертикальной осей координат. В данном случае пары соответствующих обозначений абцисс и ординат в рабочей области графика представляют:
x, f(x) - график функции;
0, x - горизонтальная ось координат;
z, 0 - вертикальная ось координат.
Соответствующий фрагмент MathCAD-документа:
Далее, используя необходимое условие экстремума непрерывно дифференцируемой функции ( f '(x)=0 ), определяются абциссы точек максимума и минимума и значения функции в этих точках:
Наконец, по соответствующей формуле вычисляется длина дуги:
Преобразования Фурье
Быстрое преобразование Фурье. Функция, осуществляющая преобразование комплексных данных.
Обратное преобразование Фурье.
Функция, осуществляющая обратное преобразование комплексных данных.
Быстрое преобразование Фурье
Функция имеет вид:
fft(array)
Аргумент функции - имя массива. Индексация массива начинается с нуля, число элементов nмассиваarrayдолжно быть степенью 2: 32, 64, 128 и т.д. Если же число элементов массива не является степенью 2, то элементы с номерами, следующими за последней степенью 2, игнорируются.
Результат вычисления функции - массив размерности n/2+1, содержащий комплексные числа - коэффициенты дискретного преобразования Фурье, вычисляемые по формуле:
Функция, осуществляющая преобразование комплексных данных, имеет вид:
cfft(array)
Обратное преобразование Фурье
Функция имеет вид:
ifft(array)
Аргумент функции - имя массива. Индексация массива начинается с нуля. Число элементов nмассиваarrayдолжно быть больше степени 2 на один, например: 33, 65, 129 и т.д. Элементы с номерами, следующими за последним из таких чисел, игнорируются.
Результат вычисления функции - массив с числом элементов 2(n-1).
Функция icfft(array)осуществляет обратное преобразование комплексных данных.
Замечание: Аргумент и результат комплексного преобразования Фурье являются векторами с одинаковым числом элементов (степень 2).
Статистическая обработка данных
Среднее значение элементов массива.
Выборочная дисперсия.
Стандартное квадратичное отклонение.
Гистограмма.
Коэффициент корреляции.
Простые оценки (статистики)
mean(array)- среднее значение элементов массива,
var(array)- выборочная дисперсия,
stdev(array)- стандартное квадратичное отклонение,
Аргумент arrayфункций является именем массива. Нумерация элементов массива начинается с нуля (если параметрORIGINне был переопределен).
Гистограмма
Формат функции: hist(array1,array2)
Первый аргумент функции array1- массив, задающий пределы интервалов.
Пример задания массива array1. Пусть отрезок[1,8]разбит на 4 интервала:[1,3),[3,5),[5,7),[7,8]. Тогда массивarray1 можно задать следующим образом:
Второй аргумент функции array2- массив, содержащий данные. Результатом функции является массив частот, определяющих, сколько значений массиваarray2содержится в каждом из интервалов:
Размерность массива-результата array2 на единицу меньше размерности массиваarray1.