Встроенные средства системы MathCad для решения некоторых математических задач

Математические встроенные функции

Нахождение нулей функции. Встроенная функция root

Решение блоков. Функции Find и Minerr

Интерполяция функций

Оператор вычисления производной

Оператор вычисления определенного интеграла

Пример: нахождение точек экстремума функции и длины кривой

Преобразования Фурье

Статистическая обработка данных

Математические встроенные функции

• Вычисление значений функции Бесселя I-го и II-го рода целого индекса.

• Интеграл ошибок.

• Г-функция Эйлера.

• Нормированная функция распределения нормальной случайной величины.

Бесселевы функции

Функции Бесселя относятся к классу так называемых специальных функций, используемых в частности при решении задач математической физики. В MathCADе реализовано вычисление значений функций Бесселя I-го и II-го рода целого индекса.

Бесселевы функции 1-го рода: J0(x), J1(x), Jn(n,x),

где x- вещественное число,n- целое число,n>1.

.

Бесселевы функции 2-го рода: Y0(x), Y1(x), Yn(n,x),

где x- положительное вещественное число,n- целое число,n>1.

Замечание: Cм. Справочник по специальным функциям /Под ред. М.Абрамовица, И.Стиган. М.:Наука, 1979.

 

Специальные статистические функции

Данная версия системы содержит три специальные функции, связанные в первую очередь с расчетами в области математической статистики.

 

erf(x)- интеграл ошибок

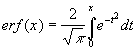
Г(x)- Г-функция Эйлера

cnorm(x)- нормированная функция распределения нормальной случайной величины

 

Нахождение нулей функции. Встроенная функция root

• Встроенная функция нахождения нулей функции.

• Изменение точности вычислений.

Нулем функции одной независимой переменной называется такое значение ее аргумента, при котором значение функции равно нулю, т.е. нуль функции f(x)- это корень уравненияf(x)=0.

Для поиска нулей функции, а также корней уравнения применяется встроенная функция root. Формат функции:

root(выражение,имя_переменной)

Чтобы найти нуль функции (или корень уравнения):

1) задайте начальное предполагаемое значение неизвестного,

2) используйте функцию root для решения.

Например, организовать поиск корня уравнения x3+x+1=0можно следующим образом:

x:=0.5 zeroval:=root(x3+x+1,x)

Замечание: В MathCADе решение уравнения ищется приближенно методом секущих. Находится действительный или комплексный корень в соответствии с типом начального приближения. Условием прекращения вычислений является (TOL встроенная переменная, ее значение по умолчанию 0.001,xn- значение функцииroot, f(xn) - значение выражения). При этом необходимое для начала итераций по методу секущих кромеx0 еще одно приближениеx1определяется по формулеx1=x0+h, где h= TOL, еслиx0 = 0, иначеh =x0 TOL. Другим условием прекращения вычислений является превышение определенного количества итераций, при этом выдается диагностическое сообщение'not converging'. Изменить точность вычисления можно, задав новое определение встроенной переменной TOL.

Сообщение "not converging" (нет сходимости) может появиться по следующим причинам:

1) функция не имеет нулей;

2) нули функции значительно удалены от указанного начального приближения;

3) между начальным приближением и нулями есть локальный минимум или максимум;

4) нарушается непрерывность выражения на промежутке между начальным приближением и нулем.

 

Лучший способ установить причину ошибки - построить график функции. Если функция имеет несколько нулей, укажите различные к ним начальные приближения.