Практическое занятие № 8.

Решение обыкновенных дифференциальных уравнений. Задача Коши.

1.Задача Коши

1.1.Одношаговые методы

1.2.Многошаговые методы

2.Решение задачи Коши средствами Mathcad

3.Символьное решение линейных дифференциальных уравнений

4.Порядок выполнения работы

5.Контрольные вопросы  

6.Задания для самостоятельной работы

 

1.Задача Коши .

Задачу Коши можно сформулировать следующим образом:

пусть дано ОДУ:

(1)

и начальное условие

. (1.1)

Требуется найти функцию , удовлетворяющую как указанному уравнению, так и начальному условию.

Численное решение задачи Коши состоит в построении таблицы приближенных значений y₀ , y₁ , y₂ , ..., y_n решения уравнения в точках

x₀ , x₁ , x₂ , ..., x_n .

Чаще всего

х_i = x₀ + ih , i = 0, 1, ..., n,

где h - шаг приращения переменной x,

n - число интервалов решения с шагом h.

Рассмотрим здесь две группы численных методов решения задачи Коши: одношаговые и многошаговые.

1.1.Одношаговые методы

Одношаговые методы - это методы, в которых для нахождения следующей точки на кривой y = f(x) требуется информация лишь об одном предыдущем шаге.

Метод Эйлера .

Метод Эйлера - простейший одношаговый метод. Его можно выводить из разных соображений.

Например, пусть - скалярная непрерывно дифференцируемая функция, т.е. в каждой точкесуществует производная

.

Тогда при малых

,

и выражение может использоваться в качестве разностной аппроксимации для первой производной.

Рассмотрим задачу Коши для одного скалярного уравнения (1),(1.1)на отрезке и в узлах сетки заменим производную ее разностной аппроксимацией.

В результате получим систему уравнений для нахождения сеточной функции:

,

,

Эта система уравнений называется разностной схемой Эйлера.

Для нахождения имеем явную формулу

(2)

Аналогично можно получить неявную схему Эйлера

, (2.1)

если с самого начала использовать в качестве разностной аппроксимации для производной выражение .

Локальной погрешностью метода называется величина

l_i =u(t_i+1) – y_i+1.

Найдем величину локальной погрешности метода Эйлера:

l_i =u(x_i+1) – y_{i+1 =} u(x_i)+h u^’(x_i) +O(h²) –y_i – hf(x_i ,y_i )= O(h²)

при условии, что u(x_i)=y_i.

Другими словами погрешность, которую допускает за один шаг метод, стартующий с точного решения.

Глобальной погрешностью   (или просто погрешностью) численного метода называют сеточную функцию со значениями ε_i =u(x_i )-y_i

в узлах.

В качестве меры абсолютной погрешности метода примем величину

E(h)=max| u(x_i )-y_i|

0≤ i≤n-1.

Можно показать - для явных одношаговых методов из того, что локальная погрешность имеет вид

,

следует

,

где и M - некоторые константы.

Таким образом, метод Эйлера является методом первого порядка точности ( р=1 относительно h).

Для нахождения решения задачи Коши с заданной точностью требуется найти такое приближенное решение, для которого величина глобальной погрешности.

Так как точное решение задачи неизвестно, погрешность оценивают с помощью правила Рунге.

Правило Рунге оценки погрешностей.

 Для практической оценки погрешности проводят вычисления с шагами h и h/2.

За оценку погрешности решения, полученного с шагом h/2, принимают величину, равную

,

где p - порядок метода.

Метод Рунге-Кутты четвертого порядка .

Для достижения более высокой точности (порядка h⁴) используют метод Рунге-Кутты четвертого порядка:

, где

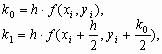(3)