Расчетно-графическая работа №2.

2.1. Интерполяционные многочлены и численное дифференцирование

Тема. Интерполяционный многочлен Лагранжа. Изучение средств системы MathCAD для построения интерполяционных многочленов.

Задание: Для заданной функциина

1. Построить интерполяционный многочлен Лагранжа для

для равноотстающих узлов.

Оценить погрешность (построить графики погрешности).

2. Используя MathCAD, выполнить интерполяцию кубическим сплайном. Оценить погрешность.

3. Для аппроксимации ,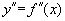использоватьисоответственно. Оценить погрешность (построить графики погрешности).

Номер варианта задания совпадает с номером студента в журнале класса.

Варианты индивидуальных заданий.

Оценить зависимость погрешности интерполяции от порядка многочлена

Номер варианта				Номер варианта
1		2	5	16		2	5
2		-9	9	17		-2	2
3		-2	2	18		-3	3
4		-1	5	19		2	5
5		-5	3	20		-3	3
6		1	3	21		-1	4
7		0	4	22		0	5
8		-5	5	23		-2	2
9		0	4	24		-2	3
10		-3	3	25		0	4
11		0	4	26		-3	3
12		0	8	27		-3	3
13		0	6	28		0	4
14		-3	2	29		-2	3
15		-4	-1	30		-2	2

 

 

2.2. Интерполяционные сплайны и приближения по методу наименьших квадратов

 

Тема. Интерполяционный кубический сплайн.

Задание: Построить интерполяционный кубический сплайн для функции , заданной таблицей, и найти его значение в указанной точке.

Найти решение той же задачи, используя встроенные функции системы MathCAD.

Сравнить полученные результаты.

Номер варианта задания совпадает с номером студента в журнале класса.

Варианты индивидуальных заданий.

 

Номер варианта	1	2	3	4	5	6	7
0.25	0.7788	1.284	0.2474	0.2526	1.031	0.2449	0.2553
0.31	0.7334	1.363	0.3051	0.3150	1.048	0.3004	0.3203
0.36	0.6977	1.433	0.3523	0.3678	1.066	0.3452	0.3764
0.39	0.6771	1.477	0.3802	0.4000	1.077	0.3714	0.4111
0.43	0.6505	1.537	0.4169	0.4434	1.094	0.4053	0.4586
0.47	0.6250	1.600	0.4529	0.4875	1.112	0.4382	0.5080
0.52	0.5945	1.682	0.4969	0.5438	1.138	0.4777	0.5726
0.56	0.5712	1.751	0.5312	0.5897	1.161	0.5080	0.6269
0.64	0.5273	1.896	0.5972	0.6846	1.212	0.5649	0.7445
0.66	0.5169	1.935	0.6131	0.7090	1.226	0.5784	0.7761
0.71	0.4916	2.034	0.6518	0.7712	1.263	0.6107	0.8595
:	0.41	0.42	0.40	0.45	0.49	0.53	0.54

 

Номер варианта	8	9	10	11	12	13	14
0.24	1.2711	0.2355	1.029	0.7866	0.2423	0.2447	0.2374
0.26	1.297	0.2544	1.034	0.7711	0.2629	0.2660	0.2571
0.27	1.310	0.2637	1.037	0.7634	0.2733	0.2768	0.2667
0.29	1.336	0.2823	1.042	0.7483	0.2941	0.2984	0.2860
0.30	1.350	0.2915	1.045	0.7408	0.3045	0.3093	0.2955
0.32	1.377	0.3097	1.052	0.7261	0.3255	0.3314	0.3146
0.37	1.448	0.3544	1.069	0.6907	0.3785	0.3879	0.3616
0.38	1.462	0.3631	1.073	0.6839	0.3892	0.3994	0.3709
0.42	1.522	0.3976	1.090	0.6570	0.4325	0.4466	0.4078
0.49	1.632	0.4556	1.122	0.6126	0.5098	0.5334	0.4706
0.59	1.804	0.5330	1.179	0.5543	0.6248	0.6696	0.5564
:	0.31	0.33	0.41	0.48	0.51	0.45	0.53

 

 

Номер варианта	15	16	17	18	19	20
1.2	0.0792	0.1823	1.063	0.3012	1.492	0.6703
1.3	0.1139	0.2624	1.091	0.2725	1.935	0.5169
1.4	0.1461	0.3365	1.119	0.2466	2.293	0.4350
1.6	0.2041	0.4700	1.170	0.2019	3.561	0.2800
1.7	0.2304	0.5306	1.193	0.1827	3.935	0.2541
1.9	0.2788	0.6419	1.239	0.1496	4.055	0.2466
2.1	0.3222	0.7419	1.281	0.1225	4.665	0.2144
2.2	0.3424	0.7885	1.301	0.1108	5.529	0.1809
2.4	0.3802	0.8755	1.339	0.0907	7.538	0.1327
2.6	0.4150	0.9555	1.375	0.0743	12.182	0.0821
2.7	0.4314	0.9933	1.392	0.0672	16.281	0.0614
:	2.3	2.0	1.8	2.5	1.61	1.39

 

Тема. Приближение функций, заданных таблицей, по методу наименьших квадратов.

Задание: Методом наименьших квадратов построить многочленов второй степени, аппроксимирующий функцию, заданную таблично. Найти значение многочлена в заданных точках, абсолютную погрешность в них и среднеквадратическую погрешность, построить графики.

Для этой же функции построить многочлен первой степени, пользуясь встроенными функциями системы MathCAD для линейной регрессии. Графически сравнить полученные результаты.

Номер варианта задания совпадает с номером студента в журнале класса.