MM - Все, что было=) / MMM / РГР_1

Индивидуальные задания по дисциплине

«Алгоритмы и вычислительные методы» .

РГР№1.

1.1. Решение алгебраических уравнений

Тема: Приближенные методы решения алгебраических уравнений. Изучение средств системы MathCAD для решения алгебраических уравнений.

Задание1: Исследование функциии решение уравнения.

Алгоритм приближенного решения уравнения состоит из двух этапов:

1. Нахождение промежутка, содержащего корень уравнения (или начальных приближений для корня), для которых выполняются достаточные условия сходимости одного из итерационных методов.

2. Получение приближенного решения с заданной точностью итерационным методом.

Первый этап алгоритма может быть реализован следующим образом:

• Задаются значения границ промежутка и количество точек .

• Вычисляется таблица значений функции на промежутке с шагом .

Строится график функции По виду графика (и по значениям функции в таблице) подбираются границы промежутка так, чтобы он содержал корень уравнения. Определяются выражения для первой и второй производной функции . Границы промежутка, содержащего корень, в случае необходимости корректируются так, чтобы на этом промежутке и были знакопостоянны.

На втором этапе должны быть использованы:

1. Средства системы MathCAD.

Следующие итерационные методы:

2. Метод хорд. (для случая f(b)*f^’’(b)>0 ).

3. Метод касательных. (для случая ).

4. Метод простых тераций.

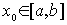
f1(x) = x - f(x)/k (для случая ).

x_k+1 = x_k – f(x_k) / k

| k | >= Q / 2

Q = max | f(x) |

Знак к совпадает со знаком f ^’(x) на [ a,b ].

Для оценки погрешности приближенного решения использовать неравенство

| x₀ – x_k | <= (M^k/(1-M))*| x₁-x₀ | ,

где M=max | f1^’(x) | на [ a,b ].А

Вычислить перечисленными выше методами изолированный корень уравнения с точностью 0.000001 .

Номер варианта задания совпадает с номером студента в журнале класса.

Варианты индивидуальных заданий.

Номер варианта		Номер варианта
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

 

1.2. Решение систем линейных алгебраических уравнений

Тема: Решение систем линейных алгебраических уравнений Ах=в. Изучение средств системы MathCAD для решения систем уравнений.

Задание:

1. Найти решение системы 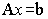средствами системы MathCAD.

2. Найти приближенное решение системы итерационными методами.

Определить количество итераций , обеспечивающих при фиксированном начальном приближении заданную точность приближенного решения. ,    Итерационные методы:

1. метод Якоби.

2. метод Зейделя;

3. метод простых итераций;

4. метод релаксации .

Решить перечисленными методами систему линейных уравнений с точностью 0.00001.

Номер варианта задания совпадает с номером студента в журнале класса.

Варианты индивидуальных заданий.

 

Матрица системы определяется формулой

,

где

k - номер варианта задания.

 

1.3. Решение алгебраической проблемы собственных значений

Тема: Вычисление собственных чисел и собственных векторов матрицы. Изучение средств системы MathCAD для вычисления собственных чисел и собственных векторов матрицы..

Задание:

1. Найти все собственные числа и собственные вектора матрицы средствами системы MathCAD с точностью 10^-4 .

2. Найти с точностью 10^-4 наибольшее по модулю собственное число заданной матрицы и соответствующий нормированный собственный вектор степенным методом (точность приближений для собственного числа определяется количеством совпадающих разрядов у соседних приближений).

3. Найти все собственные числа и собственные векора матрицы методом вращений с точностью 10^-4 .

Варианты индивидуальных заданий.

Матрица системы определяется формулой

,

где

5,342 0,599 0,432 0,202

D = 0,599 4,342 0,599 0,432

0,432 0,599 3,342 0,599

0,202 0,432 0,599 2,342

 

k - номер варианта задания. Номер варианта задания совпадает с номером студента в журнале класса.