Математические методы и модели в расчетах на ЭВМ.

Расчетно-графическая работа №1.

1.1. Решение нелинейных уравнений

Тема:Приближенные методы решения нелинейных уравнений. Изучение средств системы MathCAD для решения нелинейных уравнений.

Задание1: Решить нелинейное уравнениес заданной точностью ε.

Алгоритм приближенного решения уравнения состоит из двух этапов:

1. Найти интервал локализации , содержащий изолированный корень уравнения, в котором выполняются достаточные условия сходимости итерационных методов.

2. Получить приближенное решение с заданной точностью ε итерационными методами.

Первый этап алгоритма может быть реализован следующим образом:

• Строится график функции . По графику подбираются границы промежуткатак, чтобы он содержал изолированный корень уравнения, то естьf(a)*f(b)<0 .

• Определяются выражения для первой и второй производной функции 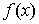и строятся их графики .

• Границы промежутка , содержащего корень, в случае необходимости корректируются так, чтобы на этом промежутке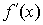и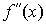были знакопостоянны.

На втором этапе должны быть использованы:

1. Средства системы MathCAD.

Следующие итерационные методы:

2. Метод хорд в форме ложного положения. - (для случаяf(b)*f ^‘’(b)>0).

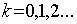
2. Метод касательных. - для случая.

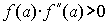2. Метод простой итерации.

x_k+1 = φ(x_k) , - в том случае , если │dφ(x)/dx < 1│ для x Є [a,b].

,

где функция φ(x) – результат разрешения уравнения относительноx, т.е.

x = φ(x) .

В случае , если │dφ(x)/dx ≥ 1│ для x Є [a,b] , то применить метод простой итерации с итерационным параметром к

x_k+1 = x_k – f(x_k) / k

| k | >= Q / 2

Q = max | df (x/)dx | - для x Є [a,b]

Знак к совпадает со знаком df (x/)dx на [a,b].

Для оценки погрешности приближенного решения использовать неравенство

| x_n+1 – x_n | < ε .

Вычислить перечисленными выше методами изолированный корень уравнения с точностью ε= 0.000001.

Номер варианта задания совпадает с номером студента в журнале класса.

Варианты индивидуальных заданий.

Номер варианта		Номер варианта
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

1.2. Решение систем линейных алгебраических уравнений

Тема: Решение систем линейных алгебраических уравненийAx=b.Изучение средств системы MathCAD для решения систем линейных алгебраических уравнений.

Задание:

1. Найти решение системы средствами системы MathCAD.

2. Найти приближенное решение системы итерационными методами.

2.1. Проверить сходимость итерационного метода.

2.2. Определить количество итераций , обеспечивающих при фиксированном начальном приближении заданную точность приближенного решения.,

  . Итерационные методы:

1. Метод Якоби.

2. Метод Зейделя;

3. Метод простых итераций;

4. Метод релаксации.

Решить перечисленными методами систему линейных уравнений с точностью = 0.0000001.

Номер варианта задания совпадает с номером студента в журнале класса.