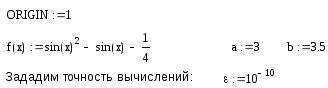2) Получение приближенного решения уравнения с заданной точностью методом бисекций

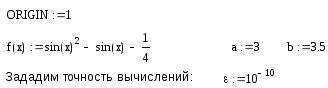
3) Получение приближенного решения уравнения с заданной точностью методом хорд

4) Получение приближенного решения уравнения с заданной точностью методом простейших итераций

5) Получение приближенного решения уравнения с заданной точностью методом касательных (Ньютона)

Аналогично методу хорд, используя материал, рассмотренный в пункте «Теоретические сведения», получить решение методом касательных.

Таблица 1

N	f(x)	[a1, b1]
1
2
3
4
5
6
7		[5,25]
8		[0.1,10]
9		[0.1,2]
10

1 К сожалению, это не всегда так. Если начальное приближение выбрано неудачно и значение производной в этой точке близко к нулю, то, вообще говоря, найденный корень может быть не ближайшим к начальному приближению.