4.Метод простейших итераций

Этот метод основан на том, что функцию f(x) представляем в виде разности двух функций:

f(x)=φ₁(x)- φ₂(x), (1**)

(например: f(x)=cos(x)-e^x=φ₁(x)- φ₂(x) => φ₁(x)=cos(x) ; φ₂(x)=e^x ).

При подстановке корня функция обращается в нуль f(x^*)=0. Тогда

φ₁(x)- φ₂(x)=0

φ₁(x)=φ₂(x) (***)

Графически представим так:

φ₁(x)

:

φ₂(x)

φ₁(x)=φ₂(x)

То есть необходимо найти значение х, при котором бы выполнялось условие (***). Пусть, например φ₁(x)=x и φ₂(x)= φ(x), тогда равенство (1**) примет вид

f(x)=x- φ(x)=0  x = φ(x) (2**)

Приблизительно в окрестности корня выбираем x₀ тогда согласно формуле (2**):

х₁= φ(x₀).

Полученное выражение x₁ отличается от x₀, то есть x₀ не равен φ(x₀).

Подставим х₁ в (2**). Аналогично φ(x₁)= x₂, но x₂ не равно x₁. Не выполнение уравнения (2**) получается из-за того, что x₀ лишь стремится к корню , но на первом шаге (k=1) мы выбирали x₀ с большой погрешностью, и оно далеко не равно корню , поэтому найденноеx₁ не корень, а лишь приближается к нему. Поэтому производим следующее уточнение: (приближение) к корню по формулам:

x_k =φ(x_k-1).

Допустим x=10 – точное значение корня. Методом итераций получаем следующие значения:

x₁ =φ(x₀)= φ(9) x₁ =9.2,

x₂ =φ(x₁)= φ(9.2) x₂ =9.283,

x₃ =φ(x₂)= φ(9.283) x₃ =9.35,

x₄ =φ(x₃)= φ(9.35) x₄ =9.64,

x₅ =φ(x₄)= φ(9.64) x₅ =9.773,

x₆ =φ(x₅)= φ(9.773) x₁ =9.848,

…………………………………

x_n = φ(x_k-1)= φ(9.99998)=9.99999.

Условие окончания итерационного процесса:

.

Итерационный процесс:

1. Выбираем x₀.

2. Строим φ(x). Для этого из точки x₀ проводим перпендикуляр на ось OX и получаем следующую точку [ x₁= φ(x₀) ].

3. Затем перпендикулярно этой точке стоим следующую

4. …

5. И т. д. до приближения к корню.

Итерационный процесс для случая, когда данная функция f(x) резко убывает (возрастает), будет расходящимся:

За скорость возрастания (убывания) функции отвечает первая производная, поэтому для применения этого метода необходимо, чтобы первая производная была малой величиной:

.

Если это условие не выполняется, тогда производятся следующие действия  вводим фиктивный параметр k.

f(x)=0

Справедливо, что если домножить правую и левую часть этого равенства на (-k), то оно не изменится:

-kf(x)=-k*0

Аналогично можно прибавит к правой и левой части х:

x-kf(x) = x,

Можно обозначить

(х) = x-kf(x)

В итоге получаем:

x_k= f(x_k-1) (3*)

Условием сходимости итерационного процесса (3*) является:

.

Обозначим

τ =1/k.

Т. о. получим итерационный процесс:

,

где τ определяется из условия:

τ >= Q

Q = {max_[a;b] [f `(x)| }/2,

Т. е.  выбирается больше либо равным половине модуля максимума производной f(x) на интервале [a;b].

Например

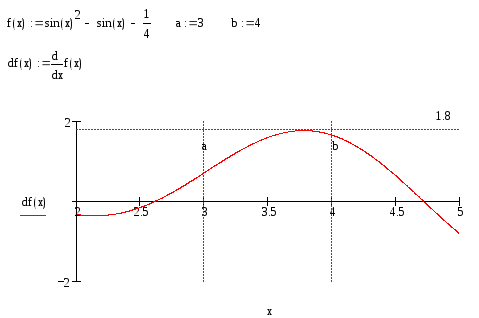
По графику видно, что максимум первой производной на интервале [a,b]

Q = |1,8| = 1,8.

Тогда  можно выбрать равным, например

 = 1.

Описание работы задание

Дано уравнение:

f(x)=0.

Найти с точностью  = 10^-10 (|x_n-x_n-1|<.) все корни уравнений, содержащиеся на отрезке [a1,b1]. Для этого использовать методы:

1. Средства системы MathCAD.

2. Численные методы:

1. Метод бисекций,

2. Метод хорд,

3. Метод касательных (метод Ньютона),

4. Метод простейших итераций.

Сравнить полученные результаты (вычислить ошибку по каждому методу eps = |Xt-x_n|):. Варианты заданий приведены в таблице 1.