
Министерство топлива и энергетики украины
МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ УКРАИНЫ
Севастопольский Национальный университет ядерной энергии и промышленности
инструктивно-методические указания
по проведению практического занятия № 9a
на тему: «КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ В СРЕДЕ MATLAB И SIMULINK »
Севастополь
«УТВЕРЖДАЮ»
Заведующий кафедрой компьютезированных систем
______________________________ Н.Сапожников
«___» _____________ 2004 г.
практическое занятие № 9а
по дисциплине «Математические методы и модели в расчетах на ЭВМ»
Время: 2 часа
Место проведения: компьютерный класс
Тема: «КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ В СРЕДЕ MATLAB И SIMULINK»
план ПРАКТИЧЕСКОГО ЗАНЯТИЯ
1. Вводная часть 05 мин.
2. Основная часть: 70 мин.
3. Выдача заданий на самостоятельную работу 05 мин
и проверка результатов выполнения контрольных
задач.
организационно-методические указания по
проведению практического занятия
Занятие проводится в составе класса в помещении компьютерного класса.
Подготовка к занятию заключается в изучении материала данного в качестве задания на самостоятельную работу и материала лекции по данной тематике.
В процессе проведения занятия обучаемым задаются контрольные вопросы с целью определения степени усвоения учебного материала.
Содержательная часть и возможные варианты исполнения приведены ниже.
1. Фигуры Лиссажу.
Начнем с очень простой задачи – построить на экране график функции, заданной параметрически :
_
x = a1 * cos(ω1t)
y = a2 * cos(ω2t)
Если отношение ω1/ω2 -число рациональное, то такая кривая называется фигурой Лиссажу.
Такие кривые можно увидеть на экране осциллографа.
Для этого создадим программу-сценарий
% Задание амплитуд и частот
a1=1.2; % Точка с запятой после оператора
a2=1.0; % обеспечивает отсутствие вывода
w1=1.5; % результата действия оператора
w2=1.0;
% Оператор задания вектора значений t
t=0:0.1:3.2;
% Вычисление векторов x, y
x=a1*cos(w1*t);
y=a2*cos(w2*t);
% Построение графика y(x)
plot(x,y);
При этом происходит автоматический подбор удобного масштаба. Масштабные метки и числа при них изображаются на границах рамки, а изображение осей координат не предусмотрено.
Получив соответствующий рисунок, мы обнаруживаем, что нарисована лишь часть кривой, во всяком случае она не имеет привычный вид фигуры Лиссажу.
Попробуем расширить диапазон вычисления и вывода кривой.
После редактирования наша программа-сценарий будет выглядеть следующим образом.
t=0:0.1:10;
x=a1*cos(w1*t);
y=a2*cos(w2*t);
plot(x,y);
Полученный в этом примере график будет иметь вид, показанный на рис. 1.

Рис. 1. Пример кривой Лиссажу.
Представляет интерес получить различные графики при различных значениях параметров.
Если вам необходимо просто нарисовать еще одну кривую с другими параметрами ,то проще всего в той же программе-сценарии присвоить им новые значения и снова повторить последовательность вычислений и вывод графика.
Такой метод работы удобен при необходимости разовых вычислений, но если вы хотите исследовать зависимость получаемой кривой от параметров, то представляет интерес научиться делать это систематически.
Задание 1. Выполните вычисление и построение фигур Лиссажу для разных отношений ω1/ω2 и для разных значений амплитуд a1 и a2.
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Второй вариант расчета фигур Лиссажу %
%%%%%%%%%%%%%%%%%%%%%%%%%%
% Задание коэффициентов
a1=1.2; a2=1.0; w2=1.0;
% Задание значений вектора t
t=0:0.1:15; x=a1*cos(w2*t);
% Задание разных частот w1
w1=1.25:0.25:2.0;
%Цикл вывода разных графиков на одном листе
for k=1:4,
y=a2*cos(w1(k)*t);
% Задание вектора-строки вывода надписей
s=[’w1/w2=’ num2str(w1(k))];
% Вывод разных графиков в разных местах листа (экрана)
% Оператор subplot задает место на листе, где
% график будет нарисован последующей командой
subplot(2,2,k); plot(x,y); title(s);
end;
Написанная выше программа-сценарий имеет несколько новых операторов :
oператор
s=[’w1/w2=’ num2str(w1(k))];
можно для большей ясности представить в виде нескольких операторов s1=’w1/w2’ – формирование вектор-строки , каждый элемент которой является символом, т.е. формирование строки текста.
oператор
s2=num2str(w1(k)) – формирование строки текста с помощью функции num2str, которая превращает числовую переменнную w1(k) в ее строковое представление.
Пусть, например, w1(1)=2.34 , тогда оператор s2=num2str(w1(1))
эквивалентен присвоению s2=’2.34’.
И последнее действие – объединение двух векторов s1 и s2 в один с помощью конструкции вида s=[s1 s2].
Таким образом можно явно задавать вектора и матрицы , причем элементами, стоящими внутри квадратных скобок, могут быть как числа или буквы, так и целые вектора и даже матрицы.
Созданная описанным образом строковая переменная s используется впоследствии в операторе title в качестве аргумента, в результате чего у каждого подрисунка появляется свой заголовок.
Новым в приведенной программе является также оператор цикла for...end и оператор subplot(m,n,k), которые позволяют на одном рисунке создать матрицу из mxn отдельных рисунков, причем параметр k определяет номер рисунка по порядку слева направо и сверху вниз.
Результат использования программы показан на рис. 2. Заметим, что в исходном тексте программы представлены фигуры Лиссажу не самого общего вида.
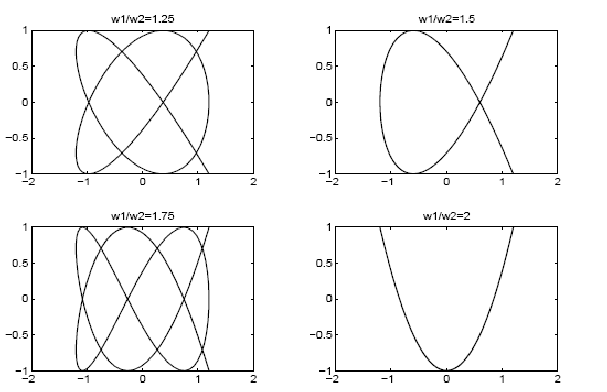
Задание 2. Включите начальные фазы ϕ1 и ϕ2 в аргументы косинусов, т.е. cos(ω1t) замените на cos(ω1t + ϕ1) и cos(ω2t) на cos(ω2t + ϕ2).
Задание 3. Еще одна модификация программы – замена процедуры plot на процедуру comet – позволит изображать «бегущий» участок кривой и анализировать, сколько раз точка пробегает кривую при изменении времени t в заданном интервале.
Задание 4. Выполните вычисление и построение фигур Лиссажу в среде Simulink для разных отношений ω1/ω2 и для разных значений амплитуд a1 и a2 в соответствии с Заданием 1 и Заданием 2 .
Порядок построения модели :
Запуск Simulink.
Для запуска программы необходимо предварительно запустить пакет MATLAB.
Основное окно пакета MATLAB показано на Рис. 1. Там же показана подсказка ,появляющаяся в окне при наведении указателя мыши на ярлык Simulink в панели инструментов.

Рис 1. Основное окно программы MATLAB.
После открытия основного окна программы MATLAB нужно запустить программу Simulink. Это можно сделать одним из трех способов:
Нажать кнопку
 (Simulink)на
панели инструментов командного окна
MATLAB.
(Simulink)на
панели инструментов командного окна
MATLAB.
В командной строке главного окна MATLAB напечатать Simulink и нажать клавишу Enter на клавиатуре.
Выполнить команду Open… в меню File и открыть файл модели (mdl - файл).
Последний вариант удобно использовать для запуска уже готовой и отлаженной модели, когда требуется лишь провести расчеты и не нужно добавлять новые блоки в модель.
Использование первого и второго способов приводит к открытию окна обозревателя разделов библиотеки Simulink (рис. 2).
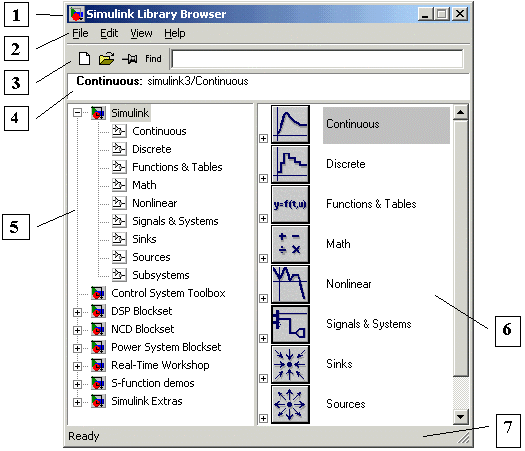
Рис 2. Окно обозревателя разделов библиотеки Simulink
Окно обозревателя библиотеки блоков содержит следующие элементы (Рис. 2):
Заголовок, с названием окна – Simulink Library Browser.
Меню, с командами File, Edit, View, Help.
Панель инструментов, с ярлыками наиболее часто используемых команд.
Окно комментария для вывода поясняющего сообщения о выбранном блоке.
Список разделов библиотеки, реализованный в виде дерева.
Окно содержимого раздела библиотеки (список вложенных разделов библиотеки или блоков)
Строка состояния, содержащая подсказку по выполняемому действию.
На рис. 2 выделена основная библиотека Simulink (в левой части окна) и показаны ее разделы (в правой части окна).
Библиотека Simulink содержит следующие основные разделы:
Continuous – линейные блоки.
Discrete – дискретные блоки.
Functions & Tables – функции и таблицы.
Math – блоки математических операций.
Nonlinear – нелинейные блоки.
Signals & Systems – сигналы и системы.
Sinks - регистрирующие устройства.
Sources — источники сигналов и воздействий.
Subsystems – блоки подсистем.
При выборе соответствующего раздела библиотеки в правой части окна отображается его содержимое (Рис. 3).

Рис 3. Окно обозревателя с набором блоков раздела библиотеки
