МИНИСТЕРСТВО ТОПЛИВА И ЭНЕРГЕТИКИ УКРАИНЫ

МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ УКРАИНЫ

Севастопольский Национальный университет ядерной энергии и промышленности

инструктивно-методические указания

по проведению практического занятия №4

на тему: «Алгебраическая проблема собственных значений»

Севастополь

Краткие сведения из теории.

Алгебраическая проблема собственных значений

Большое число научно-технических, экономических и других задач, а также потребности самой вычислительной математики приводят к вопросу нахождения собственных чисел и собственных векторов матриц, т. е. отыскание таких значений , для которых существуют решения системы алгебраических уравнений :

( 1 )

Различают две постановки задачи и самих этих решений:

- нахождение одного или нескольких собственных чисел (и соответственно - векторов) - частичная проблема собственных значений;

- нахождение всех собственных чисел (и соответственно - векторов) - полная проблема.

Среди большого числа алгоритмов, предназначенных для решения этих задач, нет такого, который можно было бы рассматривать как универсальный, пригодный во всех случаях.

1. Степенной метод

Степенной метод позволяет найти наибольшее по модулю собственное значение и собственный вектор.

Пусть  - собственные числа матрицы A. Для определенности предположим, что

Берем произвольный ненулевой вектор . Строим последовательность векторов

, ,..., 

Тогда

( 2 )

для любого номера i=1,2,...,n.

Точнее

( 3 )

Взяв достаточно большой номер итерации m, мы сможем с любой степенью точности определить по формуле (2) наибольший по модулю корень  характеристического уравнения для матрицы A. Для нахождения этого корня может быть использована любая координата  вектора , в частности, можно взять среднее арифметическое соответствующих значений.

Поскольку собственный вектор определяется с точностью до скалярного множителя, то сам вектор  приближенно представляет собой собственный вектор матрицы A, соответствующий собственному значению .

2. Метод вращений

Метод вращения позволяет для симметрических матриц решать полную проблему собственных значений.

Сущность метода состоит в следующем.

Известно, что для симметрической матрицы A существует ортогональная матрица U такая, что

( 4 )

где  - транспонированная к U матрица, а  - диагональная матрица.

Так как , то матрица  подобна матрице A и, следовательно, имеет те же собственные значения, что и матрица A.

Так как собственными значениями диагональной матрицы являются ее диагональные элементы, то зная U, мы можем найти все собственные значения матрицы A. Одновременно мы получим и все собственные векторы матрицы A, в качестве которых можно взять столбцы матрицы U.

Пусть , где  мало отличается от диагональной матрицы, т. е. элементы вне главной диагонали малы.

Тогда можно ожидать, что собственные числа матрицы  будут близки к диагональным элементам  матрицы , и  можно принять за приближенные значения .

Таким образом, решение полной проблемы собственных значений сводится для симметрической матрицы A к нахождению ортогональной матрицы U, с помощью которой матрица A приводится к диагональному виду.

В методе вращения матрица U строится как предел последовательности произведений матриц простых поворотов, при которых все оси координат кроме двух остаются неподвижными. При этом матрицы простых поворотов подбираются так, чтобы при преобразовании матрицы с помощью матрицы простого поворота на каждом шаге уничтожался максимальный по модулю недиагональный элемент.

Итерационный процесс осуществляется следующим образом.

Пусть  - матрица, полученная после k - го преобразования поворота.

В матрице  находится максимальный по модулю элемент . Строится ортогональная матрица простого поворота вида

( 5 )

Угол  подбирается так, чтобы у матрицы

( 6 )

элемент  обратился бы в нуль.

Найдем выражение для этого элемента.

Обозначим

  . ( 7 )

Матрица  отличается от матрицы  только столбцами с номерами  i и  j , причем последние имеют такой вид:

( 8 )

Матрица  отличается от матрицы  только строками с номерами i и j .

Таким образом,

a^k+1_ij ( 9 )

Из требования, что , получаем

( 10 )

Процесс заканчивается, когда все внедиагональные элементы полученной на очередном шаге матрицы  будут достаточно малы.

Диагональные элементы этой матрицы являются приближениями для собственных чисел матрицы A, а столбцы матрицы  приближениями для соответствующих собственных векторов.

Метод вращения является одним из самых удобных итерационных методов для определения собственных значений и собственных векторов симметрических матриц. Он прост по вычислительной схеме, быстро сходится, кратные и близкие собственные значения не вызывают никаких трудностей.

Вычисление собственных чисел и собственных векторов матрицы в среде MathCad.

Тема: Вычисление собственных чисел и собственных векторов матрицы методом вращения.

Пример.

В исходной матрице выше главной диагонали выбирается максимальный элемент. Определяется угол поворота.

Строится ортогональная матрица простого поворота. Угол подбирается так, чтобы у матрицы A0 элемент обратился в нуль.

Дальнейшие преобразования проводятся аналогично.

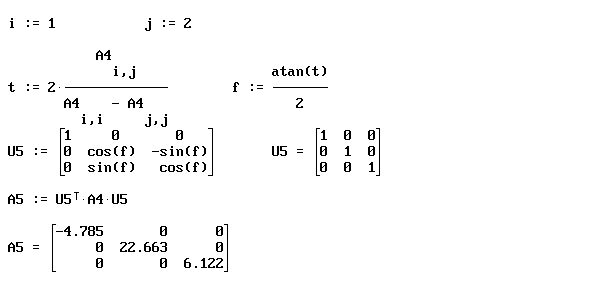
Через конечное число шагов получена матрица, на главной диагонали которой стоят собственные числа исходной матрицы.

Столбцы матрицы U являются нормированными собственными векторами исходной матрицы.

6