Варианты задания 5

№ варианта	f(x, y, y’)	Граничные условия
		a		b		y(a)	y(b)
1	ex y + cos x	1	2		0			0
2	y sin x + e -x	2	3		1			0
3	y cos x + tg x	0	1		0			0.45
4	x3 y + cos x	0	1		1			0
5	x + ex y/(1 - x)	2	4		1			0.14
6	x2 y + 1/(1 + x)	1	3		0			0.17
7	y cos x + cos 2x	1	2		0			0
8	(2 + x) y + arctg x	0	3		0			0.22
9	(5 - x) y + x	2	4		0			-1.2
10	e -x y + 2 e -x	0	1.5		2.4			0
11	e -x y/x + x	-3	-2		3			0
12	(x2 + 1/x) y + 1/x 2	2	3		0			0
13	(10 - x) y + x	-1	0		2			0
14	y/x2 + x	1	3		1.5			0
15	y ln x + 1 + x	7	8		0			0

 

Решение в Mathcad

Лабораторная работа № 6 Решение обыкновенных дифференциальных уравнений

Задание 1

Решить дифференциальное уравнение y'=2x²+2y

Начальные условия

Точное решение

Метод Эйлера

Метод Рунге-Кутта

Метод Адамса

Сравнение методов решений обыкновенных дифференциальных уравнений:

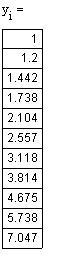
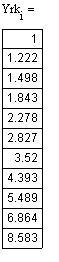
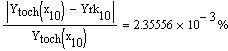
Решение средствами Mathcad

- задание начального значения

- определение функции, задающей производную

- вычисление решения в 10 промежуточных точках на отрезке [0,1]

Задание 2

Решение дифференциального уравнения второго порядка z'' = - z' +2z z(0) = 1 z'(0) = 3

<- z(0)

- Задание начальных условий

<- z'(0)

- Первая производная

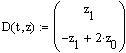
- Вторая производная

- вычисление решения в 10 промежуточных точках на отрезке [0,0,5]

Задание 3

Решение системы дифференциальных уравнений u" = 2v v'' = 4v - 2u с начальными условиями u(0) = 1.5 v(0) = 1 u'(0) =1.5 v'(0) = 1

<- u(0)

<- u'(0)

<- Определение вектора начальных условий

<- v(0)

<- v'(0)

u'

u"

<- Определение вектора первых и вторых производных

v'

v"

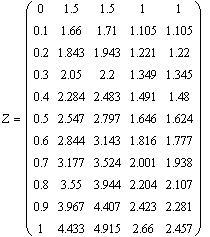
<-Вычисление решения в 10 промежуточных точках на отрезке [0,1]

Задание 4. Решение краевой задачи

Преобразование краевой задачи y'' = 2x + 3y y(0) = 0 y(1) =1 к задаче Коши

- cтартовое значение для поиска величины y'(0)

- известное у(0)

- неизвестные начальные условия. Должны быть определены с помощью sbval

- первая производная

- вторая производная

- разница между вычисленными и заданными значениями у

- y'(0) Недостающее начальное условие требуемое функцией rkfixed

РЕШЕНИЕ ЗАДАЧИ КОШИ

- Задание начальных условий

- Первая производная

- Вторая производная

- вычисление решения в 5 промежуточных точках на отрезке [0,1]
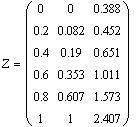