
Министерство топлива и энергетики Украины
Севастопольский национальный университет ядерной энергии и промышленности
Факультет информационных технологий
Кафедра эколого-экономического мониторинга
Расчетно-графическая работа №1
по дисциплине «Математические методы оптимизации и исследования операций»
Выполнила: ст. 642 гр
Лёгенькая Анна
Проверил:
Смычков Е. Е.
Севастополь 2010
Вычислительная работа №1
Цель работы: в ходе пройденных практический работ показать как научились решать задачи графическим методом, симплекс-методом, двойственные задачи, а также транспортные задачи.
n-номер в списке в журнале группы;
m-количество букв у фамилии,
где n=11, m=9.
Ход работы
Ι. В дневном рационе два собравшихся продукта питания Р1 и Р2 . Причем продукта Р1 должно войти не более 200 единиц. Стоимость единицы продукта Р1 составляет 20 коп, а продукта Р2 составляет (40-n) коп. Эти два продукта содержит три основные витамина A, B, C. В продукте Р1 они входят в количестве 20; 10+m; 10+n единиц; а в продукте Р2 в количестве 25; 15+n; 5+n единиц соответственно.
Определить оптимальный рацион с минимальной стоимостью, если витамину А в рационе должно быть не меньше 120 единиц, витамина B – 80 единиц; витамина С – 200 единиц.
Решение:
-
Составить таблицу с данными:
|
|
P1 |
P2 |
количество |
|
A |
20 |
25 |
120 |
|
B |
19 |
26 |
80 |
|
C |
21 |
16 |
200 |
|
стоимость |
20 |
29 |
|
|
|
x1 |
x2 |
|
-
Данная задача является на min, следовательно составляем систему:
z=20*x1+29*x2→min


-
Запишем данную систему в виде ограничений:

-
Разделим коэффициенты при x1 и x2 так, чтобы после знака “=” стояла 1. То есть запишем уравнение в отрезках:

grad z=(20;29)
После того как построили прямые в отрезках, построили градиент, подставили перпендикуляр к градиенту.
Находим Xmin=
Оптимальным рационом с минимальной стоимостью является наличие продукта питания ( ) в количестве единиц и стоимостью денежных единиц.
ΙΙ. Предприятие может выпускать 4 вида продукции П1, П2, П3, П4. Для их выпуска используется 3 вида ресурсов. Общий объем ресурсов соответственно составляет 100m; 100m(m+3); 90m+50 единиц. Нормы затрат этих ресурсов на изготовление единицы продукции каждого вида приведено в таблице. Цена реализации продукции П1 составляет 2 – m; П2 составляет 3m; П3 составляет 2m+5; П4 составляет 3m-2.
-
Найти план выпуска продукции, который дает максимальную выручку;
-
Составить модель двойственной задачи. Найти решение двойственной задачи;
-
Дать экономический анализ основных и дополнительных переменных обеих задач.
Решение:
-
Составим таблицу к данной задаче:
|
|
П1 |
П2 |
П3 |
П4 |
объём |
|
1 |
11 |
6 |
9 |
11 |
900 |
|
2 |
22 |
33 |
13 |
21 |
1200 |
|
3 |
5 |
22 |
11 |
9 |
860 |
|
цена |
18 |
27 |
23 |
25 |
|
-
Составим систему:
max z=18*x1+27*x2+23*x3+25*x4
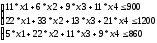
-
Добавляя базисные переменные, приводим к каноническому виду:

4.

5. Решаем задачу симплекс-методом:
|
БП |
Сб |
Ао |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
18 |
27 |
23 |
25 |
0 |
0 |
0 |
|||
|
x5 |
0 |
900 |
11 |
6 |
9 |
11 |
1 |
0 |
0 |
|
x6 |
0 |
1200 |
22 |
[33] |
13 |
21 |
0 |
1 |
0 |
|
x7 |
0 |
860 |
5 |
22 |
11 |
9 |
0 |
0 |
1 |
|
Zj-Cj |
0 |
-18 |
-27 |
-23 |
-25 |
0 |
0 |
0 |
|
Самое наименьшее отрицательное число -27, а разрешающий элемент 33.
|
БП |
Сб |
Ао |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
||||||
|
18 |
27 |
23 |
25 |
0 |
0 |
0 |
|||||||||
|
x5 |
0 |
7500/11 |
7 |
0 |
73/11 |
79/11 |
1 |
-2/11 |
0 |
||||||
|
x2 |
27 |
400/11 |
2/3 |
1 |
13/33 |
7/11 |
0 |
1/33 |
0 |
||||||
|
x7 |
0 |
60 |
-29/3 |
0 |
7/3 |
-5 |
0 |
-2/3 |
1 |
||||||
|
Zj-Cj |
10800/11 |
0 |
0 |
136/11 |
-86/11 |
0 |
9/11 |
0 |
|||||||
|
БП |
Сб |
Ао |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
18 |
27 |
23 |
25 |
0 |
0 |
0 |
|||
|
x5 |
0 |
39360/77 |
2656/77 |
0 |
0 |
1648/77 |
1 |
-219/77 |
-219/77 |
|
x2 |
27 |
2020/77 |
177/77 |
1 |
0 |
114/77 |
0 |
-13/77 |
-13/77 |
|
x3 |
23 |
180/7 |
-29/7 |
0 |
1 |
-15/7 |
0 |
3/7 |
3/7 |
|
Zj-Cj |
100080/77 |
-3944/77 |
0 |
0 |
-2642/77 |
0 |
-19/7 |
408/77 |
|
|
БП |
Сб |
Ао |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
|
18 |
27 |
23 |
25 |
0 |
0 |
0 |
||||
|
x5 |
0 |
20800/177 |
0 |
-2656/177 |
0 |
-48/59 |
1 |
-76/177 |
-55/177 |
|
|
x1 |
18 |
2020/177 |
1 |
77/177 |
0 |
38/59 |
0 |
11/177 |
-13/177 |
|
|
x3 |
23 |
12920/177 |
0 |
319/177 |
1 |
31/59 |
0 |
-5/177 |
22/177 |
|
|
Zj-Cj |
333520/177 |
0 |
3944/177 |
0 |
-78/59 |
0 |
83/177 |
272/177 |
||
|
БП |
Сб |
Ао |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
|
18 |
27 |
23 |
25 |
0 |
0 |
0 |
||||
|
x5 |
0 |
7520/57 |
24/19 |
|
0 |
0 |
1 |
|
|
|
|
x4 |
25 |
1010/57 |
59/38 |
|
0 |
1 |
0 |
|
|
|
|
x3 |
23 |
1210/19 |
-31/38 |
|
1 |
0 |
0 |
|
|
|
|
Zj-Cj |
108740/57 |
39/19 |
1321/57 |
0 |
0 |
0 |
34/57 |
79/57 |
||
Подставляем найденные x в целевую функцию:
max z=18*0+27*0+23*108740/57+25*1010/57
max z=108740/57
6. Составляем двойственную систему:
min F=900*x1+1200*x2+860*x3

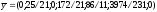
min F=900*0+1200*25/21+860*0
min F=10000/7
Согласно решению, чтобы получить прибыль 10000/7 тыс. у.е. нужно выпускать 400/7 ед. продукта П3 ,продукты П1 , П2 ,П4 выпускать не рентабельно.
Переменная x7 =2420/7 означает что, четвертый ресурс используется не полностью, имеется остаток в количестве 2420/7.
Двойственные переменные показывают меру дефицитности ресурсов. Они численно равны изменению целевой функции при изменении соответствующего ресурса на единицу. Изменении второго ресурса на единицу приводит к увеличению обьема реализации на 25/21 денежных единиц. Дополнительные двойственные переменные показывают меру убыточности продукции, которую согласно решению нецелесообразно выпускать.
ΙΙΙ. Решить транспортную задачу.
|
|
50 |
90 |
81 |
70 |
80 |
9 |
|
100 |
11 |
10 |
9 |
11 |
4 |
8 |
|
20 |
7 |
7 |
1 |
2 |
5 |
9 |
|
80 |
11 |
12 |
11 |
3 |
8 |
8 |
|
15 |
9 |
10 |
1 |
6 |
10 |
10 |
|
2 |
11 |
9 |
8 |
5 |
4 |
3 |
-
Решаем методом с-з:
Проверяем
 и
и
 ,
,
 =217,
а
=217,
а
 =380,
следовательно добавляем к
=380,
следовательно добавляем к
A недостающую сумму в размере 163 и причем оценки равны 0.
|
|
50 |
90 |
81 |
70 |
80 |
9 |
|
100 |
11 50 |
10 50 |
9
|
11
|
4
|
8
|
|
20 |
7
|
7 20 |
1
|
2
|
5
|
9
|
|
80 |
11
|
12 20 |
11 60 |
3 17 |
8
|
8
|
|
15 |
9
|
10
|
1 15 |
6 15 |
10
|
10
|
|
2 |
11
|
9
|
8 2 |
5 2 |
4
|
3
|
|
163 |
0
|
0
|
0 4 |
0 70 |
0 80 |
0 9 |
L=50*11+10*50+7*20+12*20+11*60+15*1+8*2+4*0+0*70+0*80+0*90=2121(ден. единиц)
-
Решаем методом наименьшего элемента:
|
|
50 |
90 |
81 |
70 |
80 |
9 |
|
100 |
11
|
10
|
9 20 |
11
|
4 80 |
8
|
|
20 |
7
|
7
|
1 20 |
2
|
5
|
9
|
|
80 |
11 3 |
12
|
11
|
3 70 |
8
|
8 7 |
|
15 |
9
|
10
|
1 15 |
6
|
10
|
10
|
|
2 |
11
|
9
|
8
|
5
|
4
|
3 2 |
|
163 |
0 47 |
0 90 |
0 26 |
0
|
0
|
0
|
L=13*9+80*4+7*8+20*1+10*10+70*3+15*1+2*3=840(ден. единиц)
