
- •Чевын м.А.
- •1.7. Формулы Крамера:
- •Раздел II: элементы векторной алгебры.
- •Раздел III: аналитическая геометрия.
- •3.9. Плоскость в пространстве:
- •Раздел VI: уравнения и графики кривых в полярной системе координат.
- •Раздел VII: кривые, заданные параметрически.
- •Раздел VIII: нахождение пределов.
- •8.1. Определение пределов:
- •8.2. Бмф и ббф:
- •8.3. Алгоритм нахождения пределов от алгебраических функций:
- •9.2. Таблица производных:
- •9.3. Логарифмическое дифференцирование:
- •9.4. Дифференцирование функций, заданных неявно:
- •9.5. Дифференцирование функций, заданных параметрически:
- •9.6. Производные высших порядков:
- •9.7. Раскрытие неопределенностей по правилу Лопиталя:
- •9.8. Формула Тейлора:
- •9.10. Общая схема исследования функции и построения ее графика:
- •Раздел X: комплексные числа.
- •10.2. Действия над комплексными числами:
- •Раздел XI: неопределенный интеграл.
- •11.1. Определение и свойства:
- •1.2 Таблица дифференциалов и интегралов:
- •11.3 Общие методы интегрирования:
- •Раздел XII: определенный интеграл.
- •12.1. Определение и свойства:
- •12.2. Методы вычисления определенного интеграла:
- •12.3. Несобственные интегралы:
- •12.4 Применения определенного интеграла:
- •Раздел XIII: дифференциальное исчисление функций нескольких переменных.
- •13.1. Основные понятия:
- •13.2. Частные производные:
- •13.3. Дифференцирование сложных функций:
- •13.4. Дифференцирование неявных функций:
- •13.5. Касательная плоскость и нормаль к поверхности:
- •13.6. Экстремумы функции двух переменных:
- •Раздел XIV: кратные интегралы.
- •14.1. Определение и свойства двойного интеграла:
- •14.3. Применения двойного интеграла:
- •14.4. Определение и вычисление тройного интеграла:
- •14.5. Применения тройного интеграла:
- •Раздел XV: криволиненйные интегралы.
- •15.4 Криволинейный интеграл по координатам:
- •15.5 Вычисление криволинейных интегралов по координатам:
- •15.6 Применения криволинейных интегралов по координатам:
- •Раздел XVI: поверхностные интегралы.
- •16.1. Определение и свойства поверхностого интеграла по площади поверхности:
- •16.4. Определение и свойства поверхностного интеграла по координатам :
- •16.5. Вычисление поверхностных интегралов по координатам:
- •Раздел I: обыкновенные дифференциальные уравнения первого порядка.
- •1.1. Основные понятия:
- •1.3. Дифференциальные уравнения высших порядков:
- •1.4.Системы диффереренциальных уравнений.
- •Раздел II: теория поля.
- •2.2. Векторное поле и его характеристики:
- •Раздел III: ряды.
- •3.3. Знакопеременные ряды:
- •3.4. Степенные ряды:
- •3.5. Ряд Тейлора:
- •3.6. Разложение элементарных функций в ряд по степеням :
- •Раздел IV: теория функций комплексного переменного.
- •4.1. Основные понятия:
- •4.2. Основные элементарные функции:
- •4.3. Определение и свойства контурного интеграла по кривой:
- •4.4. Вычисление контурных интегралов от непрерывной функции комплексного переменного:
- •4.5. Ряды Тейлора и Лорана:
- •4.7. Вычеты:
- •Раздел V:операционное исчисление.
- •5.2. Свойства преобразований Лапласа:
- •5.3. Свертка функций:
- •5.4. Теоремы разложения:
- •5.5 Таблица оригиналов и изображений:
- •Раздел VI: основы теории вероятностей.
- •6.1. Элементы комбинаторики:
- •6.2. Основные понятия теории вероянтостей:
- •6.4. Случайные величины:
- •6.4. Числовые характеристики случайных величин:
- •3) Среднее квадратическое отклонение:
6.2. Основные понятия теории вероянтостей:
Изначальные понятия: событие и вероятность.
Под событиемпонимают всякий факт, относительно которого уместно говорить: произойдет оно или нет.
События делят на: случайные, достоверные и невозможные.
Определение:
Случайнымсобытием называют всякое явление, которое в результате ОКУ может произойти или не произойти.
Обозначение:
![]()
Определение:
Событие называется достоверным, если оно заведомо происходит при ОКУ.
Обозначение:
![]() .
.
Определение:
Событие называется невозможным, если оно заведомо не происходит при ОКУ.
Обозначение:
![]()
Определение:
Несколько событий называются равновозможными, если ни одно из них не является объективно более возможным, чем любое другое.
Определение:
Несколько событий называются несовместными, если появление одного из них исключает появление любого другого и совместными, если не исключает.
Определение:
Несколько событий образуют полную группу, если в результате ОКУ обязательно происходит хотя бы одно из данных событий.
Определение (классическое определение вероятностей):
Если в результате ОКУ всевозможные
исходы составляют полную группу
![]() и равновозможных и несовместных случаев,
из которых
и равновозможных и несовместных случаев,
из которых![]() благоприятствуют появлению события
благоприятствуют появлению события![]() ,
то вероятность этого события равна
отношению числа благоприятствующих
событий к их общему числу.
,
то вероятность этого события равна
отношению числа благоприятствующих
событий к их общему числу.
Т.о.
![]() .
.
Определение:
Два события
![]() называютсяпротивоположными, если
в результате ОКУ обязательно происходит
одно и только одно из них.
называютсяпротивоположными, если
в результате ОКУ обязательно происходит
одно и только одно из них.
Теорема:![]() .
.
6.3. Теоремы сложения и умножения:
Определение:
Произведениемдвух событий называется событие, состоящее в их одновременном появлении.
Обозначение:
![]()
![]() .
.
Определение:
Два события
![]() называютсянезависимыми, если
вероятность любого из них не зависит
от того, произошло или не произошло
другое событие и зависимыми, если
зависит.
называютсянезависимыми, если
вероятность любого из них не зависит
от того, произошло или не произошло
другое событие и зависимыми, если
зависит.
Определение:
Вероятность события
![]() ,
вычисленная при условии, что событие
,
вычисленная при условии, что событие![]() произошло, называетсяусловной
вероятностьюсобытия
произошло, называетсяусловной
вероятностьюсобытия![]() .
.
Обозначение:
![]() или
или![]() .
.
Определение:
Вероятность события
![]() ,
вычисленная без учета появления, или
не появления
,
вычисленная без учета появления, или
не появления![]() называетсябезусловной вероятностьюсобытия
называетсябезусловной вероятностьюсобытия![]() .
.
Обозначение:
![]() .
.
Теорема умножения:
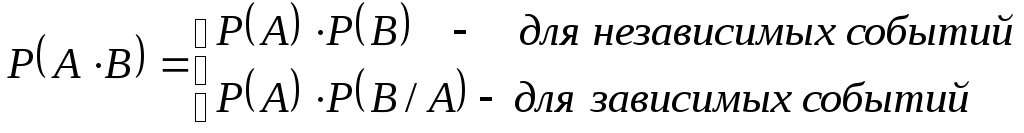
Замечание: теорема остается справедливой и для большего количества событий.
Определение:
Суммойдвух событий![]() и
и![]() называется событие, состоящее в том,
что появится хотя бы одно из этих событий.
называется событие, состоящее в том,
что появится хотя бы одно из этих событий.
Обозначение:
![]()
![]() .
.
Теорема сложения:
 .
.
Замечание: теорема остается справедливой и для большего количества событий.
Следствия:
- Сумма вероятностей несовместных
событий, образующих полную группу, равна
единице, т.е.
![]() ;
;
-
![]() - формула расчета вероятности появления
хотя бы одного из
- формула расчета вероятности появления
хотя бы одного из![]() совместных событий.
совместных событий.
Теорема (формула полной вероятности):
Если случайные гипотезы
![]() образуют полную группу несовместных
событий и событие
образуют полную группу несовместных
событий и событие![]() может
произойти только после наступления
одной из гипотез, то вероятность появления
события
может
произойти только после наступления
одной из гипотез, то вероятность появления
события![]() рассчитывается по формуле
рассчитывается по формуле
![]() .
.
Теорема (гипотез или формула Бейеса):
Пусть случайные гипотезы
![]() образуют
полную группу несовместных событий,
известны вероятности появления этих
гипотез
образуют
полную группу несовместных событий,
известны вероятности появления этих
гипотез![]() ,
событие
,
событие![]() уже произошлою, то
уже произошлою, то .
.
Повторение испытаний:
- Если
![]() ,
то
,
то![]() ;
;
- В
![]() независимых испытаниях событие
независимых испытаниях событие![]() появится хотя бы один раз с вероятностью
появится хотя бы один раз с вероятностью![]() .
.
Теорема (формула Бернулли):
Если проводится
![]() независимых испытаний, в результате
каждого из которых событие
независимых испытаний, в результате
каждого из которых событие![]() может появится с вероятностью
может появится с вероятностью![]() и не появится с вероятностью
и не появится с вероятностью![]() ,то вероятность того, что в
,то вероятность того, что в![]() испытаниях событие
испытаниях событие![]() появится ровно
появится ровно![]() раз рассчитывается по формуле
раз рассчитывается по формуле
![]()
Эта формула целесообразна при небольших
![]() .
.
Теорема (локальная теорема Муавра-Лапласа):
Если вероятность
![]() появления
события
появления
события![]() в результате каждого из
в результате каждого из![]() независимых испытаний постоянна и
отлична от 0 и 1, то при достаточно больших
независимых испытаний постоянна и
отлична от 0 и 1, то при достаточно больших![]() вероятность того, что в
вероятность того, что в![]() испытаниях событие
испытаниях событие![]() появится ровно
появится ровно![]() раз имеет представление
раз имеет представление
![]() ,
где
,
где![]() .
.
Функция
![]() - непрерывная и положительная при любых
- непрерывная и положительная при любых![]() ,
четная и
,
четная и![]() .
.
![]() .
.
При
![]() полагают
полагают![]() .
.
Закон Пуассона:
Если
![]() достаточно велико,
достаточно велико,![]() -
достаточно мало, то с наименьшей
погрешностью
-
достаточно мало, то с наименьшей
погрешностью
![]() ,
где
,
где![]() .
.
Интегральная теорема Лапласа:
Если вероятность
![]() появления события
появления события![]() в результате каждого из
в результате каждого из![]() независимых испытаний постоянна и
отлична от нуля и единицы, то при
достатолчно больших
независимых испытаний постоянна и
отлична от нуля и единицы, то при
достатолчно больших![]() вероятность
того, что событие
вероятность
того, что событие![]() наступит от
наступит от![]() до
до![]() раз имеет слудующее представление
раз имеет слудующее представление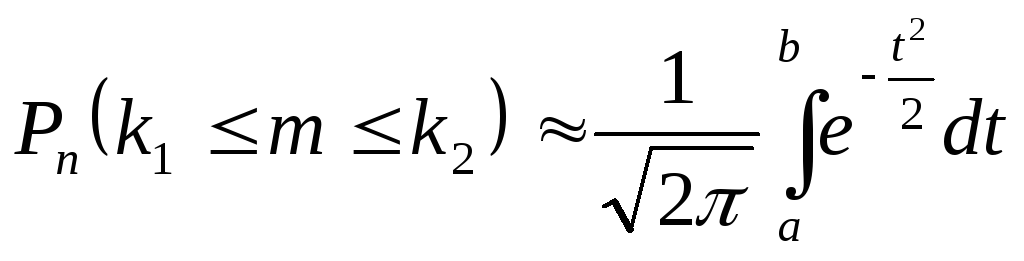 ,
где
,
где![]() ;
;![]() .
.
 - функция Лапласа.
- функция Лапласа.
![]() - непрерывна при любых
- непрерывна при любых![]() ,
нечетная
,
нечетная![]() .
.
При
![]() полагают
полагают![]() .
.
![]() .
.
