4.4. Вычисление контурных интегралов от непрерывной функции комплексного переменного:

Для неаналитических

1. ;

2. В частности, если - окружность или любая его часть, то подставивв показательной форме, имеем, что на окружности,()

, где отрезокотвечает заданной части окружности.

Замечание:формулыимеют место только для однозначных или отдельных ветвей многозначных функций.

Для аналитических

3. Теорема Коши(для односвязной области):

Если функция аналитическая в каждой точке областии на ее границе, то.

Теорема Коши(для многосвязной области):

Если функция аналитическая в многосвязной области, границей которой служат кривые, то(все границы области обходятся в одном направлении)

4. ;

5. Контурный интеграл от аналитической функции не зависит от формы кривой интегрирования, но зависит от начальной и конечнойточек пути, т.е..

6. Используя интегральную формулу Коши, имеем:

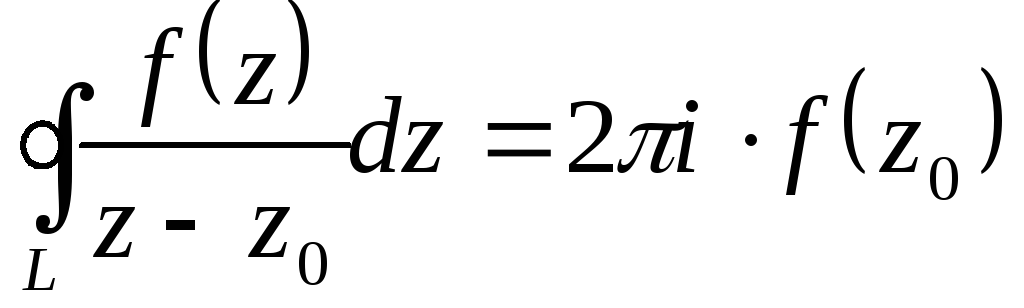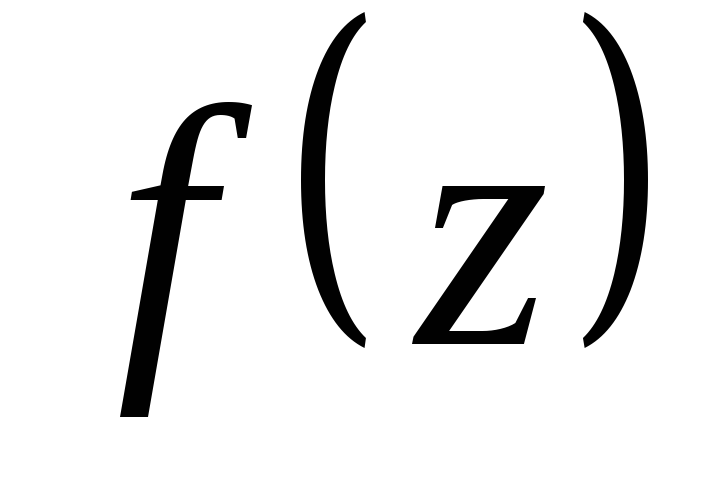• , где- аналитическая в односвязной областии на ее границе

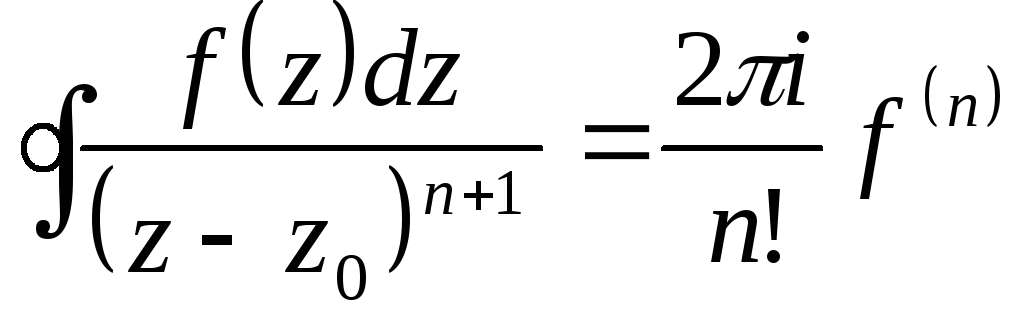• , где- аналитическая

7.

8. Теорема:

Если функция аналитическая в каждой точке области, ограниченной контуром, за исключением конечного числа изолированных особых точек, лежащих строго внутри области, то справедливо равентство:

.

4.5. Ряды Тейлора и Лорана:

Определение:

Степенной ряд , коэффициенты которого рассчитываются по формулам

называется рядом Тейлора функции, где- произвольный замкнутый контур, содержащий строго внутри точку.

Определение:

Функциональный ряд вида, где

и

называется рядом Лорана функции или компактная форма

, где

Ряд Лорана состоит из двух частей:

• -правильная

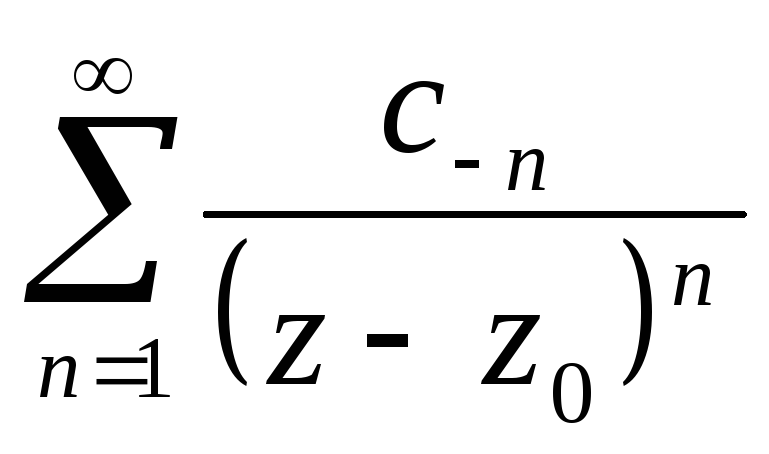• -главная часть.

6. Типы особых точек:

Определение:

Точка называется- кратным нулемфункции, если в разложении Тейлора этой функции в окрестности т.первых коэффициентов равны нулю:, но.

Определение:

Особая точка называетсяизолированной, если существует достаточно малая окрестность этой точки, не содержащая других особых точек данной функции.

Определение:

Точка называетсяособойточкой функции, если в этой точке функция не аналитическая.

Определение:

Точка называетсяустранимой особойточкой, если разложение Лорана этой функции в окрестности этой точки не содержит отрицательных степеней, т.е.

Определение:

Точка называетсяполюсом , если разложение Лорана этой функции имеет конечное число отрицательных степеней, т.е.

.

Если , то-кратный полюс, если, то простой.

Определение:

Точка называетсясущественно особойточкой, если разложение Лорана этой функции содержит бесчисленное множество отрицательных степеней, т.е.

.

Теорема:

- - кратный нуль функцииявляется- кратным полюсом функции;

- - кратный полюс функцииявляется- кратным нулем функции.

Алгоритм определения типа особой точки:

1. Применить теорему о связи между нулями и полюсами функций;

или

2. Вычислить ;

или

3. Воспользоваться определением.