Раздел II: теория поля.

1. Скалярное поле и его характеристики:

Определение:все пространство или любая его часть, в каждой точке которой задана некоторая скалярная величина, называется скалярным полем.

Характеристики скалярного поля:

1) Поверхности уровня:; линии уровня:.

2) Производная по направлению.

Формула вычисления: , где- углы,

образованные направлением дифференцирования с соответствующими

координатными осями.

Производная характеризует скорость изменения функции поля в заданном

направлении.

3) Градиент:

Формула вычисления: ;

Свойства градиета:

- направлен по нормали к поверхности уровня;

- определяет направление, по которому достигает наибольшего значения и, следовательно, функция полярастет быстрее всего.

2.2. Векторное поле и его характеристики:

Определение:

Все пространство или любая его часть, в каждой точке которой задана некоторая векторная физическая величина , называется векторным полем.

Векторное поле считается заданным, если задан вектор .

Характеристики векторного поля

1) Векторные линии:

- система дифференциальных уравнений векторных линий;

2) Поток:

и в частности , ;

В поле скоростей текущей жидкости поток вектора поля через поверхность

определяетколичество жидкости, протекающей через эту поверхность в единицу времени – физический смысл потока через незамкнутую поверхность.

В поле скоростей текущей жидкости поток вектора поля изнутри поверхности

определяетразность между количеством жидкости вытекающей и втекающей в

область в единицу времени - физический смысл потока через замкнутую поверхность.

3) Дивергенция:.

Если , то поле называется соленоидальным.

Физический смысл дивергенции:

В поле скоростей текущей жидкости дивергенция векторного поля в точке характеризует мощность источника или стока, находящегося в этой точке.

4) Циркуляция:, также по формуле:

.

Физический смысл: циркуляция силового поля вдоль замкнутого контура, помещенного в поле, выражает работу этого поля при перемещении материальной точки вдоль замкнутого контура.

5)Ротор:.

Физический смысл: в поле скоростей вращающейся жидкости ротор поля с точностью до числового множителя равен угловой скорости.

Если , то поле потенциальное.

Потенциалнаходим по формуле:

, здесь- координаты произвольной фиксированной точки поля,- координаты переменной точки поля.

Если ,, то поле называетсягармоническим.

Раздел III: ряды.

3.1. Основные понятия:

Определение:

Выражение вида называется числовым рядом.

Признаки числового ряда: наличие при суммировании бесчисленного множества членов и наличие закона изменения членов ряда.

- частичные суммы.

Определение:

Ряд называется сходящимся при, если существует конечный предел его частичных сумм и расходящимся, если такой предел не существует.

Конечный предел частичных сумм называется суммой ряда.

Теорема(необходимый признак сходимости):

Если ряд сходится, то его общий член стремится к нулю при неограниченном увеличении порядкового номера, т.е. .

Теорема(достаточный признак расходимости):

Если общий член ряда не стремится к нулю, то ряд расходится, т.е. если , то ряд

- расходится.

2. Знакопостоянные ряды:

Определение:

Ряд, все члены которого или только положительные, или только отрицательные, называется знакопостоянным.

Достаточные признаки сходимости знакоположительных рядов.

Теорема 1:

Если все члены данного знакоположительного ряда не превосходят соответствующих членов сходящегося знакоположительного ряда, то данный ряд сходится.

Теорема 2:

Если все члены данного знакоположительного ряда не меньше соответствующих членов расходищегося знакоположительного ряда, то данный ряд расходится.

Теорема 3(предельный признак сравнения):

Если существует конечный и отличный от нуля предел отношения общих членов двух знакоположительных рядов , то оба ряда одновременно либо сходятся, либо расходятся.

Ряды сравнения:

1) - геометрическая прогрессия;

2) - гармонический, расходящийся;

3) - обобщенный гармонический.

Таблица степени роста при

1.

2.

3.

4. ,- рациональное

5.

Признак Даламбера.

Целесообразно применять, когда общий член ряда содержит слагаемым или множителем хотя бы одно из выражений ,.

.

Радикальный признак Коши.

Целесообразно применять, когда общий член ряда целиком является - ой, или- ой, илистепенью какого-либо выражения.

;

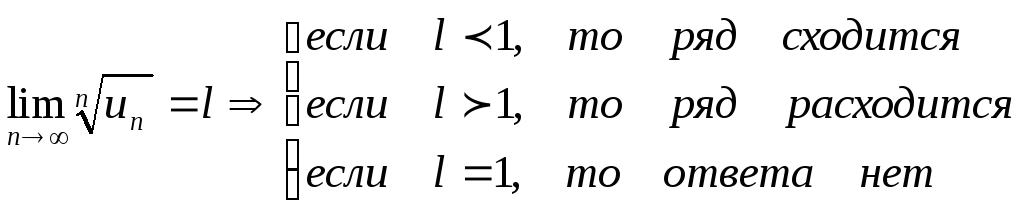Интегральный признак Коши.

Целесообразно применять, когда общий член ряда порождает функцию, первообразная которой находится без особого труда.

Если - непрерывная, положительная, убывающая в, значения которой при натуральных значениях аргументасовпадают с соответствующими значениями ряда

, то этот ряд и несобственный интегралодновременно сходятся или расходятся.

Исследование знакопостоянных рядов:

- проверить необходимое условие;

- применить признак Даламбера, радикальный признак Коши, интегральный признак Коши или признаки сравнения.