
- •Предисловие
- •1. Уравнение состояния идеального газа Пример типовой задачи
- •Решение
- •Решение
- •Варианты задач
- •2. Основное уравнение молекулярно - кинетической теории газов (уравнение клаузиуса) Пример типовой задачи
- •Исходные данные
- •3. Распределение молекул по энергиям Примеры типовых задач
- •Решение
- •Решение
- •Исходные данные
- •4. Явления переноса Пример типовой задачи
- •5. Первое начало термодинамики и его применение к изопроцессам Пример типовой задачи
- •Исходные данные
- •6. Адиабатный процесс Пример типовой задачи
- •Произведем вычисления:
- •Исходные данные
- •Второе начало термодинамики Пример типовой задачи
- •Решение
- •Исходные данные
- •Основные физические постоянные
- •Международная система измерения (система си)
- •Некоторые приставки для преобразования внесистемных единиц в систему си
- •Эффективный диаметр молекул газов (нм)
- •Периодическая таблица д.И. Менделеева
- •Литература
- •Владимир Васильевич Довгаленко
Второе начало термодинамики Пример типовой задачи
Задача
1. Один моль
идеального двухатомного газа, занимающий
объем
![]() = 12,3 л под давлением
= 12,3 л под давлением![]() = 2 атм, нагревается при постоянном объеме
до
= 2 атм, нагревается при постоянном объеме
до![]() = 3 атм. Затем газ расширяется при
постоянном давлении до
= 3 атм. Затем газ расширяется при
постоянном давлении до![]() = 24,6 л, после чего охлаждается при
постоянном объеме до начального давления
и, наконец, сжимается при постоянном
давлении до начального объема. Определить:
1) температуру точек цикла; 2) термический
коэффициент полезного действия цикла.
= 24,6 л, после чего охлаждается при
постоянном объеме до начального давления
и, наконец, сжимается при постоянном
давлении до начального объема. Определить:
1) температуру точек цикла; 2) термический
коэффициент полезного действия цикла.
Д
 ано:
ано:
= 1 моль
![]() =
12,3 л = 1,23
=
12,3 л = 1,23![]() м3
м3
![]() =
2 атм = 2
=
2 атм = 2![]() Па
Па
![]() =
3 атм = 3
=
3 атм = 3![]() Па
Па
![]() =
24,6 л = 2,46
=
24,6 л = 2,46![]() м3
м3
R
= 8,31
![]()
![]()

Перед решением задачи необходимо:
1) начертить график цикла в координатах р,V;
2) на графике отметить параметры состояния газа в каждой точке; выделить известные параметры.
Решение
Из анализа условий задачи видно, что в каждой из точек 1, 2, 3, 4 температура может быть определена из уравнения состояния газа.
Но рациональнее пользоваться уравнениями соответствующих процессов.
1)
![]()
Подставляя данные, получаем
![]() К
= 290 К;
К
= 290 К;
![]() = 290 К.
= 290 К.
2)
Процесс 1 - 2,
![]() = сonst
– изохорный.
= сonst
– изохорный.
![]()
![]() К
= 435 К;
К
= 435 К;
![]() = 435 К.
= 435 К.
3)
2 - 3 – процесс изобарный,
![]() = сonst.
= сonst.
![]()
![]() К
= 870 К;
К
= 870 К;
![]() = 870 К.
= 870 К.
4)
Процесс 3 - 4 изохорное охлаждение,
![]() =const.
=const.
![]() К
= 580 К;
К
= 580 К;
![]() К.
К.
5) Коэффициент полезного действия цикла
![]()
где
А
– работа совершенная в цикле,
![]() – количество теплоты, полученное рабочим
телом от нагревателя.
– количество теплоты, полученное рабочим
телом от нагревателя.
Полная работа, совершенная в данном цикле, равна
![]() .
.
Работы
![]() и
и![]() равны нулю, так как в изохорном процессе
изменение объемаdV
= 0, следовательно, и работа равна 0
(перемещения тел нет).
равны нулю, так как в изохорном процессе
изменение объемаdV
= 0, следовательно, и работа равна 0
(перемещения тел нет).
Полезная работа за цикл равна
![]() .
.
В изобарном процессе работа равна А = р V, следовательно,
![]()
Так
как
![]() ,
то
,
то![]()
Тогда
![]()
Полезная работа цикла численно равна площади цикла.
![]() количество
теплоты, полученное в цикле при изохорном
и изобарном нагревании, т. е. в процессах
1 - 2 и 2 - 3:
количество
теплоты, полученное в цикле при изохорном
и изобарном нагревании, т. е. в процессах
1 - 2 и 2 - 3:
![]()

КПД цикла

Вычисляем , подставив данные:
![]() ;
= 7,8 %.
;
= 7,8 %.
6) Можно сравнить КПД данного цикла с КПД обратимого цикла Карно:
![]() .
.
7) Изобразите данный цикл в координатах р,Т и V,Т:


8) Изобразите данный цикл в координатах Т, S

Ответ: Т1 = 290 К, Т2 = 435 К, Т3 = 870 К, Т4 = 580 К, = 7,8 %; графики на рисунках.
Задача 2. 6,6 г водорода расширяются изобарно до удвоения объема. Найти изменение энтропии при этом расширении.
Д ано:Решение
ано:Решение
р
Изменение
энтропии газа при переходе из одного
состояния в другое определяется только
параметрами этих состояний и не зависит
от характера процесса:
![]() .
.
т
= 6,6
![]() кг
кг
=
2
![]()
![]()
![]()
 S
- ?
S
- ?
![]() ,
,
![]() -
изобарная молярная теплоемкость,
-
изобарная молярная теплоемкость,
i = 5 количество степеней свободы для двухатомного водорода.
Тогда
![]()
![]()
Интегрируя, получаем

Для изобарного процесса
![]()
Тогда
![]()
По условию
![]()
Вычислим S:
![]()
![]() .
.
Вывод.
Энтропия при изобарном расширении
водорода увеличилась
![]() ,
следовательно, процесс необратим,
самопроизвольно сжиматься газ не может.
,
следовательно, процесс необратим,
самопроизвольно сжиматься газ не может.
Данные вариантов задачи 1 приведены в табл. 5 и на рис. 1 – 15, где
m
– масса газа; μ
–
молярная масса; i
– число степеней свободы;
![]() –
количество вещества в молях;Q1
– теплота, полученная газом от нагревателя;
Q2
– теплота, переданная газом охладителю;
А
– работа, совершаемая газом за один
цикл; ηТ
– термический КПД цикла; ηК
– КПД идеальной машины, работающей по
циклу Карно.
–
количество вещества в молях;Q1
– теплота, полученная газом от нагревателя;
Q2
– теплота, переданная газом охладителю;
А
– работа, совершаемая газом за один
цикл; ηТ
– термический КПД цикла; ηК
– КПД идеальной машины, работающей по
циклу Карно.
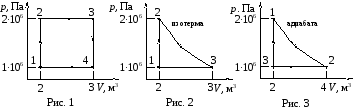
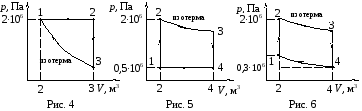



Таблица 5
