
Vischa_matematika_Dovidnik
.pdf
Вища математика |
|
Зміст |
|
І. Аналітична геометрія на площині. ................................................................ |
1 |
II. Диференціальне числення функцій однієї змінної. ..................................... |
2 |
III. Інтегральне числення. ................................................................................. |
3 |
ІV. Комплексні числа, визначники та системи рівнянь. ................................... |
7 |
V. Елементи векторної алгебри........................................................................ |
8 |
VI. Аналітична геометрія в просторі................................................................. |
8 |
VII. Диференціальне числення функції декількох змінних. ............................. |
9 |
VIII. Ряди.......................................................................................................... |
10 |
IX. Диференціальні рівняння. ......................................................................... |
11 |
Х. Криволінійні інтеграли. ............................................................................... |
12 |
XI. Подвійні та потрійні інтеграли. .................................................................. |
14 |
І. Аналітична геометрія на площині.
1. Паралельне перенесення системи координат:
х'=х-а, у'=у-в,
де О' (а; в) - новий початок, (х;у) - старі координати точки, [х';у'] - її нові координати.
2. Поворот системи координат (при нерухомому початку):
х = х'cos - у'sin ; y= x'sin + y'cоs ,
де (х,у) - старі координати точки, [х',у'] - її нові координати, - кут повороту.
3. |
Відстань між точками (х1,у1) і (х2,у2): |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
d= (х |
2 |
х )2 |
( у |
2 |
у )2 |
||||
|
|
|
|
|
1 |
|
1 |
|
||
4. |
Координати точки, що ділить відрізок з кінцями (х1,у1) і (х2,у2) в даному |
|||||||||
відношенні : |
|
|
|
|
|
|
|
|||
|
x= |
x1 x2 |
; |
y= |
y1 y2 |
. |
||||
|
|
1 |
|
|
|
|
1 |
|||
При =1, маємо координати середини відрізка:
|
|
х= |
x1 x2 |
; |
у= |
y1 y2 |
. |
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
5. Площа трикутника з вершинами (х1,у1), (х2,у2) і (х3,у3): |
||||||||||||||
S= |
1 |
(x |
|
x )( y |
|
y ) (x |
|
x )( y |
|
y ) . |
||||
|
2 |
3 |
3 |
2 |
||||||||||
|
2 |
|
1 |
1 |
|
|
1 |
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Рівняння прямої з кутовим коефіцієнтом:
у=кх+в,
де к=tg (кутовий коефіцієнт) - нахил прямої до осі Ох, в - довжина відрізка, що відтинає пряма на осі Оу.
7. tg = |
k k |
- тангенс кута між прямими з кутовими коефіцієнтами к і к/. |
|
|
|||
|
|
||
1 k k |
|
||
Умова паралельності прямих: к/=к.
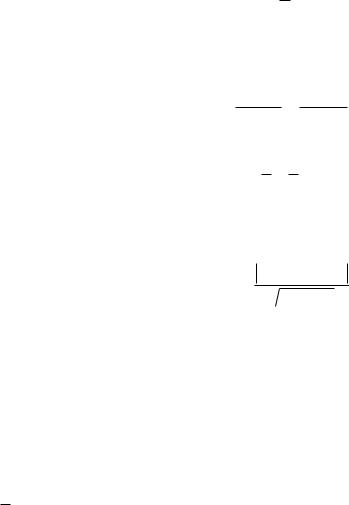
Умова перпендикулярності прямих: к/= 1k .
8. Рівняння прямої, що проходить через дану точку (х1,у1):
у-у1=к(х-х1)
9.Рівняння прямої, що проходить через дві точки (х1,у1) і (х2,у2):
xx1 y y1
x2 x1 y2 y1
10. Рівняння прямої, що відтинає відрізки а і в на осях координат:
ax by 1
11. Загальне рівняння прямої:
Ах+Ву+С=0, (А2+В2 0).
12. Відстань від точки (х1,у1) до прямої Ах+Ву+С=0:
= Ax1 By1 C
 A2 B 2
A2 B 2
13. Рівняння кола з центром (х0,у0) і радіусом R:
(х-х0)2+(у-у0)2=R2
14. Канонічне рівняння еліпса з півосями а і в:
x2 |
|
y 2 |
1 (1) |
|
a 2 |
b2 |
|||
|
|
Фокуси еліпса F(c;0) i F/(-c;0), де с2=а2-в2 15. Фокальні радіуси точки (х,у) еліпса (1):
r=a-Ex; r/=a+Ex,
де Е= ac 1 - ексцентриситет еліпса.
16. Канонічне рівняння гіперболи з півосями а і в:
x2 |
|
y 2 |
1 (2) |
|
a 2 |
b2 |
|||
|
|
нерівностями a x b, y1(x) y y2(x), z1(x, y) z z2(x, y)
де yi(x), zі(x, y), (і=1, 2) – неперервні функції, то потрійний інтеграл в прямокутних координатах від неперервної функції f(x, y z) можна обчислити за формулою:
|
|
b |
y2 ( x) z2 |
( x, y) |
|
|
f (x, y, z)dxdydz dx dy |
f (x, y, z)dz . |
|||
|
V |
a |
y1 ( x) z1 ( x, y) |
|
|
24. Параметричні рівняння еліпса з півосями а і в: |
|
|
|||
|
x=a cos t, |
y=b sin t. |
|
||
25. Параметричні рівняння циклоїди: |
|
|
|
|
|
|
x=a(t-sin t), |
|
y=a(1-cos t). |
|
|
II. Диференціальне числення функцій однієї змінної. |
|||||
1. Основні теореми про границі: |
|
|
|
|
|
|
а) lim[ f (x) g(x) h(x)] lim f (x) lim g(x) lim h(x). |
||||
|
x a |
|
x a |
x a |
x a |
|
б) lim[ f (x) * g(x)] lim f (x) * lim g(x) |
|
|||
|
x a |
|
x a |
x a |
|
Зокрема, lim[cf (x)] c lim f (x) |
|
|
|
|
|
x a |
x a |
|
|
|
|

|
|
в) lim[ |
f (x) |
] lim f (x) : lim g(x), (lim g(x) 0). |
||||||
|
|
g(x) |
||||||||
|
|
x a |
x a |
|
|
x a |
x a |
|||
2. |
Чудові границі: |
|
|
|
|
|
|
|
|
|
|
а) lim |
sin x |
1; |
б) lim(1 |
1 |
) x lim 1 1 e 2,7182. |
||||
|
|
|
|
|||||||
|
x 0 |
x |
|
x |
x |
0 |
||||
3. |
Зв'язок між десятковими та натуральними логарифмами: |
|||||||||
|
|
lg x=М ln x, де М=lg e=0,43429… |
||||||||
4. |
Приріст функції у=f(x), що відповідає приросту x аргументу х: |
|||||||||
|
|
|
|
|
y f (x x) f (x). |
|||||
5. |
Умова неперервності функції у=f(x): |
|
|
|
|
|||||
|
|
|
|
|
lim y 0 |
|
||||
|
|
|
|
|
x 0 |
|
|
|||
Основна властивість неперервної функції: |
|
|
||||||||
|
|
|
|
|
lim f (x) f (lim x). |
|||||
|
|
|
|
|
x x1 |
|
|
x x1 |
||
6. |
Похідна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
dy |
|
lim |
y . |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
dx |
|
|
x 0 |
x |
Геометрично y /=f /(x) - кутовий коефіцієнт дотичної до
III. Інтегральне числення.
1.Якщо dy=f(x)dx, то y= f (x)dx (незвичайний інтеграл).
2.Основні властивості незвичайного інтеграла:
а) d f (x)dx f (x)dx |
[ f (x)dx] f (x); |
б) dF(x) F(x) C; |
в) Af (x)dx A f (x)dx; (А0) |
г) [ f (x) g(x) h(x)]dx f (x)dx g(x)dx h(x)dx
Таблиця найпростіших невизначених інтегралів.
1) xm dx |
xm 1 |
|
C |
(m -1). |
|
m 1 |
|||||
|
|
|
|||
2)dxx ln x C , (при х<0 i при x>0).
3)e x dx e x C ;
4) |
a x dx |
a x |
C, |
(a>0, a 1). |
|
ln a |
|||||
|
|
|
|
||
5) |
cos xdx sin x C . |
|
|||
де h=(b-a)/n, x0=a, xn=b, y=f(x), yi=f(x0+ih), (i=0,1,2,…,n).
|
|
b |
h |
|
|
a b |
|
|
|
ydx |
|
||||
11. |
Формула Сімпсона: |
|
y(a) 4 y( |
|
) y(b) , |
||
|
|
||||||
|
|
a |
3 |
|
|
2 |
|
де h=(b-a)/2. |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
12. |
Невласний інтеграл: |
f (x)dx lim |
f (x)dx. |
|
|||
|
|
|
|
b |
|
|
|
a |
a |

13. Площа криволінійної трапеції обмеженої неперервною лінією у=f(x) (f(x) 0),
b
віссю Ох і двома вертикалями х=а, х=b (a<b): S f (x)dx .
a
14. Площа сектора обмеженого неперервною лінією =f( ) ( i - полярні
координати) і двома промінями = , = ( < ): S 1 2 d .
2
15. Довжина дуги гладкої кривої y=f(x) в прямокутних координатах х і у від точки х=а до точки х=b (a<b):
b
l 
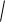 1 y 2 dx .
1 y 2 dx .
a
16. Довжина дуги гладкої кривої =f( ) в полярних координатах і від точки
= до точки = ( < ):
l 
 2 2 d ,
2 2 d ,
17. Довжина дуги гладкої кривої х= (t) y= (t), задано параметрично (t0<T):
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
x 2 y 2 dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18.Об’єм тіла з відомим поперечним перерізом S(x): |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
||||||
9. Ряд Маклорена. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
f (0) f (0)x |
|
|
f (0) |
|
x2 ... |
f (n) (0) |
|
xn |
... |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
n! |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
10. Розклад в степеневі ряди функцій: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
а) |
1 |
1 x x |
2 ... xn |
... , при x < 1; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
1 x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) ln(1+x) = x |
x2 |
|
|
|
x3 |
|
|
|
x4 |
|
|
... ( 1)n 1 |
xn |
|
|
... , при –1<x 1; |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
n |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
в) arctgx x |
x3 |
|
|
|
|
x5 |
|
|
|
|
x7 |
|
|
... ( 1)n 1 |
x2n 1 |
|
|
... , при x 1; |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
5 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
г) |
e x 1 x |
x2 |
|
|
x3 |
|
... |
xn |
|
..., при x < +; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2! |
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x3 |
|
|
|
|
|
x5 |
|
|
|
x7 |
|
... ( 1)n 1 |
|
|
x2n 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
д) sin x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... , |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
3! |
|
|
|
|
|
5! |
|
|
|
|
|
|
7! |
|
|
|
|
|
|
|
|
|
|
|
(2n 1)! |
|
|
|
|
|
|
|
||||||||||||||||||||||
при x < +; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
е) |
cos x 1 |
x2 |
|
x4 |
|
x6 |
|
... ( 1)n |
x2n |
|
... |
, при x < +; |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2! |
|
|
|
|
|
4! |
|
|
|
|
|
|
6! |
|
|
|
|
|
|
|
|
|
|
(2n)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ж) |
(1 x)m 1 mx |
m(m 1) |
x2 |
... |
m(m 1)...[m (n 1)] |
xn ... , |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 ... n |
|
|
|
|
|
|
||||||||||||||
при x < 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
11. Ряд Тейлора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
f (x) f (a) f (a)(x a) |
|
f (a) |
(x a)2 ... |
f (n) (a) |
(x a)n ... |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2! |
|
|
n! |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
12. Ряди в комплексній області: (U n iVn ) U n i Vn . |
||
n 1 |
n 1 |
n 1 |
13. Абсолютна збіжність рядів з коиплексними членами. Якщо ряд
|
|
|
|
|
||
|
|
|||||
|
|
U n iVn |
|
U n2 Vn2 збігається, то ряд |
||
|
|
|||||
n 1 |
|
n 1 |
||||
19
(U n iVn ) також збігається (абсолютно).
n 1
14.Формули Ейлера: eix cos x i sin x , e ix cos x i sin x .
15.Тригонометричний ряд Фур є кусково-гладкої функції f(x) періоду 2l має вигляд:
|
|
a0 |
|
|
|
|
n x |
|
|
n x |
|
|||||
f (x) |
|
(an |
cos |
bn sin |
) , (1) |
|||||||||||
2 |
|
|
l |
|
||||||||||||
|
|
|
n 1 |
|
|
|
|
|
|
l |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де an |
|
|
1 l |
f (x) cos |
n x |
dx |
, |
(n=0, 1, 2,…); |
||||||||
|
|
|
|
|
|
|||||||||||
|
l |
|
|
|||||||||||||
|
|
|
|
|
l |
|
|
|
|
|||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|||
b |
|
1 l |
f (x) sin |
n x |
dx , |
(n=1, 2,…). |
||||||||||
|
|
|
|
|
||||||||||||
|
l |
|
||||||||||||||
n |
|
|
|
|
l |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l
(коефіцієнти Фур є функції f(x)). Для функції f(x) періоду 2 маємо
|
a0 |
|
|
f (x) |
(an cos nx bn sin nx) |
||
|
|||
2 |
n 1 |
||
|
|
||
де
В точках розриву функцій f(x)
,
|
1 |
|
|
|
|
|
|
cos nx |
|
||
|
|
|
f (x) |
dx , (n=0, 1, 2,…). |
|
|
|||||
|
|
sin nx |
|
сума ряду (1) дорівнює
|
|
|
S(x) |
1 |
|
f (x 0) f (x 0) |
||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. Якщо 2l – періодична функція f(x) парна, то |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
n x |
|
||||||
|
|
|
|
f (x) |
|
an cos |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
n 1 |
|
|
|
|
l |
||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|||
|
де |
an |
2 |
l |
f (x) cos |
n x |
dx , |
(n=0,1, 2,…). |
||||||||||||||
|
|
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо 2l – періодична функція f(x) непарна, то |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n x |
|
|
|
|||||||
|
|
|
|
|
f (x) bn |
sin |
, |
|
||||||||||||||
|
|
|
|
|
l |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
m 1 |
|
|
|
||||
|
|
f (x)dx |
|
|
|
lim |
|
|
f ( |
xi |
) xi , |
|||||||||||
де x xi , xi 1 і xi |
|
a |
|
|
|
|
max |
|
xi |
|
0 i 0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
xi 1 xi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. Основні властивості визначеного інтегралу (розглядувані функції неперервні):
b |
b |
b |
|
а) f (x)dx f (t)dt ; |
б) f (x)dx 0; |
||
a |
a |
a |
|
b |
a |
b |
b |
в) f (x)dx f (x)dx; |
г) |
Af (x)dx A f (x)dx; |
|
a |
b |
a |
a |
c |
b |
b |
|
д) f (x)dx f (x)dx |
f (x)dx; |
|
|
a |
c |
a |

|
b |
|
|
|
|
|
|
|
|
|
|
|
b |
b |
b |
|
|
|
|
|||
е) f (x) g(x) h(x) dx f (x)dx |
g(x)dx h(x)dx; |
|||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
a |
a |
|
|
|
|
|||
|
|
d |
x |
|
|
|
|
|
|
d |
b |
|
|
|
|
|
|
|
|
|||
ж) |
|
|
f (t)dt f (x), |
f (t)dt f (x) |
|
|
|
|
|
|||||||||||||
|
dx |
dx |
|
|
|
|
|
|||||||||||||||
|
|
a |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. Теорема про середнє: якщо f(x) - неперервна на [a,b], то |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx (b a) f (c) , |
де а<c<b. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
8. Формула інтегрування частинами у визначеному інтегралі: |
||||||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
u(x)v (x)dx u(x)v(x) |
ba v(x)u (x)dx |
|
|
|
|
|
||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
9. Формула заміни змінної у визначеному інтегралі: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
де а= ( ), b= ( ). |
||||
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx f ( (t)) (t)dt, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
1 |
|
|
|
|
1 |
|
|
10. Формула трапецій: |
ydx h( |
y0 y1 |
... yn 1 |
|
yn ) , |
|||||||||||||||||
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=r(cos +isin ), де r= z ; =Arg z |
||||||||
5. Теореми про модуль та аргумент: |
|
|
|
|
|
|||||||||||||||||
а) z1+z2 z1 + z2 ; |
б) z1z2 z1 z2 , |
|
|
|
|
|||||||||||||||||
Arg z1z2=Arg z1+Arg z2; |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
z |
|
|
|
z1 |
|
|
z |
|
=Arg z1-Arg z2; (z2 0); |
|
|
|
|
|||||||
в) |
1 |
|
|
|
; |
Arg |
|
1 |
|
|
|
|
||||||||||
z2 |
|
|
z2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|||||||
г) zn = z n; Arg zn=n Arg z |
(n - ціле). |
|
|
|
|
|||||||||||||||||
6. Корінь з комплексного числа: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
arg z 2k |
|
|
|
|
|
|
|
|
|
|||
n |
z n |
|||||||||
|
|
|||||||||
|
|
z |
|
|
cos |
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||
i sin |
arg z 2k |
, (k=0,1,2,…,n-1) |
|
|
|
||
|
|||
|
n |
|
|
7. Показникова формула комплексного числа:
z= r ei , де z = z , = Arg z.
8.Визначник другого порядку:
9. Розв’язок системи a1 x b1 y C1
a2 x b2 y C2
a1 |
b1 |
a b a b . |
|||
a2 |
b2 |
1 |
2 |
2 |
1 |
|
|
|
|
||
знаходяться за формулами: х= х/ ; у= у/
(правило Крамера), де
|
a1 |
b1 |
0; x |
c1 |
b1 |
; y |
a1 |
c1 |
. |
||||
|
a |
2 |
b |
|
c |
2 |
b |
|
a |
2 |
c |
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
||||
10. Розв’язок однорідної системи: a1 x b1 y c1 z 0 визначається за формулами:
a2 x b2 y c2 z 0
х= 1t, y=- 2t, z= 3t; (- <t< ),
де |
1 |
|
b1 |
c1 |
, 2 |
|
a1 |
c1 |
, 3 |
|
a1 |
b1 |
- |
|
|
|
b2 |
c2 |
|
|
a2 |
c2 |
|
|
a2 |
b2 |
|

|
|
|
|
a1 |
b1 |
||
|
|
мінори матриці |
|
|
|||
|
|
|
|
|
|
b2 |
|
|
|
|
|
a2 |
|||
z |
lim |
f (x x, y) f (x, y) |
; |
z |
lim |
||
x |
x |
y |
|||||
x 0 |
|
|
y 0 |
||||
1. c2
f (x, y y) f (x, y)
y
3. Повний диференціал функції z = f(x, y) від незалежних змінних х, у:
dz |
z |
dx |
|
z |
dy, |
де dx= x, |
dy= y. |
||||||||
|
|
|
|||||||||||||
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|||
Якщо U = f(x, y, z), то du |
u |
dx |
u |
dy |
u |
dz . |
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
x |
y |
|
z |
|
|
|
||||||||
4. Малий приріст диференційованої функції: |
|
|
|
||||||||||||
|
|
|
|
|
z |
z |
x |
z |
y, |
|
|||||
|
|
|
|
|
x |
y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Похідна функції U = f(x, y) по напряму l, заданому одиничним вектором {cos , cos } дорівнює:
u |
|
u cos |
u cos . |
l |
|
x |
y |
Аналогічно, якщо U = f(x, y, z) і {cos , cos , cos } – одиничний вектор напряму l, то
u |
|
u cos |
u cos |
u cos |
l |
|
x |
y |
z |
6. Точки можливого екстремуму диференціальної функції U = f(x, y, z) визначаються з рівнянь:
f х(x, y, z)=0; |
f y(x, y, z)=0; |
f z(x, y, z)=0 |
|||||
7. Градієнтом скалярного поля U = f(x, y, z) є вектор |
|||||||
|
|
u |
, |
u |
, |
u |
|
gradU |
|
|
|
|
|||
|
|
x |
|
y |
|
z |
|
|
|
|
|
u |
|
2 |
|
u 2 |
|
u |
|
2 |
|
Звідси |
gradU |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
. |
||||||
|
|
|
x |
|
|
|
|
z |
|
||||
|
|
|
|
|
y |
|
|||||||
8. Якщо P(x, y)dx + Q(x, y)dy є повним диференціалом в області G, то
P |
|
Q |
((x, y) є G). |
y |
|
x |
|
(ознака повного диференціалу.).
ІV. Комплексні числа, визначники та системи рівнянь.
1. Комплексне число z=x+iy, де х=Re z, y=Im z - дійсні числа, і2=-1. Модуль комплексного числа:
z 
 x2 y 2 0.
x2 y 2 0.
Рівність комплексних чисел:
z1=z2 Re z1=Re z2, Im z1=Im z2
2. Спряжене число для комплексного числа z=x+iy: z x iy
3. Арифметичні дії над комплексними числами z1=x1+iy1, z2=x2+iy2:
a) z1 z2 x1 x2 i y1 y2 ;
б) z1 z2 x1 x2 y1 y2 i x1 y2 x2 y1 ;

в) |
|
z1 |
|
|
z1 z |
2 |
|
x1 x2 y1 y2 i x2 y1 x1 y2 |
; |
(z2 0) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
z2 |
|
|
z |
2 |
2 |
|
x22 y |
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Зокрема Re z =1/2 (z+ z ), Im z= (z- z )/2і, z 2=z z . |
||||||||||||||||||||||||||||||||||||
V. Елементи векторної алгебри. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1. |
Сумою векторів a , b , |
|
|
|
є вектор S a b c . |
|||||||||||||||||||||||||||||||
c |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2. |
Різницею векторів a і b |
є вектор d a b a ( b ) , де |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
- b |
|
- вектор, протилежний вектору b . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3. |
|
|
|
|
* a , де a |
|
і |
|||||||||||||||||||||||||||||
Добутком вектора a на скаляр k є вектор b ka такий що b |
k |
a |
||||||||||||||||||||||||||||||||||
b b , причому напрям вектора b співпадає з напрямком вектора a , якщо k > 0, і
протилежний до нього, якщо k < 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4. |
Вектор a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
і b колінеарні, якщо b ka (k - скаляр). |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вектори a , |
b , |
|
компланарні, якщо c ka lb ,(k,l-скаляри) |
|||||||||||||||||||||||||||||||||
c |
||||||||||||||||||||||||||||||||||||
5. |
Скалярним добутком векторів a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
і b є число |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
a |
b |
cos , |
де |
=<( a , b ). |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|||||||||||||||
Вектори a і b ортогональні, якщо a * b |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Якщо a ax , ay , az і |
|
bx ,by ,bz , то a * |
|
|
axbx |
ay by az bz . |
||||||||||||||||||||||||||||||
b |
b |
|||||||||||||||||||||||||||||||||||
6. |
Векторним добутком векторів a |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
і b є вектор c a * b , |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c a |
|
sin , ( = <(a,b)), |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
де c a, c b , |
|
b |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
причому а, b, с - права трійк. |
|||||||||||||||||||||||||||
Якщо a ax , ay , az і b bx ,by ,bz , то a * |
|
|
|
|
|
|
|
i |
j |
k |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
ax |
|
|
, де |
|||||||||||||||||||||||||||||||
b |
a y |
az |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bx |
by |
bz |
|
|||||||
i, j, k - одиничні вектори (орти), напрямлені згідно з відповідними осями координатами.
7. Мішаний добуток ab c a *b * c являє собою об’єм (зі знаком) паралелепіпеда, побудованого на векторах а, b, с.
Якщо a ax , ay , az , |
b bx ,by ,bz , |
c cx , cy , cz , то |
||||||
|
|
|
|
|
ax |
a y |
az |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
ab c |
bx |
by |
bz |
. |
||
|
|
|
|
|
cx |
cy |
cz |
|
|
|
|
|
|
|
|
|
|
VI. Аналітична геометрія в просторі.
1. Декартові прямокутні координати точки М(х, у, z) простору Охуz є:
x=rx , y=ry , z=rz , де r= OM - радіус-вектор точки М. 2. Довжина та напрям вектора а={ax,ay,az} визначаються формулами:
a a 
 ax2 ay2 az2 ;
ax2 ay2 az2 ;
cos =ax/a; cos =ay/a; cos =az/a, (cos2 +cos2 +cos2 =1),
де cos , cos , cos - напрямні косинуси вектора а. 3. Відстань між двома точками M1(x1,y1,z1) i M2(x2,y2,z2):

d M1M 2  (x2 x1 )2 ( y2 y1 )2 (z2 z1 )2 .
(x2 x1 )2 ( y2 y1 )2 (z2 z1 )2 .
4.Рівняння площини з нормальним вектором N={A,B,C} 0, що проходить через точку M0(x0,y0,z0) є N (r-r0)=0,…(1)
де r - радіус-вектор текучої точки площини M(x,y,z) і r0 - радіус-вектор точки М0. В координатах рівняння (1) має вид:
А(х-х0)+В(у-у0)+С(z-z0)=0 або Ax+By+Cz+D=0 (2)
де D= -Ax0-By0-Cz0 (згальне рівняння площини).
5.Відстань від точки M1(x1,y1,z1) до площини (2) дорівнює:
d Ax1 By1 Cz1 D
 A2 B2 C 2
A2 B2 C 2
6. Векторне рівняння прямої лінії в просторі: r=r0+st (3)
15
де r{x,y,z} - текучий радіус-вектор прямої; r0{x0,y0,z0} - радіус-вектор фіксованої точки прямої, s{m,n,p} 0 - напрямний вектор прямої і t - параметр (- <t<+ ).
Вкоординатній формі рівняння прямої (3) має вигляд:
xx0 y y0 z z0 . m n p
7.Пряма лінія як перетин площин визначається рівняннями: Ax By Cz D 0
A x B y C z D 0
(4)
Напрямним вектором прямої (4) є S=N N , де N={A,B,C}, N ={A ,B ,C }. 8. Рівняння сфери радіуса R з центром (x0,y0,z0):
(x x0 )2 ( y y0 )2 (z z0 )2 R2 .
9. Рівняння трьохосьового еліпса з півосями a,b,c:
x2 |
|
y 2 |
|
z 2 |
1. |
|
a 2 |
b2 |
c2 |
||||
|
|
|
10. Рівняння параболоїда обертання навколо осі Оz: x2+y2=2pz.
VII. Диференціальне числення функції декількох змінних.
1. Умова некперервності функції z=f(x,y): |
|
|
lim z lim f (x x, y y) f (x, y) 0 |
, |
|
x0 |
x0 |
|
y 0 |
y 0 |
|
або lim f (x1, y1) f (x, y)
x1 x y1 y
Аналогічно визначається неперервність функції f(x, y, z). 2. Частинні похідні функції z = f(x, y) по змінних х, у:
16
11. Визначник третього порядку:

|
a1 |
b1 |
c1 |
|
|
a2 |
b2 |
c2 |
a1 A1 b1 B1 c1C1 , |
|
a3 |
b3 |
c3 |
|
де |
A |
b2 |
c2 |
; B |
|
a2 |
|
c2 |
;C |
|
a2 |
b2 |
- алгебраїчні |
|||
|
1 |
|
b3 |
c3 |
1 |
|
|
a3 |
|
c3 |
1 |
|
a3 |
b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
доповнення відповідних елементів визначника. |
|
|
||||||||||||||
|
a1 x b1 y c1 z d1 |
|
|
|
|
|
|
|||||||||
12. Розв’язок системи a2 x b2 y c2 z d2 |
визначається за формулою Крамера |
|||||||||||||||
|
a |
x b y c |
3 |
z d |
3 |
|
|
|
|
|
|
|||||
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|||
х= х/ ; у= у/ ; z= z/ ,
|
a1 |
b1 |
c1 |
|
|
|
де |
a2 |
b2 |
c2 |
0; |
|
|
|
a3 |
b3 |
c3 |
|
|
|
|
|
|
|
|
a1 |
d1 |
|
|
|
|
|
||
|
|
|
|
y |
a2 |
d2 |
|
|
|
|
|
a3 |
d3 |
13. Розв’язок однорідної системи
a1
a2 a3
|
|
|
|
d1 |
b1 |
|
|
c1 |
|
|
|
|
|
|
|
|
|
x |
d2 |
b2 |
|
|
c2 |
, |
|
|
|
|
|
||||||
|
|
|
|
d3 |
b3 |
|
|
c3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 |
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
b1 |
d1 |
|
|
c2 |
, |
|
|
|
|
|
|
z |
a2 |
|
b2 |
d2 |
. |
||||
c3 |
|
|
|
|
|
|
|
|
|
|
|
a3 |
|
b3 |
d3 |
|
|
a x b y c z 0 |
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
a2 x b2 y c2 z 0 , якщо |
|
|
|||||||||||||||
a |
3 |
x b y c |
3 |
z 0 |
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
b1 |
|
c1 |
0, |
|
|
|
a1 |
b1 |
|
0, |
|
|
|||||
|
|
|
|
|
|
||||||||||||
b c |
2 |
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
||
b3 |
|
c3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a x b y c z 0
знаходяться з підсистеми: 1 1 1 .
a2 x b2 y c2 z 0
VIII. Ряди.
1.Основне означення: U n
n 1
N
lim U n .
N n 1
2. |
Необхідна ознака збіжності ряду: |
|
|
||||
|
|
|
|
|
|
|
|
|
якщо ряд U n |
збігається, то lim U n 0 . |
|||||
|
n 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
a |
|
|
3. |
Геометрична прогресія: aq n 1 |
|
|
, якщо q < 1. |
|||
1 |
q |
||||||
|
|
n 1 |
|
||||
|
|
|
|
|
|
||
4. |
Гармонічний ряд 1 + 1/2 + 1/3 + … (розбігається). |
||||||
|
|
|
|
|
|
|
|
5. |
Ознака Даламбера. Нехай для ряду U n (Un>0) існує |
||||||
n 1
lim U n 1 l U n
Тоді: а) Якщо l < 1, то ряд збігається;
б) Якщо l > 1, то ряд розбігається, Un непрямує до 0.
