Несинусоїдний струм

Несинусоїдні струми і напруги в електричних колах виникають при дії джерел несинусоїдної ЕРС (струму) або за наявності в колі нелінійних елементів.

В лінійних електричних колах з періодичними несинусоїдними джерелами живлення струму і напруги теж є періодичними функціями часу. Всяку періодичну несинусоїдну ЕРС, напругу чи струм можна розкласти в тригонометричний (гармонічний) ряд Фур’є:

(8.1)

де – постійна складова,

–основна або перша гармоніка,

–вища гармоніка порядку (-та гармоніка).

Розклавши синус суми для кожної гармонічної складової

,

можна записати ряд Фур’є в іншій формі:

(8.2)

Тут ,.

Якщо функція задана аналітично, то коефіцієнти,,визначають за формулами:

,

, (8.3)

.

Знаючи і,легко визначити амплітуду і початкову фазу-тої гармоніки:

, . (8.4)

За наявності в періодичній функції певного виду симетрії її розкладання в ряд Фур’є спрощується. Зокрема, якщо функція є симетричною відносно осі абсцис (рисунок 8.1), тобто задовольняє умові , то ряд Фур’є не містить постійної складової і парних гармонік, тобто:

Рисунок 8.1 – Крива, симетрична відносно осі абсцис

Якщо функція симетрична відносно осі ординат (рисунок 8.2), тобто задовольняє умові , то ряд Фур’є не містить синусних складових:

Якщо функція симетрична відносно початку координат (рисунок 8.3), тобто задовольняє умові , то в розкладі відсутні постійна і косинусні складові:

Якщо крива струму чи напруги задана графічно, то можна використати графоаналітичний метод розкладання в ряд Фур’є, оснований на заміні визначеного інтеграла сумою скінченого числа складових. З цією метою період функції , що дорівнює, розділяють нарівних інтервалів(рисунок 8.4) і визначають коефіцієнти,,за формулами:

,

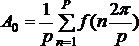, (8.5)

.

Тут – порядковий номер інтервалу, а– значення функції в кінці кожного інтервалу.

Діюче значення несинусоїдного струму чи напруги можна визначити через постійну складову і діючі значення гармонік:

(8.6)

В колі з джерелом періодичної несинусоїдної напруги криві струмів будуть відтворювати форму кривої напруги лише у випадку, якщо коло складається з резистивних елементів, опір яких одинаковий для всіх частот. В колі з індуктивними і ємнісними елементами крива струму буде відрізнятись за формою від кривої напруги джерела, оскільки опір такого кола залежить від частоти. З підвищенням порядку гармоніки індуктивний опірзростає, а ємнісний опірзменшується. Тому в колі з послідовним з’єднанням,– елементів вищі гармоніки струму виражені слабше, ніж в напрузі джерела. В колі з послідовним з’єднанням,– елементів, навпаки, вищі гармоніки струму виражені сильніше ніж в напрузі джерела.

В електроенергетичних мережах криві напруг і струмів звично симетричні відносно осі абсцис. Для оцінки ступеня їх несинусоїдності користуються відповідними коефіцієнтами, зокрема:

· коефіцієнтом амплітуди ; для синусоїди;

· коефіцієнтом спотворення ; для синусоїди;

· коефіцієнтом форми ; для синусоїди,

а також відношенням амплітуд ,

де ,,– максимальне, діюче і середнє за модулем значення несинусоїдної функції відповідно,– діюче значення першої гармоніки, аі– амплітуди відповідно першої і-тої гармоніки.