5. Вычисление статических моментов и координат центра тяжести плоской фигуры

Пусть дана материальная плоская фигура (пластинка), ограниченной кривой у=f(х)≥0 и прямыми у=0, х=а, х =b) (рис 7).

рис 7

Будем считать, что поверхностная плотность пластинки постоянна (=const). Тогда масса всей пластинки равнат.е.

Выделим элементарный участок пластинки в виде бесконечно узкой вертикальной полосы и будем приближенно считать его прямоугольником.

Тогда масса его равна . Центр тяжестипрямоугольника лежит на пересечении диагоналей прямоугольника. Эта точкаотстоит от оси Ох на, а от оси Оу на x (приближенно; точнее на расстоянии). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения

Следовательно,

По аналогии с плоской кривой получаем, обозначив координаты центра тяжести плоской фигуры (пластинки) через С(), что.

Отсюда

Или

4. Примеры.

Задание 1. Найти длину окружности радиуса R

Решение: Найдем часть ее длины от точки (0;R). Так как

Задание 2. Вычислить объем V кругового конуса с радиусом основания r и высотой h

Решение: проведем через ось конуса секущую плоскость и выберем эту ось за ось х,считая начальной точкой вершину конуса; ось у проведем перпендикулярно к оси конуса. Уравнение образующей конуса будет

и по формуле

получим:

Задание 3: Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела v(t)=10t+2 (м/с).

Решение: Если v(t)=10t+2 (м/с), то путь, пройденный телом от начала движения (t =0) до конца 4-й секунды, равен

Задание 4: Найти объем тела, образованного вращением фигуры, ограниченной линиями ,,вокруг оси

Решение:

Аналогично можно доказать, что объём тела, полученного вращением вокруг оси Оу можно вычислить по формуле

Задание 5. Вычислить массу стержня на отрезке от 0 до 2, если его плотность задаётся функцией (слайд 19)

Решение:

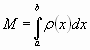
Задание 6. Вычислить площадь фигуры, ограниченной линиями .

Решение.

Находим точки пересечения заданных линий. Для этого решаем систему уравнений:

Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:

или    .

Находим: x₁ = -2, x₂ = 4.

Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).

Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:

По формуле Ньютона-Лейбница находим: