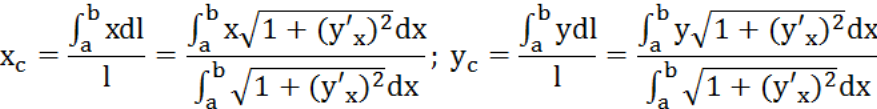2. Вычисление площади плоской фигуры

Пусть функция непрерывна на сегментеЕслина [a,b], то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, равна интегралу

Если же нато —наПоэтому площадь S соответствующей криволинейной трапеции выразится формулой

Если, наконец, кривая пересекает ось Ох, то сегментнадо разбить на части, в пределах которыхне меняет знака, и к каждой такой части применить ту из формул, которая ей соответствует.

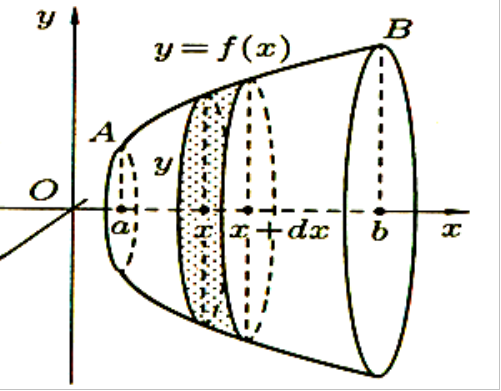
3. Вычисление площади поверхности вращения

Пусть кривая АВ является графиком функции , где, а функцияи ее производнаянепрерывны на этом отрезке.

Найдем площадь поверхности, образованной вращением кривой АВ вокруг оси.

Применим схему II (метод дифференциала).

1. Через произвольную точку проведем плоскость, перпендикулярную оси. Плоскость пересекает поверхность вращения по окружности с радиусом(рис. 5). Величинаповерхности части фигуры вращения, лежащей левее плоскости, является функцией от, т.е.

и

2. Дадим аргументу приращение. Через точкутакже проведем плоскость, перпендикулярную оси. Функцияполучит приращение. Найдем дифференциал площади, заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна, а радиусы оснований равныи. Площадь его боковой поверхности равна

Отбрасывая произведение как бесконечно малую высшего порядка, чемполучаем, или, так как

, то

3. Интегрируя полученное равенство в пределах получаем

.

Если кривая AB задана параметрическими уравнениями то формула для площади поверхности вращения принимает вид

3. Физические приложения определенного интеграла

1. Работа переменной силы

Пусть материальная точка М перемещается вдоль оси под действием переменной силынаправленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положенияв положениенаходится по формуле

2. Путь пройденный телом

Путь S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t=a до t=b, вычисляется по формуле

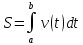
3. Масса неоднородного стержня

Масса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от плотности p(х):

4. Вычисление статических моментов и координат центра тяжести плоской кривой

Пусть на плоскости Оху задана система материальных точек соответственное массами

Статическим моментом S_Х системы материальных точек относительно оси Ох называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси Ох):

Аналогично определяется статистический момент этой системы относительно оси Oy:

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.

Пусть у =f(х) (a ≤ х ≤ b) — это уравнение материальной кривой АВ. Будем считать ее однородной с постоянной линейной плотностью (=const).

Для произвольного на кривой АВ найдется точка с координатами (х; у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого участка равна. Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента(“элементарный момент”) будет находиться по формуле:

Отсюда следует, что статический момент кривой АВ относительно оси Ох равен

Аналогично находим :

Статические моменты S_Х и S_У кривой позволяют легко установить положение ее центра тяжести (центра масс).

Центром тяжести материальной плоской кривой х вназывается точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу т заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой у = f(х) относительно той же оси. Обозначим через С(х_с;у_с) центр тяжести кривой АВ.

Из определения центра тяжести следуют равенства иилии. Отсюда,

или