Национальный исследовательский ядерный университет МИФИ.

Саровский физико-технический институт филиал НИЯУ МИФИ.

Кафедра высшей математики.

Реферат по математическому анализу на тему: “Геометрические и физические приложения определенного интеграла”.

Выполнил: студент группы ИТ-13Д

Теплякова Я.А

Проверил: К.п.н

доцент кафедры ВМ

Прокофьева Н.В

Саров-2013 г.

Содержание:

§1. Введение……………………………………………………………..Стр.3-5

§2. Геометрические приложения определенного интеграла…...стр.5-10

§3. Физический смысл определенного интеграла………..……..стр.10-14

§4. Примеры………14-

§5. Заключение.

§1. Введение.

Определенный интеграл – одно из основных понятий математического анализа – является мощным средством исследования в математике, физике, механике и других дисциплинах.

1. Определенный интеграл как предел интегральной суммы

Пусть функция определена на отрезке,. Выполним следующие действия.

1. С помощью точек разобьем отрезокначастичных отрезков

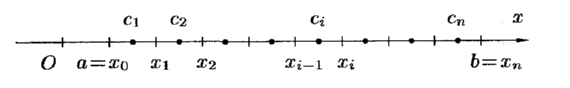
2. В каждом частичном отрезке выберем произвольную точкуи вычислим значение функции в ней, т.е. величину

3. Умножим найденное значение функции на длинусоответствующего частичного отрезка:

4. Составим сумму всех таких произведений:

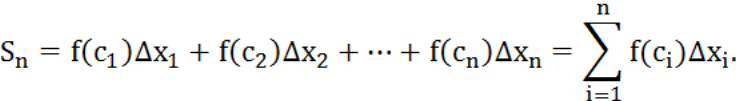
Сумма называется интегральной суммой функциина отрезке. Обозначим черездлину наибольшего частичного отрезка:

5. Найдем предел интегральной суммы, когда так, чтоЕсли при этом интегральная суммаимеет предел, который не зависит ни от способа разбиения отрезкана частичные отрезки, ни от выбора точек в них, то числоназывается определенным интегралом от функциина отрезкеи обозначается

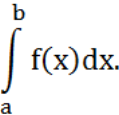
Таким образом,

Числа иназываются соответственно нижним и верхним пределами интегрирования,- подынтегральной функцией,- подынтегральным выражением,- переменной интегрирования, отрезок- областью (отрезком) интегрирования.

Функция , для которой на отрезкесуществует определенный интеграл, называется интегрируемой на этом отрезке.

Теорема: если функция непрерывна на отрезкеикакая-либо ее первообразная на, то имеет место формула

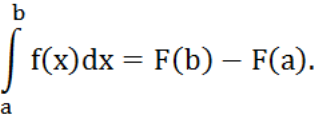
Формула Ньютона-Лейбница дает удобный способ вычисления определенного интеграла. Чтобы вычислить определенный интеграл от непрерывной функции на отрезке, надо найти ее первообразную функциюи взять ее разностьзначений этой первообразной на концах отрезка

§2. Геометрические приложения определенного интеграла.

1. Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений.

Пусть требуется найти объем тела, причем известны площадисечений этого тела плоскостями, перпендикулярными некоторой оси, например оси

Применим схему II (метод дифференциала).

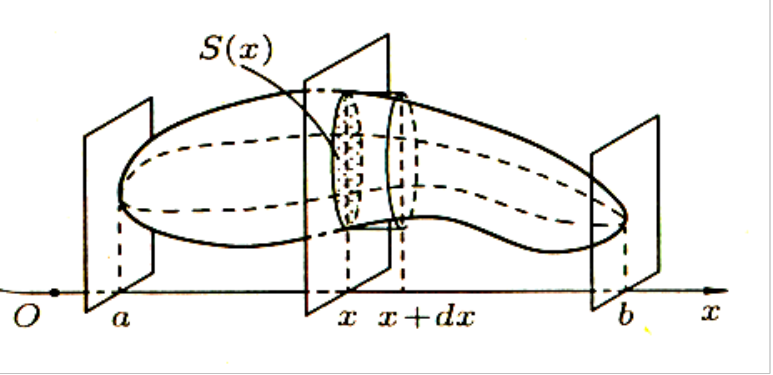
1. Через произвольную точку проведем плоскость, перпендикулярную оси(рис. 3). Обозначим черезплощадь сечения тела этой плоскостью;считаем известной и непрерывно изменяющейся при изменении. Черезобозначим объем части тела, лежащее левее плоскости. Будем считать, что на отрезкевеличинаесть функция от x, т. е.

2. Находим дифференциал функцииОн представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими осьв точках, который приближенно может быть принят за цилиндр с основаниеми высотой. Поэтому дифференциал объема.

3. Находим искомую величину путем интегрированияв пределах от

.

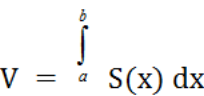Полученная формула называется формулой объема тела по площади параллельных сечений.

Объем тела вращения.

Пусть вокруг оси вращается криволинейная трапеция, ограниченная непрерывной линией, отрезкоми прямымии(рис. 4). Полученная от вращения фигура называется телом вращения.

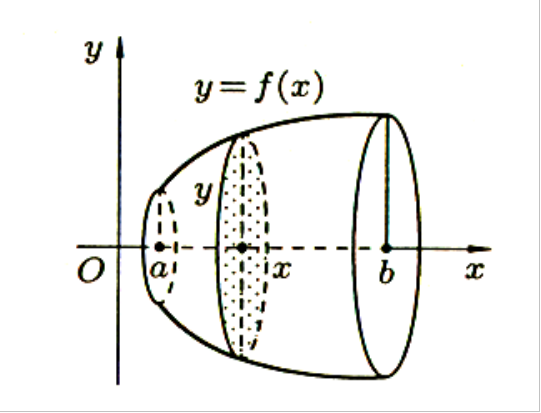
Сечение этого тела плоскостью, перпендикулярной оси , проведенной через произвольную точкуоси, есть круг с радиусом. Следовательно,

Применяя формулу (4) объема тела по площади параллельных сечений, получаемрис 4

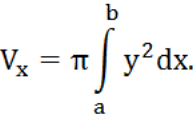
Если криволинейная трапеция ограничена графиком непрерывной функции и прямыми, то объем тела, образованного вращением этой трапеции вокруг оси, по аналогии с формулой (5), равен