Диапазон значений знаковых чисел

Рассмотрим однобайтовое представление. Возможные дополнительные коды знаковых чисел:

0111 1111

. . .

0000 0001

0000 0000

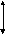1111 1111

1111 1110 Отрицательные числа

. . .

1000 0000

Рассмотрим десятичные значения этих чисел:

0111 1111 = 2⁷ – 1 = 128 - 1 = 127

0000 0001 = 1

0000 0000 = 0

1111 1111 -> -(000 0000 + 1) = -1

1111 1110 -> -(000 0001 + 1) = -2

1000 0000 -> -(111 1111 + 1) = -(1000 0000) = -2⁷ = -128

Таким образом диапазон значений знаковых однобайтовых чисел: от -128 до 127.

Аналогично, диапазон значений двухбайтовых целых чисел: -2¹⁵ - +(2¹⁵ -1) (от -32768 до 32767).

Диапазон значений четырехбайтовых целых чисел со знаком: -2³¹ - +(2³¹ – 1) (от -2 147 483 648 до 2 147 483 647)

Сложение и вычитание целых чисел

В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение обратных или дополнительныхкодов уменьшаемого и вычитаемого. Это позволяет существенно упростить конструкцию арифметико-логического устройства процессора.

Сложение обратных кодов. Здесь при сложении чисел А и В имеют место четыре основных и два особых случая:

1. А и В положительные.При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:

Получен правильный результат.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А.Например:

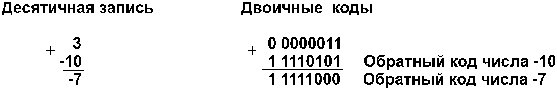
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –7₁₀.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А.Например:

Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицыиз знакового разряда в младший разряд суммы.

4. А и В отрицательные.Например:

Полученный первоначально неправильный результат (обратный код чис­ла –11₁₀вместо обратного кода числа –10₁₀) компьютер исправляет перено­сом единицы из знакового разряда в младший разряд суммы. При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –10₁₀.

Переполнение

При сложении может возникнуть ситуация, когда старшие разряды ре­зуль­тата операции не помещаются в отведенной для него области памяти. Та­кая ситуация называется переполнением разрядной сетки формата числа.Для обнаружения переполнения и оповещения о возникшей ошибке в ком­пью­тере используются специальные средства. Ниже приведены два возмож­ных случая переполнения.

5. А и В положительные, сумма А+В больше, либо равна 2^n–1,где n — количество разрядов формата чисел (для однобайтового формата n=8, 2^n–1= 2⁷= 128). Например:

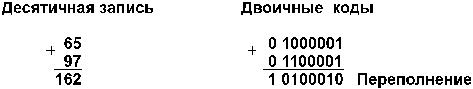
Обратите внимание: в результате сложения положительных чисел полу­чен отрицательный результат!

Семи разрядов цифровой части числового формата недостаточнодля раз­мещения восьмиразрядной суммы (162₁₀= 10100010₂), поэтомустарший разряд суммы оказывается в знаковом разряде.Это вызываетнесов­па­де­ние знака суммы и знаков слагаемых, чтоявляется свидетельством пере­полнения разрядной сетки.

6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2^n–1.Например:

В результате сложения отрицательных чисел полу­чен результат > 0!

Здесь знак суммы тоже не совпадает со знаками слагаемых, что сви­де­тельствует о переполнении разрядной сетки.

Сложение дополнительных кодов.Здесь также имеют место рассмот­рен­ные выше шесть случаев:

1. А и В положительные.Здесь нет отличий от случая 1, рассмотрен­но­го для обратного кода (коды неотрицательных чисел совпадают).

2. А положительное, B отрицательное и по абсолютной величине больше, чем А.Например:

Получен правильный результат в дополнительном коде. При переводе в пря­мой код биты цифровой части результата инвертируются и к младшему раз­ря­ду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –7₁₀.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А.Например:

Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.

4. А и В отрицательные.Например:

Получен правильный результат в дополнительном коде. Единицу пере­носаиз знакового разряда компьютеротбрасывает.

Случаи переполнения

Для обнаружения переполнения разрядной сетки знаковый разряд дуб­ли­руется. Такое представление чисел называетсямодифицированнымдопол­нительным кодом:

1) 65 00 100 0001

⁺ 97⁺ 00 110 0001

162 01 010 0010

Разные цифры в знаковых разрядах свидетельствуют о том, что произошло переполнение.

2) -65 11 011 1111

⁺ -97⁺ 11 001 1111

-162 10 101 1110

Переполнение!

Для проверки знаковых разрядов используют результат операции “ис­клю­­чающее ИЛИ”, которая дает значение 1 только если операнды различны.

Сравнение рассмотренных форм кодирования целых чисел со зна­ком показывает:

на преобразование отрицательного числа в обратный код компью­тер затрачивает меньше времени, чем на преобразование в дополнитель­ный код,так как последнее состоит из двух шагов — образования обратного кода и прибавления единицы к его младшему разряду;

время выполнения сложения для дополнительных кодов чисел мень­ше, чем для их обратных кодов,потому что в таком сложении нет пе­реноса единицы из знакового разряда в младший разряд результата, поэтому для ускорения выполнения расчетов используютдополнительный код.