11. Мезоскопические эффекты в наноэлектронных структурах
11.1.Диффузный и баллистический перенос носителей
вполупроводниках
Для эффектов с пространственными масштабами, занимающими промежуточное место между макроскопическим (как правило, больше 1 мкм) и микроскопическими (порядка размеров атомов и молекул < 1 нм) размерами, существует специальный термин «мезоскопические эффекты». Мезоскопические эффекты проявляются в целом ряде квантово-интерференционных явлений, описание которых выходит за рамки данной книги. В этой главе мы коснемся только нескольких вопросов, имеющих отношение к уже существующим и перспективным наноэлектронным приборам и структурам и представляющих интерес как для физиков, так и для специалистов по электронике.
Для проводников макроскопических размеров выполняется закон Ома, который эквивалентен предположению о том, что средняя дрейфовая скорость носителей пропорциональна электрическому полю внутри проводника:
|
I = V |
|
vdr = μ E = |
q |
τ E . |
(11.1.1) |
|
m |
|
R |
|
|
|
|
Такое соотношение может иметь место, только если набор импульса за счет разгона электронов в электрическом поле уравновешивается за счет потери импульса при множественных столкновениях с примесями и фононами. Такой режим переноса носителей часто называют диффузным, и он выполняется при условии малости длины пробега по импульсу по сравнению с размерами проводникаl<< L, W . Если выполняется обратное неравенство ( l > L), то
такой режим называется баллистическим (бесстолкновительным). Другим необходимым условием справедливости закона Ома является электрическая нейтральность внутри объема проводника. Она позволяет, не решая уравнение Пуассона, считать постоянным электрическое поле E =V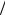
L в проводнике длиной L с приложен-
ным напряжением V . Тогда для двумерного проводника выражение для тока имеет вид
|
I =Wq nS μ E = |
W q2 |
τ |
V = |
V |
, |
(11.1.2) |
|
|
|
|
|
|
L m |
R |
|
|
|
|
|
где W и L – ширина и длина 2D образца:
|
R = |
L m |
. |
(11.1.3) |
|
|
|
|
|
W q2n τ |
|
|
|
|
|
|
|
|
S |
|
|
Глядя на это выражение, можно было бы сделать вывод, что, уменьшая длину проводника, сопротивление можно сделать сколь угодно малым.
R
L
Рис. 11.1. Зависимость сопротивления проводника от его длины
Эксперименты показывают, что сопротивление остается конечным даже при очень малой длине проводника (рис.11.1). При малой длине L перенос носителей через проводник становится баллистическим, а формула (11.1. 3) справедлива только для диффузных проводников. Для баллистического случая длина пробега и времена релаксации не могут входить в выражение для сопротивления. В этих условиях концепция подвижности и коэффициента диффузии теряет свой смысл, и сопротивление транзистора в линейном режиме перестает зависеть от длины канала.
11.2. ВАХ баллистического транзистора
Ток в баллистическом транзисторе можно представить в виде разности потоков электронов, идущих из истока в сток J (+) и из
стока в исток J (−) (рис. 11.2): |
|
IDball = qW (J (+) − J (−)). |
(11.2.1) |
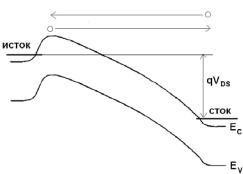
Рис. 11.2. Зонная диаграмма канала МОПТ
Поток из истока в сток J (+) определяется уровнем Ферми и концентрацией nS (0)у истока, поток из стока в исток J (+) определяется концентрацией nS (L) в районе стока:
IDball |
1 qW veff (nS (0)−nS (L)), |
(11.2.2) |
|
2 |
|
где множитель ½ учитывает приближенно, что только половина носителей движется от контактов в сторону канала. Формально более точный множитель 1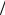
π , что не очень существенно, учитывая
грубость аналитических моделей. Эффективная скорость veff для
баллистического канала соответствует тепловой скорости в невырожденном случае и скорости Ферми для вырожденного случая.
Отношение концентраций носителей в районе стока и истока для невырожденного случая дается формулой (см. п. 9.8)
nS (L) |
|
|
|
|
κ |
|
|
VDS |
|
|
|
|
− |
|
|
|
|
(11.2.3) |
|
|
|
|
|
nS (0) |
= exp |
1 + |
|
|
|
. |
|
|
κ ϕT |
|
Это соотношение получено ранее для диффузного канала, но можно показать, что оно остается справедливым для баллистического случая. Действительно, уравнение непрерывности плотности тока для баллистического пролета в канале транзистора можно записать как условие непрерывности для бесстолкновительного потока
dJ ball |
= |
d |
(n |
(y)v |
|
(y))= 0 |
, |
(11.2.4) |
dy |
dy |
|
|
S |
|
y |
|
|
|
253
где vy (y) – среднее локальное значение компоненты скорости но-
сителя вдоль канала.
Тогда уравнение непрерывности для плотности потока носителей в баллистическом канале запишется как
|
dvy |
=κ |
qE |
v |
y |
, |
|
|
dy |
εD |
|
|
|
|
|
|
|
решение которого имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
κ |
|
|
|
qVDS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vy (L)= vy (0)exp |
1+ |
κ |
|
|
. |
|
|
|
|
|
εD |
Вспоминая интегральную |
форму |
уравнения |
|
непрерывности |
nS (y)vy (y)= const(y), сразу получаем (11.2.3). |
|
|
|
|
|
|
|
|
С учетом (11.2.3) соотношение (11.2.2) приобретает вид |
|
|
1 qWn |
(0)v |
|
|
|
|
|
|
|
κ |
|
|
VDS |
|
(11.2.7) |
I ball = |
1−exp |
− |
|
|
. |
|
|
|
|
D |
2 |
S |
eff |
|
|
|
|
|
|
|
1+κ ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
В линейном омическом режиме, когда VDS |
мало и/или κ <<1, |
получаем в невырожденном случае |
|
|
|
|
)v |
|
|
|
|
|
|
|
|
|
|
I ball |
W (C |
O |
+C |
D |
eff |
V |
DS |
. |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
При относительно больших VDS |
|
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ball |
|
1 qWn |
S |
(0)v . |
|
|
(11.2.8) |
|
|
|
DSAT |
|
2 |
|
|
|
|
eff |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта формула напоминает формулу для тока насыщения (4.16.7) для диффузного канала за одним исключением. Вместо максимальной дрейфовой скорости vSAT в (4.16.7) входит некоторая эффек-
тивная баллистическая скорость veff . Обе скорости по порядку ве-
личины сопоставимы с тепловой скоростью, хотя всегда выполняется неравенство vSAT < veff < vth .
Эффективная баллистическая скорость меньше тепловой за счет того, что некоторая часть носителей рассеивается. Для связи описаний диффузного и баллистического канала введем следующее соотношение:
|
|
|
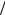
v |
|
|
= |
|
vth |
. |
|
|
|
|
|
|
|
|
|
(11.2.9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eff |
1+ |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По мере того как длина канала увеличивается, мы имеем |
|
|
|
|
veff |
|
|
v |
l |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
th |
|
|
|
= |
n |
. |
|
|
|
|
|
|
(11.2.10) |
|
|
2 |
|
|
2L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
поскольку в двумерной |
|
|
системе |
коэффициент |
диффузии |
Dn = vthl 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда (11.2.7) дает в диффузном пределе L >> l |
|
|
ball |
L>>l |
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
κ VDS |
|
ID |
→ |
|
L |
qDnnS (0) 1−exp |
− |
|
|
|
|
|
|
, |
|
1 |
+κ ϕT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что в точности воспроизводит формулу для ВАХ диффузного МОПТ.
Необходимо подчеркнуть, что физическая граница между диффузным и баллистическим режимом является довольно размытой. Длина пробега носителя по импульсу l, как правило, меньше, чем
длина пробега по энергии lε , и их взаимосвязь определяется соот-
ношением |
|
lε = (2Dnτε )1/ 2 = (vF lτε )1/ 2 . |
(11.2.11) |
Для наноэлектронных транзисторов актуальным является диапазон длин канала от 10 до 70 нм, который подразумевает возмож-
ность реализации неравенства l≤ L ≤ lε . В этом «квази-
баллистическом» режиме остается возможность описания транспорта носителей с помощью коэффициента диффузии и подвижности. Перенос электронов носит упругий диффузный характер с сохранением полной энергии носителя при пролете через канал. Формула (11.2.11) соответствует переходной области между баллистическим и диффузным каналом.
