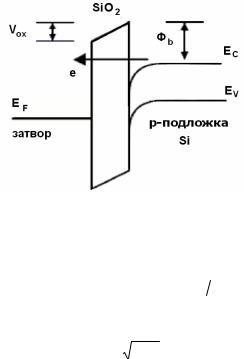
10.3. Прямое туннелирование через подзатворный окисел

Прямое туннелирование через подзатворный окисел n-МОПТ соответствует переходу электронов из зоны проводимости (а может быть и из валентной зоны) кремния непосредственно в затвор (зону проводимости сильнолегированного поликремния или полузаполненную зону металла) (рис. 10.4).

Ток прямого туннелирования из затвора в кремний существенен только для малых толщин подзатворных окислов (< 3…4 нм), типичных для современных приборов. При такой толщине барьера туннельный ток заметен даже при малых электрических полях в окисле и малых смещениях на затворе.

Рис. 10.4. Прямое туннелирование электронов из зоны проводимости Si в зону проводимости SiO2

Строго говоря, ток прямого туннелирования пропорционален вероятности туннелирования через трапециевидный барьер

Экспериментально затруднительно непосредственно соотнести эту формулу с экспериментом, и поэтому на практике часто поль-

230

зуются упрощенным эмпирическим выражением для зависимости плотности прямого туннельного тока через подзатворный изолятор от его толщины в виде

где JG0 = 3.7 × 10-10 пА/мкм2; B0 =9.2 нм-1 для n-МОПТ и JG0 =

3× 10-9 пА/мкм2; B0 =9.9 нм-1для p-МОПТ.

Эта эмпирическая формула соответствует приближению туннелирования через прямоугольный барьер, вероятность которого равна

где U = qΦb ~ 3.1 эВ – эффективная высота потенциального барьера, разделяющего кремниевую подложку и затвор, λ = h2 2mox U – эффективная длина, характеризующая вероят-

ность туннелирования; λ~ 0.1 нм для электронов и приблизительно на 10 % меньше для дырок из-за большего разрыва краев валентных зон кремния и SiO2. Туннельный механизм, который слабо зависит от температуры, особенно важен при относительно низкой температуре, когда остальные механизмы утечек подавлены. Вероятность туннелирования многократно увеличивается, если в окисле есть разрешенное состояние любой природы (атом примеси, дефект любой природы, нарушение структуры решетки с болтающимися связями).

Считается, что допустим такой уровень туннельных токов утечки, при которых они существенно меньше рабочих токов стока, что соответствует плотности туннельных токов 1-10 А/см2 или даже 100 А/см2, хотя при этом туннельные токи будут составлять заметную долю от общего энергопотребления.

Необходимо подчеркнуть, что вероятность туннелирования очень чувствительна к конкретным механизмам туннелирования, к флуктуациям толщины и локального значения высоты потенциального барьера и тонким механизмам деградации структуры окисла, которые не проявляются заметным образом ни в каких других эффектах.

231

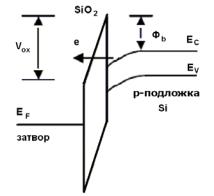
10.4. Механизм Фаулера-Нордгейма

При сильных электрических полях в окисле трапециевидный потенциальный барьер вырождается в треугольный, что приводит к увеличению вероятности туннелирования из зоны проводимости кремния непосредственно в зону проводимости SiO2.

Рис. 10.5. Туннелирование через треугольный потенциальный барьер при механизме Фаулера-Нордгейма

Такое происходит при электрических полях, больших некоторого критического поля Eox(FN ) , при которых падение потенциала в

окисле превосходит высоту барьера между зоной проводимости Si

и SiO2:

Для треугольного потенциального барьера формула для вероятности туннелирования по механизму Фаулера-Нордгейма имеет вид

Формула для плотности тока по механизму Фаулера-Нордгейма имеет вид:

232

ϕB=3.1 эВ (Si-SiO2).

Измеряемый ток Фаулера-Нордгейма невелик даже при очень больших полях (~ 5×10-7 А/см2 при поле 8 МВ/см). Поэтому в нормальном режиме работы транзисторов им можно всегда пренебрегать.

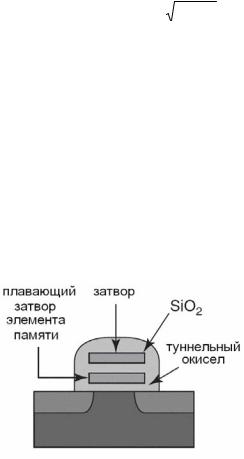
Рис. 10.6. Схема элемента флэш-памяти

Важнейшим применением эффекта Фаулера-Нордгейма является запись информационного заряда в плавающем (изолированном) металлическом затворе элемента флэш-памяти (рис. 10.6).

На практике ток Фаулера-Нордгейма увеличивается на порядок при уменьшении dox приблизительно на один атомный слой, а для тонких окислов – на еще меньшую величину (~2…4 ангстрем). Следует отметить, что разброс в определении толщины окисла в разных методиках может достигать 4 ангстрем.

233