
устройства функциональной электроники-1
.pdf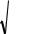
f p = |
1 |
|
|
EЮ |
|
, |
|
2l |
ρ |
||||||
|
|
|
|
|
где l – длина резонатора, ЕЮ – модуль упругости,
ρ - плотность материала.
Точность обработки механических резонаторов должна быть очень высока. Например, для частоты 1 МГц точность обработка достигает 1 мкм. На добротность фильтров оказывает влияние как добротность преобразователей, так и добротность резонаторов и связок. Добротность фильтров с механическими связями достигает 104.
Крутильные колебания имеют на (30-40)% меньшую скорость распространения, поэтому такие фильтры имеют меньший размер. Добротность фильтров с крутильными колебаниями выше, чем фильтров с продольными
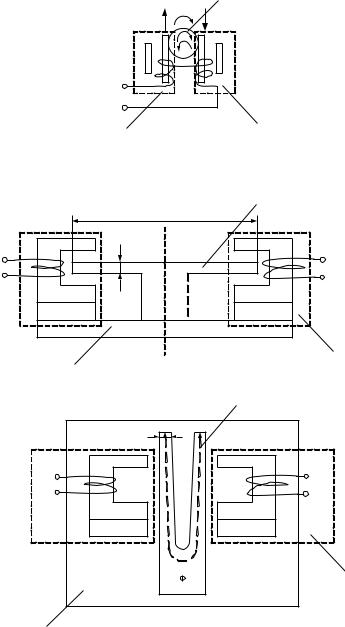
колебаниями. Полоса пропускания составляет (0,3-0,4)% от fp. Для возбуждения крутильных колебаний цилиндрического резонатора необходимо включать два преобразователя, как показано на рис. 1.36. Диски и связки выполняют из термостабильного материала, например, из инвара.
Промышленность выпускает магнитострикционные фильтры ЭМФДП- 9Д-500-8с (500 кГц), ФМЦ-2 (300 кГц) и др. Через обмотки преобразователей не должна протекать постоянная составляющая тока, так как она создает дополнительное магнитное поле, ухудшающее характеристики фильтров. Для защиты фильтров от внешних магнитных полей их помещают в магнитостатические экраны, из пермаллоя или электрохимической стали.
Конструкции фильтров с электромагнитными преобразователями приведены на рис. 1.37 (брусковый резонатор) и 1.38 (камертонный резонатор). Фильтры состоят из механических резонаторов и электромагнитных преобразователей, содержащих магнитный сердечник с обмоткой и постоянный магнит. Электромагнитный преобразователь имеет такую же эквивалентную схему, как и магнитострикционный (рис. 1.30). Брусок и камертон совершают изгибные колебания с резонансной частотой
21
Z |
|
Z1 |
|
|
|
j |
|
|
|
|
Z 1 |
|
0 |
f |
|
|
|
|
|
Z2 |
Полоса |
Полоса |
пропускания |
пропускания |
Рис.1.33
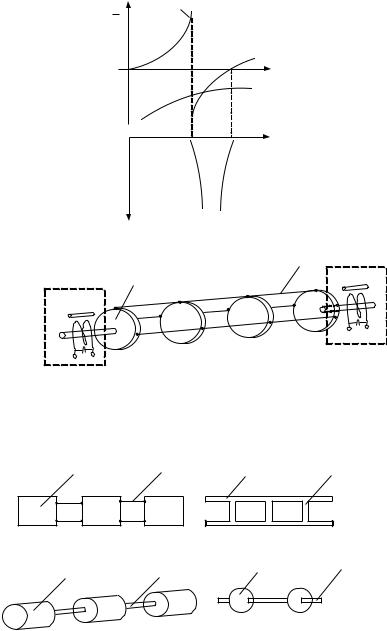
Резонатор
NS
Вх
Магнитострикционный преобразователь
Рис.1.34
Резонатор Связка
а
Резонатор Связка
в
Рис.1.35
Связка
N S
Вых
Резонатор Связка
б
Резонатор Связка
г
22
|
|
|
Резонатор |
|
|
|
S |
N |
|
|
|
N |
S |
|
|
Первый |
|
Второй |
|
|
преобразователь |
преобразователь |
||
|
|
Рис.1.36 |
|
|
|
|
|
Брусковый |
|
|
|
|
резонатор |
|
|
|
l L |
|
|
|
|
t |
|
|
Вх |
|
|
|
Вых |
N |
S |
|
N |
S |
Основание |
|
|
Электромагнитный |
|
|
|
преобразователь |
||
|
|
Рис.1.37 |
Комертонный резонатор |
|
|
|
t |
|
|
Вх |
|
|
|
Вых |
|
N |
S |
N |
S |
|
|
L |
|
|
|
|
|
|
Электромагнитный |
|
|
|
|
преобразователь |
Основание |
|
|
|
|
|
|
Рис.1.38 |
|
|
|
|
23 |
|
|
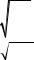
f = 1,07 |
t |
|
|
|
EЮ |
|
. |
l |
2 |
|
|||||
|
|
|
ρ |
||||
Для никеля и его сплавов 
 E
E P ≈ 4.9Ч103 м/с. Такие фильтры на
P ≈ 4.9Ч103 м/с. Такие фильтры на
частоте fр = 1кГц имеют добротность Q = 200-1000.
Расчет электромеханических фильтров изложен в [8]-[11].
1.7. Транзисторные RC-фильтры на конверторах отрицательного сопротивления
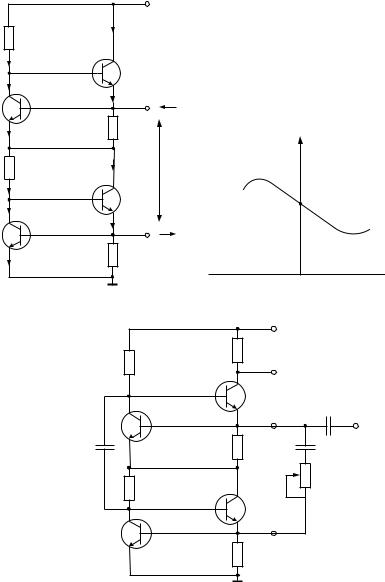
Рассмотрим одну из схем конверторов отрицательного сопротивления, показанную на рис. 1.39. При подаче напряжения питания Е, достаточного для вывода всех транзисторов в активный режим, между клеммами а-б появляется отрицательное дифференциальное сопротивление. Вольтамперная характеристика между клеммами а-б показана на рис. 1.40. С
ростом тока напряжение уменьшается и сопротивление |
Rдиф = |
U |
I |
отрицательно. Примем следующие допущения: все транзисторы имеют одинаковый коэффициент передачи по току в схеме с общей базой, т.е. α1 = α2 = α3 = α4 = α; токи базы много меньше токов эмиттера, поэтому этими точками пренебрегаем; эмиттерно-базовый переход идеален, т.е. при UЭБ = 0,7 В DUЭБ = 0 при росте тока. Рассмотрим малосигнальный случай, т.е. рассмотрим схему в линейном приближении. Обозначим направления приращений токов как показано на рис. 1.39. Тогда, используя законы Кирхгофа, можно составить следующую систему уравнений:
1)DU = DI2 × R1;
2)DU = -DI1 × R1;
3)DI1 = DIК1;
4)DIЭ2 + DI = 0;
5)DIЭ1 = DI2 + DIК4;
6)DI2 = DIК3;
7)DIЭ4 = DI;
8)DIЭ3 = DI1 + DIК2.
Здесь DIаб = DI, DU = DUаб. Объединяя (1) и (2), получим
DU = 0,5R1(DI2 - DI1),
(3)перепишем в виде DI1 = αDIЭ1,
(4)- DIЭ2 = -DI, (5) - DIЭ1 = DI2 + αDIЭ4,
(6) - DI2 = αDIЭ3, (7) - DIЭ4 = DIЭ1 = DI, (8) - DIЭ3 = DI1 - αDI2.
Из (6) IЭ3 = |
I2 |
, из (3) - IЭ1 = |
I1 |
. |
α |
|
|||
|
|
α |
||
24

Тогда (5): |
|
I1 |
= |
I2 + α |
I , |
||
|
α |
||||||
|
|
|
|
|
|
||
А из (6): |
|
|
I2 |
= |
|
I1 − α |
I . |
|
|
|
|
||||
|
|
α |
|
|
|
||
Решая систему из уравнений (5) и (6), получим: |
|||||||
|
|
|
|
I = |
|
α |
2 |
|
I , а |
I |
|
= − |
|
α 2 |
I . |
|
|
|
|||||
|
|
|
|
1+ α |
|
2 |
1+ α |
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Тогда |
подставляя |
|
I1 |
и |
|
I2 в |
уравнение |
для |
U и для |
U на |
I, |
||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
аб |
= |
|
U |
= − |
|
|
α |
2 |
|
R . |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
I |
|
1+ α |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Здесь |
« − |
α |
2 |
» |
называется |
коэффициентом |
конверсии |
КК, |
он |
||||||||||||||
1+ α |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отрицателен. Коэффициент α обычно лежит в пределах 0,9 – 0,999, при таком
изменении α коэффициент конверсии сильно не изменяется, т.е. отрицательное сопротивление относительно стабильно.
Теперь зашунтируем резисторы R1 конденсаторами с емкостью С1. Импеданс такой цепочки
Z1 |
= |
1 |
= |
|
|
1 |
= |
|
|
|
R1 |
|
Y1 |
1 |
+ |
jω C1 |
1 |
+ |
jω C1R1 . |
||||||
|
|
|
R1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Домножим числитель и знаменатель на сопряженное (1+jωC1R1), т.е. на (1-jωC1R1). Получим:
Z1 |
= |
|
R |
|
2 |
− |
jω C R2 |
2 . |
||
1 |
|
1 |
1 |
|||||||
|
|
|
1+ (ω C R ) |
|
|
1+ (ω C R ) |
|
|
||
|
|
1 |
1 |
|
|
1 |
1 |
|
|
|
Если (ωC1R1)2 << 1, то Z1 = R1 - jωC1R12 . Подставим это выражение в Zаб и получим, что
Z |
|
= − |
α 2 |
R + |
α 2 |
jω C R2 . |
|
аб |
1+ α |
1+ α |
|||||
|
|
1 |
1 1 |
Представим Zаб последовательной схемой замещения, состоящей из последовательно соединенных эквивалентной индуктивности LЭ и сопротивления RЭ. Тогда
RЭ = − 1α+ 2α R1 , а LЭ = − 1α+ 2α C1R12 .
Поскольку сопротивление эмиттерного перехода ZЭП → 0, а внутренне сопротивление источника питания равно 0, то е емкости С1 включаются параллельно и дают емкость 2С1, включенную между базами транзисторов VT2 и VT4. Если обозначить 2С1 как С1, то параллельно R1 должны
25

включаться емкости C21 . С учетом этого
LЭ = 0,51α+ 2α C1R12 .
Таким образом, между клеммами а-б имеется цепочка из LЭ и RЭ. Подключим параллельно клеммам а-б цепочку из последовательно соединенных конденсатора С2 и резистора переменного сопротивления R3. Получим параллельный колебательный контур. Сигнал в него будем вводить через конденсатор С3 (С3<<С2) или резистор с большим сопротивление. Так как в параллельном контуре наблюдается резонанс токов, то включив сопротивление нагрузки (малое) R4 в цепь коллектора транзистора VT2, получим полосовой фильтр, изображенный на рис. 1.41 (эквивалент колебательного контура).
Температурный коэффициент
α LЭ = α KK + 2α R1 + α C1 . Так как резонансная частота контура
|
|
|
|
|
|
fp |
= |
|
|
1 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2π |
|
LС |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Э |
|
|
|
|
|
|
|
|
то |
α |
f |
= − 0,5(α |
LС |
+ α |
) = − 0,5(α |
|
|
+ |
2α |
C |
+ α |
C |
+ α |
|
) |
. |
|||
|
pЭ |
|
2 |
|
К |
1 |
R |
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|||||
Зная величину и знак α KH , α R1 и выбрав знак и величину α C1 и α C2 ,
можно добиться того, чтобы α fP стремился к 0, т.е. возможна термокомпен-
сация частоты контура.
В схеме резистор R3 служит для компенсации отрицательного сопротивления RЭ (в противном случае получается генератор синусоиды).
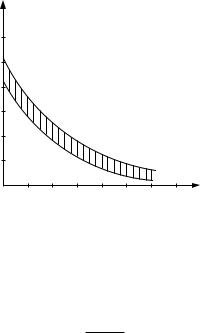
При заданной частоте fр и использовании маломощных транзисторных сборок типа К1НТ591В сопротивление R1 рекомендуется выбирать, пользуясь графиком рис. 1.42. Этот график является результатом
эксперимента. Емкость |
C = 0,2 − |
0,6 |
, |
R = (0,5 − |
2)Uаб R |
, |
||||||||||||||
|
1 |
π |
f |
|
R |
|
2 |
|
|
|
Е − |
1 |
||||||||
|
|
|
P |
|
|
|
|
|
|
4Uаб |
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
C3 |
= |
C2 |
|
|
|
, |
C2 |
= |
|
1 |
|
|
|
. |
|
|
||||
(30 |
− |
50) |
40 f |
2 |
L |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Потребляемая мощность |
|
|
|
|
|
|
|
|
|
|
PЭ |
|
|
|
|
|||||
ж |
|
|
|
|
|
|
|
UЭП ц |
|
|
|
|
||||||||
|
|
|
P = |
0,5E − |
2UЭП |
+ |
E |
|
|
|||||||||||
|
|
|
з |
|
|
|
|
|
|
|
|
|
ч |
, |
|
|||||
|
|
|
|
|
|
R |
|
|
|
R |
|
|
||||||||
|
|
|
|
и |
|
|
|
1 |
|
|
|
|
2 |
|
ш |
|
|
|
|
|
где для кремниевых транзисторов UЭП = 0,7 В, Е=(4-15)В. Добротность фильтра регулируется резистором R3, с ростом уровня
переменного сигнала (выше 20 мВ) она уменьшается. Величина добротности Q = (10÷70), потребляемая мощность Р=(0,1÷30)мВт. Фильтры легко
26
реализуются методами микроэлектроники. Другие варианты фильтров приведены в [12], [13]. Их рабочие частоты достигают 360 МГц.
|
|
|
+E |
|
R1 |
∆IК2 |
|
|
|
|
|
|
|
|
∆I1 |
|
|
|
|
∆IК1 |
VT2 |
|
|
|
∆I Э2 |
a |
|
|
|
VT1 |
∆I-аб |
|
||
|
|
|
|
|
∆I Э1 |
R2 |
|
|
U аб |
|
|
|
||
R1 |
∆IК4 |
|
∆U аб |
|
∆I2 |
VT4 |
|
|
0.5E |
∆IК3 |
|
|
||
∆I Э4 |
б |
|
|
|
VT3 |
∆Iаб |
|
||
|
|
|
|
|
∆I Э3 |
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Рис.1.39 |
|
|
Рис.1.40 |
|
|
|
|
+E |
|
R1 |
R4 |
|
|
|
|
Вых |
||
|
|
|
|
|
|
|
|
VT2 |
C3 |
|
|
|
VT1 |
|
|
|
|
a |
|
|
C1 |
|
R2 |
C2 |
|
|
|
|
R3 |
|
R1 |
|
|
|
|
|
|
VT4 |
|
|
|
|
VT3 |
б |
|
|
|
R2 |
|
 I аб
I аб
Вх
Рис.1.41
27
R1 |
|
|
|
|
|
|
Ом |
|
|
|
|
|
|
10 8 |
|
|
|
|
|
|
10 7 |
|
|
|
|
|
|
10 6 |
|
|
|
|
|
|
10 5 |
|
|
|
|
|
|
10 4 |
|
|
|
|
|
|
10 3 |
|
|
|
|
|
|
102 |
10 3 |
10 4 |
105 |
106 |
10 7 |
f p,Гц |
108 |
Рис.1.42
1.8. Конверторный фильтр на операционном усилителе
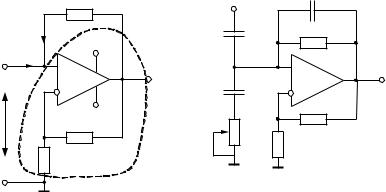
Схема конвертора отрицательного сопротивления (КОС) на операционном усилителе (ОУ) показана на рис. 1.43. Рассмотрим напряжения на выходе ОУ U0= UКЭ, где КЭ – эквивалентный коэффициент передачи ОУ с учетом элементов отрицательной обратной связи. Из теории усилителей с
обратной связью известно, что KЭ = K K , где K – коэффициент усиления
1+ β
по напряжению ОУ (собственный коэффициент усиления), β - коэффициент обратной связи, показывающий, какая часть выходного напряжения подается
на вход, |
β = |
|
R3 |
. Ток положительной обратной связи (приращение тока) |
|||||
R2 |
+ R3 |
||||||||
|
|
|
|
|
U0 |
|
|||
|
|
|
|
I0 |
= |
|
, |
||
|
|
|
|
R1 |
|
||||
|
|
|
|
|
|
+ Zвх |
|||
где Zвх – входное сопротивление усилителя.
Пренебрегая входным сопротивлением собственно ОУ, получим:
Тогда |
|
|
|
|
|
|
|
|
I0 = - |
I. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
+ Zвх ) ж |
|
|
|
|
|
|
|
|
|
ц |
|
|
|||
UК= |
U |
0 |
= − |
I(R1 |
+ Zвх ) |
= − |
|
I (R1 |
+ |
|
|
|
|
R3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
з1 |
|
|
|
|
|
|
|
|
ч . |
|
|
|||||
KК |
|
|
К |
|
|
|
R |
|
|
|
|
+ |
|
|
|
|
|
|||||||||
|
|
|
Э |
|
|
|
|
|
|
R |
|
|
|
2 |
|
3 |
|
ш |
|
|
||||||
|
Э |
|
|
|
|
|
|
|
|
|
|
|
и |
ж 1 |
|
|
|
|
ц |
|||||||
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
R3 |
|
|||||
Сопротивление Zаб = Zвх = |
|
|
|
= − (R1 |
+ Zвх )з |
|
|
|
+ |
|
|
|
|
|
ч . |
|||||||||||
|
|
|
|
|
|
|
|
+ |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
IК |
R |
R |
и |
|
|
|
|
2 |
3 ш |
|||||||
28
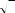
|
|
|
|
1 |
|
+ |
|
|
R3 |
|
|
|
|
|
|
Zвх = − R1 |
|
K |
|
|
R + R |
|
|
|
|||||
Отсюда |
|
|
|
|
|
|
|
2 |
3 |
. |
||||
|
|
|
1 |
|
|
R3 |
|
|||||||
|
1+ |
|
|
+ |
|
|
|
|
||||||
|
|
K |
R + |
R |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
Так как K >> 1, R3 << R2, |
|
R3 |
< < 1 |
, |
|
R |
+ R |
||||
|
|
|
|||
|
2 |
3 |
|
|
|
|
|
Zвх = |
− R1 |
R2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Если зашунтировать резистор R1 конденсатором с емкостью С1, то |
|||||||||||||||
при (ωС1R1)2 << 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zвх = − |
R3 |
(R1 |
− jω C1R12 ) = − |
R3 |
R1 + jω C1R12 |
R3 |
= RЭ + jω LЭ . |
|
|
||||||
R |
R |
R |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
2 |
|
|
|
2 |
|
R3 |
|
|
R3 |
|
|||
Отсюда в последовательной схеме замещения |
R = − |
|
R L = − |
C R2 |
|||||||||||
|
|
|
|||||||||||||
Э |
1 , |
Э |
1 1 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
R2 |
||
Схема полосового фильтра на таком КОС приведена на рис. 1.44. Она построена так же, как и в предыдущем подразделе. Такие фильтры очень низкочастотны. Эту же схему можно рассматривать как отрицательный инвертор сопротивления с коэффициентом инверсии КИ = R1R3. Тогда
Zвх = − КН .
R2
Теперь если шунтировать конденсатором с емкостью С1 резистор R2, то на входе получим последовательное соединение эквивалентного активного
сопротивления RЭ = − R1 |
R3 |
|
и отрицательной индуктивности LЭ = -R1R3C1. |
||||||||||||||||
|
|||||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
||
Все выводы справедливы, если K = 104-106, а |
= 10− 1 − 10− 2 , что обычно |
||||||||||||||||||
R |
|||||||||||||||||||
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|
2 |
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и наблюдается. Но если |
|
и |
|
|
|
|
|
сравнимы между собой, но много |
|||||||||||
|
R + |
R |
|
||||||||||||||||
K |
|||||||||||||||||||
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
меньше 1, то из формулы для Zвх следует, что |
|
|
|
|
|
||||||||||||||
|
|
|
|
Zвх = − R1 |
ж |
1 |
+ |
|
R3 |
ц |
|||||||||
|
|
|
|
з |
|
|
|
|
|
ч . |
|||||||||
|
|
|
|
K |
|
R |
|||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
2 |
ш |
|||||||
С учетом того, что частотная зависимость коэффициента К |
|||||||||||||||||||
аппроксимируется формулой |
|
|
|
|
|
|
|
K0 |
|
|
|
|
|
||||||
|
|
|
|
|
K = |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1+ |
|
j |
|
f , |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
fгр |
|
|
|||||||||
где K0 – низкочастотное значение коэффициента К,
fгр – частота, на которой К уменьшается в 
 2 , граничная частота.
2 , граничная частота.
29
R1 |
Вх |
C1 |
|
|
|
||
|
C3 |
R1 |
|
|
|
|
|
a |
|
|
|
+ |
|
+ |
∆U0 Вых |
К |
|
ОУ |
|
- |
C2 |
- |
|
|
|
R2 |
|
∆U |
R4 |
|
|
|
R3 |
|
|
|
|
|
|
К |
Э |
|
|
б |
|
|
|
Рис.1.43 |
|
Рис.1.44 |
|
Тогда
|
ж |
1+ |
j |
|
f |
|
|
ц |
|
з |
|
|
|
|
ч |
||
|
|
fгр |
|
R |
||||
Zвх = − R1 |
з |
|
|
|
|
+ |
3 |
ч . |
|
К0 |
|
R2 |
|||||
|
з |
|
|
|
ч |
|||
|
з |
|
|
|
|
|
|
ч |
|
и |
|
|
|
|
|
|
ш |
Представляя Zвх как параллельное соединение RЭ и СЭ, из этого выражения получим, что
|
|
|
1 |
|
= − |
|
а |
|
|
, |
СЭ |
= |
|
|
|
в |
|
Ч |
1 |
|
, |
||
|
|
|
|
|
|
2 |
+ |
|
2 |
|
а |
2 |
+ в |
2 |
2π |
f |
|||||||
|
|
RаЭ |
в |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где |
a = R |
ж |
1 |
+ |
R3 |
ц |
, |
в = |
R1 f |
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
з |
|
|
|
ч |
fК |
|
|
|
|
|
|
|
|
||||||||||
|
1 |
K0 |
|
R2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
и |
|
ш |
|
|
|
гр |
|
|
|
|
|
|
|
|
|
|||||
Расчеты и эксперимент показывают, что емкость СЭ очень высокая (десятки – сотни) пФ.
1.9. Гираторные полосовые фильтры на транзисторах
Один из вариантов гираторных фильтров на транзисторах показан на рис 1.45 [14]. Здесь имеется два усилителя (транзисторы VT2 и VT4) с динамическими нагрузками (транзисторы VT1 и VT5). Связь с выхода первого усилителя на вход второго непосредственная, а с выхода второго на вход первого – через эмиттерный повторитель (VT3). Емкость конденсатора С1 инвертируется в эквивалентную индуктивность между клеммами а-б. Чтобы сопротивление нагрузки не сильно влияло на параметры контура, состоящего из эквивалентной индуктивности меду клеммами а-б и емкости конденсатора С2, применен эмиттерный повторитель на транзисторе VT6.
Полагая, что все транзисторы имеют одинаковый коэффициент передачи по току в схеме с общей базой α, R5 >> RН, R6 >> R4 можно записать
30
