2.3. Определение координат складов относительно «центра тяжести»

1) Найденные координаты склада, при которых достигается минимальное значение целевой функции принять в качестве координат центра тяжести.

2) Определить расстояние между координатами максимально удаленных друг от друга пунктов

₍₈₎

₍₉₎

где x_i, x_j – координаты поставщиков;

y_i, y_j – координаты потребителей.

3) Выбрать минимальное расстояние и определить радиус окружности R, на которой диаметрально располагаются склады:

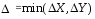₍₁₀₎

₍₁₁₎

4) Рассчитать величину грузооборота при различном расположении складов относительно окружности (горизонтальное и вертикальное), а также при различных радиусах окружности R (R=0,1Δ; R=0,2Δ; R=0,3Δ и т.д.). Для целей курсового проекта расчеты произвести для двух вариантов радиусов R=0,2Δ и R=0,5Δ и варианта с двумя складами (k=2):

₍₁₂₎

где i=(1,…,m) – поставщики;

k=(1,…,l) – склады;

j=(1,…,n) – потребители;

L_ik, L_kj – расстояние от i-го поставщика до k-го склада и от k-го склада до j-го потребителя соответственно;

Q_ik, Q_kj – объемы перевозок грузов от i-го поставщика до k-го склада и от k-го склада до j-го потребителя соответственно;

W_ik, W_kj – произведение весовых долей i-го поставщика и k-го склада, k-го склада и j-го потребителя.

5) Рассчитать суммарные затраты на транспортировку для различных вариантов:

₍₁₃₎

6) Результаты расчетов представить в табличном виде (таблица 3). Выявить вариант решения, обеспечивающих выполнение условия:

₍₁₄₎

Таблица 3 – Определение рационального расположения складов

Расположение складов	Радиус	Величина транспортных расходов, у.е. при количестве складов
		нет	2 склада
Горизонтальное	0,2Δ
Вертикальное
Горизонтальное	0,5Δ
Вертикальное

2.4. Корректировка полученных результатов

1) Произвести верификацию расположения складов (по выбранному варианту) на географическом пространстве региона. С учетом выполненной корректировки мест(а) расположения региональных(ого) складов(а) представить расчет суммарных затрат на транспортировку;

2) Произвести корректировку затрат на транспортировку. Для этого:

а) Определить величину оптимальной партии отправки для поставщиков и региональных складов по формуле:

(15)

где А – потребность в продукции в течение рассматриваемого периода;

С₀ – затраты на выполнение одного заказа;

С_п – цена единицы продукции;

f – доля от цены С_п, приходящаяся на затраты по хранению.

б) Определить требуемую грузоподъемность (грузовместимость) транспортных средств;

в) Определить тарифы на перевозку;

г) Откорректировать величину затрат на транспортировку по рассмотренным ранее вариантам.

3. Определение количества и местоположения филиальных (подсортировочных) складов

3.1.Подготовка исходных данных для формирования математической модели транспортно-складской задачи

Для этого:

1) на основе анализа транспортной системы региона, дислокации объектов складской инфраструктуры выбрать потенциальные места расположения филиальных складов компании. Для первой итерации принять количество филиальных складов m=5;

2) произвести первоначальное закрепление потребителей продукции за филиальными складами (таблица 4)

Таблица 4 – Закрепление потребителей за филиальными складами

Потребители	Филиальные склады (ФС)						Объемы поставок, т		Количество груженых ездок
	ФС № 1	ФС № 2	ФС № 3	…	ФС № М
Итого

3) определить среднюю величину оптимальной партии отправки для филиальных складов, пользуясь формулой (15). Выбрать подвижной состав, определить количество груженых ездок по формуле (4), результаты занести в таблицу 4.

4) составить таблицу затрат (таблица 5) на доставку грузов от каждого филиального склада до потребителя с учетом выбранного типа подвижного состава:

₍₁₆₎

где - тариф за доставку грузов автомобильным транспортом выбранного типа транспортных средств, руб./км пробега;

- расстояние от j-го филиального склада до i-го потребителя.

3.2. Формирование математической модели транспортно-складской задачи для определения количества и местоположения филиальных складов.

Таблица 5 – Затраты на доставку грузов автомобильным транспортом

Потребители	Филиальные склады (ФС)
	ФС № 1	ФС № 2	ФС № 3	…	ФС № М
Итого

Общий вид модели транспортно-складской задачи при определении рационального количества филиальных складов:

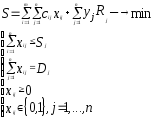(16)

где x_ij – количество отправок со склада (здесь – количество автомобилей, отправляемых со склада);

с_ij – средние транспортные издержки на отправку одного автомобиля со склада j потребителю i (здесь - тариф на доставку грузов от каждого филиального склада j до потребителя i, см. табл.5);

S_j – пропускная способность j-го филиального склада (для первой итерации принять значения, существенно превышающие величину отправки с j-го склада);

D_i – спрос i-го потребителя;

R_j – постоянные затраты, связанные с содержанием или арендой склада;

y_j - двоичная переменная решения (y_j=1, если склад используется в решении; y_j=0, если склад не используется в решении).

Формирование математической модели рекомендуется выполнить с использованием табличного процессора MS Office Excel.