3.1. Методы оценки привлекательности инвестиций

Метод определения чистой текущей стоимости. Метод оценки инвестиций, основанный на определении чистой текущей стоимости, заключается в определении разницы между суммой денежных поступлений дисконтированных к текущей их стоимости и суммой дисконтированных текущих стоимостей всех затрат, необходимых для реализации оцениваемого проекта.

где:

k – желаемая норма прибыльности (рентабельности), процентная ставка;

I_t – инвестиционные затраты в период t;

CF_t -поступление денежных средств в конце периода t.

Если реализация проекта предполагает разовое вложение средств, то следует использовать следующую формулу:

, где:

I₀ – первоначальная сумма вложенных средств;

Если чистая текущая стоимость проекта NPV положительна, то это означает, что в результате реализации такого проекта ценность фирмы возрастет, а проект может быть принят и наоборот.

Метод расчета рентабельности инвестиций. Рентабельность инвестиций PI – показатель, позволяющий определить, в какой мере возрастает ценность фирмы при реализации проекта в расчете на 1 руб. инвестиций. Расчет показателя рентабельности производится по формуле:

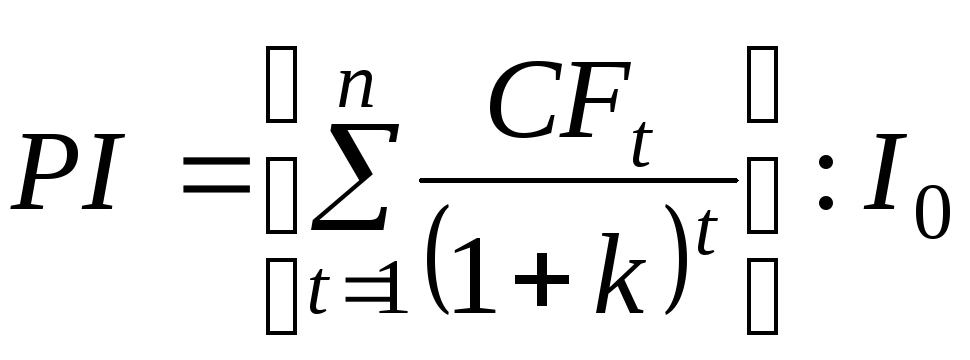, где:

I₀ – первоначальные инвестиции;

CF_t – денежные поступления в году t, которые будут получены благодаря этим инвестициям.

Аналогично методу определения чистой текущей стоимости, в случае, если реализация проекта предусматривает не однократное инвестирование, необходимо все инвестиционные затраты привести к текущей стоимости, используя формулу:

, где:

I_t – инвестиции в году t.

Значение показателя PI, являющееся больше единицы, свидетельствует о приемлемости такого инвестиционного проекта.

Метод расчета внутренней нормы прибыли. Внутренняя норма прибыли IRR, или внутренний коэффициент окупаемости, представляет собой, по существу, уровень окупаемости средств, направленных на цели инвестирования, и по своей природе близок к различного рода процентным ставкам. Фактически внутренняя норма прибыли характеризует максимальный уровень затрат, которые могут иметь место при реализации конкретного инвестиционного проекта и обеспечивать его безубыточность.

Из сказанного ясно, что IRR – это такое значение k, при котором NPV равна нулю.

Для определения значения IRR по проекту, необходимо решить следующее уравнение относительно k:

,

Решение этого уравнения можно упростить, применив формулу:

, где:

k₁, k₂ – такие коэффициенты дисконтирования, при которых NPV изменяет знак с «+» на «–» или наоборот.

IRR сравнивают с тем уровнем окупаемости вложений, который фирма (инвестор) выбирает для себя в качестве стандартного. Этот стандартный уровень желательной рентабельности вложений называют барьерным коэффициентом HR.

Принцип сравнения этих показателей:

• если IRR > HR – проект приемлем;

• если IRR < HR – проект неприемлем;

• если IRR = HR – можно принимать любое решение.

Метод расчета периода окупаемости инвестиций. Метод расчета периода (срока) окупаемости PP инвестиций состоит в определении того срока, который понадобиться для возмещения суммы первоначальных инвестиций. Метод предполагает вычисление того периода, за который кумулятивная сумма денежных поступлений сравняется с суммой первоначальных инвестиций. Формула расчета периода окупаемости имеет вид:

, где:

PP – период окупаемости (лет);

I₀ – первоначальные инвестиции;

CF_t^() – годичная сумма денежных поступлений от реализации инвестиционного проекта.

Индекс  при знаменателе СF_t говорит о возможности двоякого подхода к определению величины СF_t.

Первый подход возможен в том случае, когда величины денежных поступлений примерно равны по годам. Тогда сумма первоначальных инвестиций делится на величину годовых (среднегодовых) поступлений.

Второй подход предполагает расчет величины денежных поступлений от реализации проекта нарастающим итогом, т.е. как кумулятивной величины.

Если период окупаемости рассчитывается на основе нарастающей суммы денежных поступлений, то может возникнуть ситуация, когда срок накопления суммы, равной первоначальным инвестициям, не кратен целому числу лет. Чтобы определить в такой ситуации точный период окупаемости инвестиций, надо:

Найти кумулятивную сумму денежных поступлений за целое число периодов, при котором такая сумма оказывается наиболее близкой к величине инвестиций, но меньше ее;

Определить, какая часть суммы инвестиций осталась еще непокрытой денежными поступлениями;

Поделить этот непокрытый остаток суммы инвестиций на величину денежных поступлений в следующем целом периоде, чтобы определить, какую часть остаток составляет от этой величины. Полученный результат будет характеризовать ту долю данного периода, которая в сумме с предыдущими целыми периодами и образует общую величину периода окупаемости.

Задание. По прогнозным оценкам инвестиционный проект компании стоимостью I₀ рублей будет приносить доходы в течение нескольких ближайших лет. В конце каждого года компания планирует получить доход в размере CF_n. Определите чистую текущую стоимость, рентабельность, внутреннюю норму прибыли и период окупаемости инвестиционного проекта, при годовой процентной ставке k.

3.2. Метод определения бухгалтерской рентабельности инвестиций. Показатель бухгалтерской рентабельности инвестиций ROI ориентирован на оценку инвестиций на основе бухгалтерского показателя – дохода фирмы.

Он представляет собой отношение средней величины дохода фирмы до процентных и налоговых платежей (EBIT) или после налоговых, но до процентных платежей по бухгалтерской отчетности к средней величине инвестиций.

Величину инвестиций, по отношению к которой определяется рентабельность, находят как среднее между учетной стоимостью активов С_а на начало и конец рассматриваемого периода. Формула расчета бухгалтерской рентабельности инвестиций после налоговых отчислений имеет вид:

, где:

H – ставка налогообложения;

C_a – учетная стоимость активов на начало и конец периода оценки.

Применение показателя ROI основано на сопоставлении его расчетного уровня со стандартными для фирмы уровнями рентабельности.

Задание. Стоимость активов компании на начало периода составляла =900000 рублей, а на конец – =0 рублей. Определите бухгалтерскую рентабельность инвестиций, если доход, полученный от реализации инвестиционного проекта, связанного с увеличением активов компании, составляет Д=16000 рублей, а ставка налога – Н =28%.

Упражнение 4: Инвестиционная оценка долговых ценных бумаг

4.1 Оценка облигаций с нулевым купоном. Поскольку по облигациям с нулевым купоном денежные поступления по годам, за исключением последнего года, равны нулю, формула имеет вид:

,

где:

V_t – стоимость облигации с позиции инвестора (теоретическая стоимость);

CF_n – сумма, выплачиваемая при погашении облигации;

n – число лет, через которое произойдет погашение облигации.

Задание 4.1. Облигация нарицательной стоимостью CF_n=2000 , с нулевым купоном продаются за P=1000 рублей. Облигация будет погашена через n=5 лет. Рассчитайте теоретическую стоимость облигации, если альтернативный инвестиционный проект обеспечивает доходность на уровне k=13% и примите решение относительно целесообразности инвестиций в данный вид долговых обязательств.

4.2. Оценка бессрочных облигаций. Бессрочная облигация предполагает неопределенно долгую выплату дохода (CF) в установленном размере (перпетуитет). В этом случае ее оценка осуществляется по формуле:

.

Задание. Определить теоретическую стоимость бессрочной облигации с годовым доходом CF=150руб. и рыночной нормой прибыли k=16%.

4.3. Оценка безотзывных облигаций с постоянным доходом. В этом случае доход от инвестиций в облигацию складывается из одинаковых по годам поступлений (CF) и нарицательной стоимости облигации (CF_n), выплачиваемой в момент погашения:

.

Задание. Определить теоретическую стоимость безотзывной облигации с постоянным доходом, если ее нарицательная стоимость CF_n=1000, купонная ставка составляет r=12% процентов, а рыночная норма прибыли (коэффициент дисконтирования) – k=10%. Срок обращения облигации составляет 6 лет.

4.4. Оценка отзывных облигаций с постоянным доходом. Отзывная облигация отличается от безотзывной наличием выкупной цены и срока защиты от досрочного погашения.

Оценка подобных облигаций осуществляется с использованием формулы оценки безотзывных облигаций, в которой нарицательная стоимость заменяется выкупной ценой – Р_с.

Задание. Определить теоретическую стоимость отзывной облигации с постоянным доходом, если ее нарицательная стоимость CF_n=500руб_., купонная ставка составляет r=10% процентов, а рыночная норма прибыли (коэффициент дисконтирования) – k=8%. Срок обращения облигации составляет n=5 лет. Защита от досрочного отзыва на момент анализа составляет 3 года.

Упражнение 5: Инвестиционная оценка долевых ценных бумаг

5.1. Оценка привилегированных и обыкновенных акций. Теоретическая стоимость привилегированной акции рассчитывается, как и бессрочных облигаций.

Если эмитированные привилегированные акции выкупаются по соответствующей цене, называемой ценой выкупа, то, в этом случае, текущая теоретическая стоимость таких акций определяется также как безотзывных облигаций, где CF_n заменяется ценой выкупа Р_с.

Для оценки обыкновенных акций применяется метод, основанный на оценке их будущих поступлений.

Задание. Определите текущую теоретическую стоимость привилегированной акции, если размер дивидендов в год составляет – 300 рублей, цена выкупа в конце пятого года составляет 1700 рублей, а рыночная норма прибыли для подобного рода активов составляет – 12%.

5.2. В случае с обыкновенными акциями в зависимости от предполагаемой динамики дивидендов базовыми являются три варианта:

• дивиденды не меняются (ситуация аналогична ситуации с привилегированными акциями);

• дивиденды возрастают с постоянным темпом прироста;

• дивиденды возрастают с изменяющимся темпом прироста.

Оценка акций с равномерно возрастающими дивидендами. Если принять за C величину последнего выплаченного дивиденда, а за g – годовой темп прироста, то дивиденд за очередной год составит: С·(1+g) и каждый последующий год будет увеличиваться в (1+g) раз. Если число лет, в которых прогнозируется выплата постоянно возрастающего дивиденда достаточно велико, то формула для оценки акций с равномерно возрастающими дивидендами имеет вид:

.

Данная формула имеет смысл при k>g и называется моделью Гордона.

Задание. Величина последнего выплаченного дивиденда составляет 100 рублей. Темп прироста дивиденда 4 % в год. Рыночная норма прибыли для акций данного класса составляет 16% в год. Определите текущую теоретическую стоимость акции.

5.3. Оценка акций с изменяющимся темпом прироста. На практике фактически не существует ситуаций равномерного постоянного увеличения размера дивиденда. Поэтому для осуществления корректных расчетов интервал прогнозирования разбивают на подинтервалы, характеризующиеся индивидуальным темпом прироста. Так, если выделить два подинтервала с различными темпами прироста, то расчетная формула примет следующий вид:

, где:

C₀ – дивиденд, выплаченный в базисный момент времени;

C_n – прогноз дивиденда в n-ом периоде;

g – прогноз темпа прироста дивиденда в первые n периодов;

p – прогноз темпа прироста дивидендов в последующие периоды.

Решение такого рода задач по сути аналогично заданию 5.2. с оговоркой о разбиении срока обращения (владения) акцией на подинтервалы с учетом изменчивости темпа прироста дивидендов.

В теории и практике оценки акций также рассматривается ситуация, когда темп прироста дивидендов в течение нескольких лет меняется, а по их истечении стабилизируется или равномерно изменяется.

Формула, позволяющая рассчитать теоретическую стоимость акции с такой тенденцией изменения дивидендов, имеет следующий вид, где первое слагаемое представляет собой сумму дисконтированных дивидендов, полученных в периоды их непостоянства, а второе слагаемое основано на модели Гордона и учитывает постоянство темпа прироста дивидендов:

, где:

V_t – показатель оценки акции;

n – продолжительность фазы непостоянного роста, лет;

С_j, где: j = 1,2,.., n – дивиденды в этот период по годам;

С_n+1 — первый ожидаемый дивиденд фазы постоянного роста с темпом g;

k – приемлемая норма прибыли.

Задание. Компания-эмитент планирует выплачивать в ближайшее время дивиденды в размерах, указанных в таблице. Впоследствии темп прироста дивиденда будет постоянным, он также указан в таблице. Рыночная норма прибыли для акций такого класса составляет 16%.

Размер дивидендов, выплаченных в конце…, рублей					Прогнозируемый темп прироста дивидендов, g,%
1 года	2 года	3 года	4 года	5 года
245	220	200	210	230	7

Упражнение 6: Оценка доходности финансовых активов

Показатели доходности входят в группу показателей эффективности использования финансовых активов. Показатели доходности являются относительными и в наиболее общем виде могут быть представлены соотношением дохода (D), генерируемого финансовым активом и величиной инвестиций (СI) в этот актив:

.

При известной базовой цене финансового актива и прогнозируемых доходах и будущей цене актива для расчета доходности следует решить уравнение текущей теоретической стоимости финансового актива относительно параметраk. Полученное значениеkможно трактовать как общую доходность данного актива.

6.1. Доходность облигации без права досрочного погашения. Доходность облигации без права досрочного погашения фактически является доходностью к погашению и обозначается YTM.

Доходность такой облигации может быть определена с помощью формулы оценки безотзывных облигаций, если искомой величиной будет процентная ставка.

Приблизительная оценка стоимости подобной облигации может быть выполнена по формуле:

, где:

C – купонный доход;

M – номинал облигации;

P – текущая цена (на момент оценки);

n – число лет, оставшихся до погашения облигации.

Задание . Рассчитать доходность облигации нарицательной стоимостью - 1000 рублей с купонной ставкой 11%, имеющей текущую рыночную цену 900 рублей. Облигация будет принята к погашению через 3 года.