Пусть непрерывная случайная величина Х задана |
||||
функцией распределения |
|
|
||
|
0, |
x 0 |
||
F(x) |
e |
x |
, |
x 0 |
1 |
|
|||
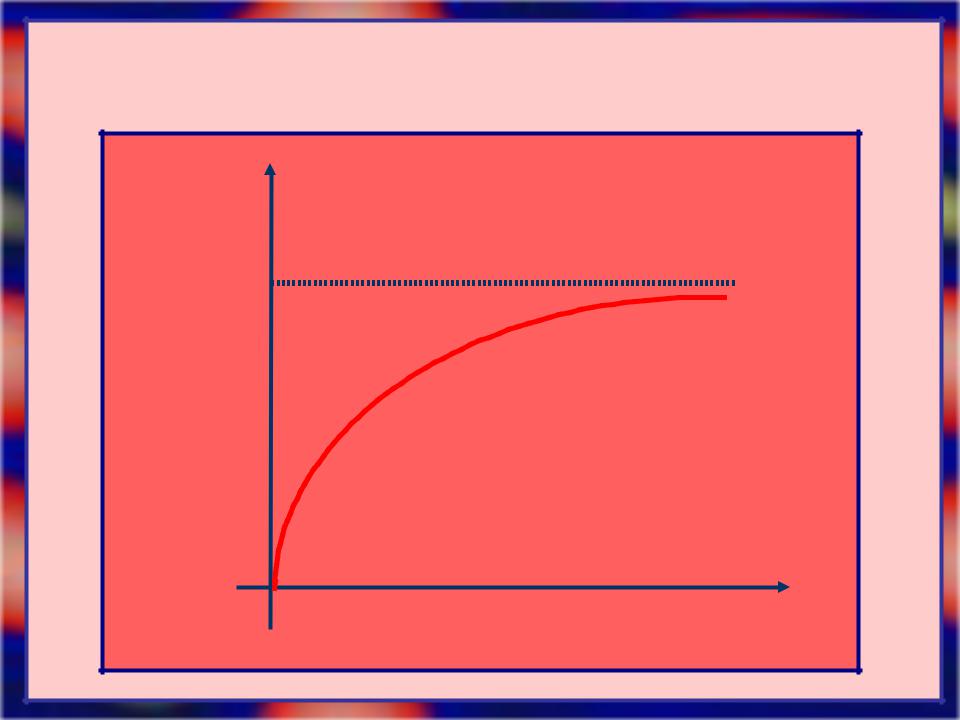
График функции распределения имеет вид: |
F(x) |
1 |
x |
Найдем плотность вероятности этой случайной |
||||
величины. |
|
|
|
|
Плотность вероятности находится как |
||||
производная от функции распределения: |
||||
|
0, |
|
x 0 |
|
f (x) |
e |
x |
, |
x 0 |
|
|
|||
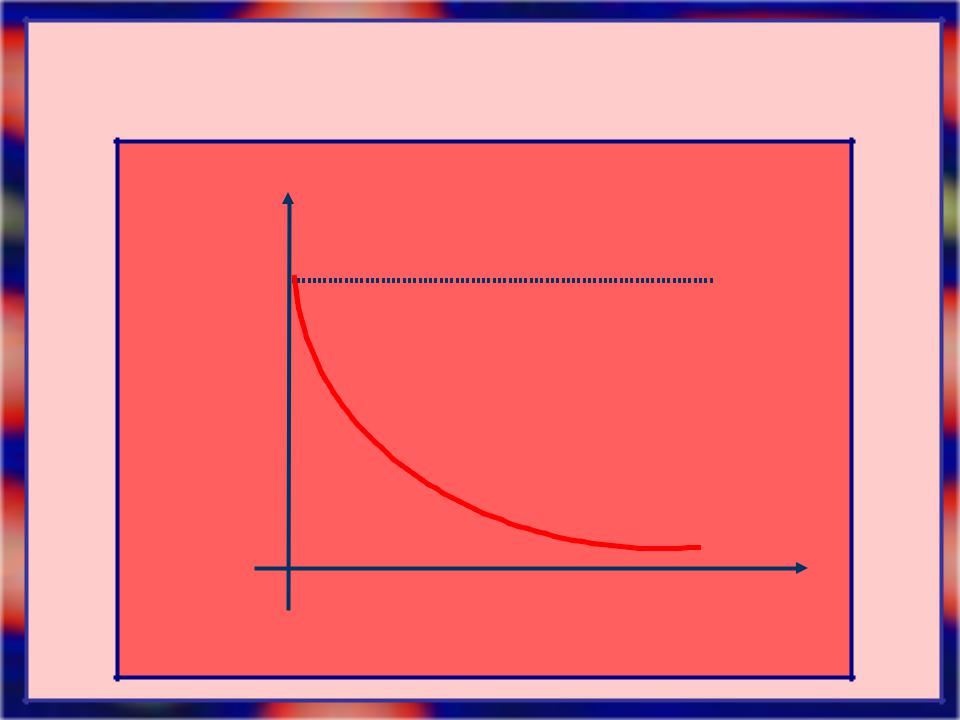
Кривая распределения имеет вид: |
f (x) |
|
x |
Найдем математическое ожидание и дисперсию случайной величины, распределенной по показательному закону.
|
|
M[ X ] x f (x)dx x e xdx |
|
|
0 |
Вынесем константы за знак интеграла и перейдем от несобственного интеграла к определенному, стоящему под знаком предела:
|
|
A |
x e xdx lim |
x e xdx |
|
|
A |
|
0 |
|
0 |
Полученный определенный интеграл будем брать по частям:
|
u x |
|
dv e xdx |
|
|
|
|
|
|
||||||||||||||||
|
du dx |
v |
|
|
|
1 |
|
e x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
x |
|
A |
|
|
A |
|
|
|
1 |
|
x |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
lim |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
dx |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x |
|
|
|
|
|
A |
1 |
|
|
|
|
A |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim |
|
|
|
e x |
|
|
|
|
|
|
|
|
e |
x |
|
|
|
||||||||
|
|
|
2 |
|
|
|
|||||||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A |
|
A |
|
1 |
|
A |
|
1 |
|
|
1 |
lim |
|
|
e |
|
|
|
e |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||||
A |
|
|
|
|
|
|
|
|
|
0 0
Первые два слагаемых в пределе равны 0, т.к. экспонента в минус бесконечной степени стремиться к 0.
Теперь найдем дисперсию.
D[ X ] M[ X 2 ] mx2
|
|
M[ X 2 ] x2 f (x)dx x2 e xdx |
|
|
0 |
Как и в предыдущем случае, переходим к пределу определенного интеграла:
A
lim x2 e xdx
A 0
Берем интеграл по частям:
u x2 dv e xdx
du 2xdx |
v |
1 |
e x |
|
|||
|
|
|
|
|
x |
2 |
|
A |
A |
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|||||||||
lim |
|
e x |
|
|
|
|
x e xdx |
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
0 |
|
|
|
||||||
|
|
|
|
|
||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
Полученный интеграл еще раз берем по частям:
|
|
|
u x |
|
dv e xdx |
|
|
|
|
|
|
|||||||||
|
|
|
du dx |
v |
1 |
e x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
A |
2 |
|
x |
|
|
A |
A |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
|
e x |
|
|
|
e x |
|
|
|
|
e xdx |
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
|
|
|
0 |
|
0 |
|
|
|||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
Полученный интеграл табличный:
|
|
x2 |
|
|
A |
|
2 |
|
|
x |
|
|
A |
|
1 |
|
A |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
|
|
e x |
|
|
|
|
|
|
|
e x |
|
|
|
|
e x |
|
|
|
|
|
2 |
|||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
Подставляем пределы интегрирования:
|
|
A2 |
|
A |
|
2 |
|
|
A |
|
A |
|
1 |
|
A |
|
1 |
|
2 |
|
lim |
|
|
e |
|
|
|
|
|
|
e |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Теперь находим дисперсию и среднеквадратичное отклонение:
D[ X ] |
2 |
|
1 |
|
1 |
|||||
2 |
2 |
2 |
||||||||
|
|
|
|
|
1 |
|
|
|||
x |
|
|
|
|
|
|||||
D[ X ] |
|
|||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||